Tangente à un cercle
En géométrie plane euclidienne, une tangente au cercle est une droite qui touche un cercle en un point unique, sans passer par l'intérieur du cercle. Les droites tangents aux cercles sont le sujet de nombreux théorèmes, et apparaissent dans de nombreuses constructions à la règle et au compas et des preuves. Une propriété souvent utilisée dans ces théorèmes est que la tangente en un point du cercle est orthogonale au rayon du cercle passant par le point de contact.
Tangentes à un cercle
Une droite tangente (t) à un cercle C intersecte le cercle en un point unique T, contrairement aux sécantes qui passent nécessairement par deux points du cercle. Cette propriété de tangence est conservée par de nombreuses transformations géométriques, comme les homothéties, les rotations, les translations, les inversions, et les projections. On dit que ces transformations conservent la structure d'incidence de la droite et du cercle, même si les images peuvent être déformées.
Le rayon d'un cercle est perpendiculaire à la tangente à son extrémité au bord du cercle. Réciproquement, la perpendiculaire au rayon passant par son extrémité est la tangente au cercle. La figure géométrique résultante du cercle et sa tangente montre une symétrie axiale le long du rayon.
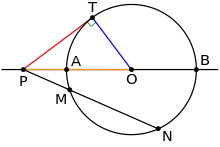
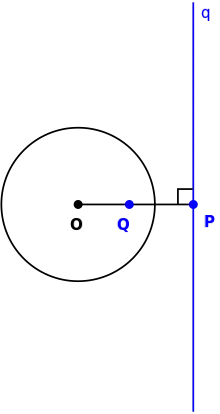
Aucune tangente ne passe par un point intérieur au cercle, car elle serait dès lors une sécante. Cependant, par un point extérieur P au cercle, il passe deux tangentes au cercle. La figure géométrique qui résulte de cette construction a une symétrie axiale le long de la droite passant par P et le centre du cercle. Ainsi, les longueurs des segments entre P et les points de tangence sont égaux. Par le théorème sécante-tangente, le carré de cette longueur de tangente est égale à la puissance du point par rapport au cercle. Cette puissance est égale au produit des distances de P à chacun des deux points d'intersection du cercle avec une sécante passant par P.
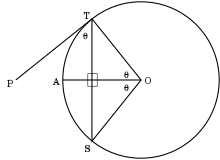
La droite tangente et le point de tangence ont une relation de conjugaison de l'un à l'autre, qui a été généralisé dans l'idée des pôles et polaires. La même relation réciproque existe entre un point extérieur au cercle et la sécante joignant les deux points de tangence.
Si un point P est extérieur au cercle de centre O, et si les tangentes issues de P touchent le cercle aux points T et S, alors ∠TPS et ∠TOS sont supplémentaires (leur somme vaut 180°).
Si une corde TM est tracée du point de tangence T vers le point extérieur P telle que ∠PTM ≤ 90° alors ∠PTM = (1/2)∠TOM.
Constructions au compas et à la règle non graduée
La construction d'une tangente t à un cercle de centre O, passant par le point T de sa circonférence au compas et à la règle non graduée est relativement directe :
- tracer la droite joignant O et T;
- la droite t est la perpendiculaire à (OT) passant par T
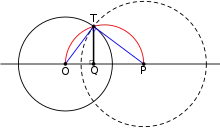
Le théorème de Thalès peut être utilisée pour construire les tangentes passant par un point P extérieur au cercle C :
- tracer un cercle centré au milieu du segment [OP], de diamètre OP
- les points d'intersection T1 et T2 du cercle C et du deuxième cercle sont les points de tangence des deux tangentes passant par P, selon ce qui suit.
Les segments OT1 et OT2 sont des rayons du cercle C ; comme ceux-ci sont inscrites dans un demi-cercle, ils sont perpendiculaires aux segments PT1 et PT2, respectivement. Mais une seule droite tangente est perpendiculaire au rayon. Ainsi, les deux droites depuis P et passant par T1 et T2 sont tangentes au cercle C.
Une autre méthode de construction des tangentes passant par un point P extérieur au cercle en utilisant que la règle non graduée :
- Tracer trois droites différentes passant par le point P qui coupent le cercle deux fois ;
- Soient A1, A2, B1, B2, C1, C2, les six points d'intersection, les deux points avec la même lettre se trouvant sur la même ligne, le point d'indice 1 est le plus proche de P ;
- Soit D le point d'intersection de A1B2 et A2B1 ;
- De même, soient E le point d'intersection de B1C2 et B2C1.
- tracer la droite (DE)
- les points d'intersection de (DE) sont les points de tangence recherchés[1]
Polygones circonscriptibles
Un polygone circonscriptible est un polygone dont chaque côté est tangent à un cercle particulier, son cercle inscrit. Tout triangle est circonscriptible ainsi que tout polygone régulier ; de plus, pour chaque nombre de côtés de polygone, il y a une infinité de polygones circonscriptibles non-isométriques.
Théorème des quadrilatères circonscriptibles et cercles inscrits
Un quadrilatère circonscriptible ABCD est un quadrliatère convexe dont les quatre côtés sont tangents à un cercle donné C. De façon équivalente, le cercle C est inscrit dans le quadrilatère ABCD. Par le théorème de Pitot, les sommes des longueurs des côtés opposés d'un tel quadrilatère sont égales :
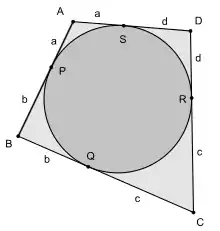
Cette conclusion suit l'égalité des segments tangents des quatre côtés d'un quadrilatère. On note les points de tangence P (sur le côté AB), Q (sur le côté BC), R (sur le côté CD) et S (sur le côté DA). Les segments tangents symétriques par rapport à chaque point de ABCD sont égaux : BP = BQ = b, CQ = CR = c, DR = DS = d et AS = AP = a. Mais chaque côté du quadrilatère est composé de deux tels segments tangents :
prouvant le théorème.
La réciproque est aussi vraie : un cercle peut être inscrit dans chaque quadrilatère dans lequel les sommes des longueurs des côtés opposés sont égales[2].
Ce théorème et sa réciproque ont plusieurs applications : on en déduit aussitôt qu'aucun rectangle n'est circonscriptible à moins que ce soit un carré, et qu'un losange a un cercle inscrit mais un parallélogramme n'en a pas dans le cas général.
Tangentes à deux cercles

Pour deux cercles extérieurs l'un de l'autre, il existe en général quatre droites distinctes qui sont tangentes aux deux cercles (bitangentes), mais dans certains cas particuliers, il peut y en avoir moins. Pour deux d'entre elles, les tangentes extérieures, les deux cercles sont du même côté de la ligne ; pour les deux autres, les tangents intérieures, les cercles sont de chaque côté. Les deux tangentes extérieures s'intersectent au centre d'homothétie externe, tandis que les deux tangentes intérieures s'intersectent au centre d'homothétie interne. Les deux centres d'homothétie et les centres des cercles sont alignés, le centre d'homothétie intérieure étant entre les deux centres des deux cercles et plus proche du centre du plus petit cercle, alors que le centre extérieur n'est pas entre les deux centres de cercle, mais à l'extérieur et du côté du centre du petit cercle. Si les deux cercles sont de même rayon, il y a toujours quatre bitangentes mais les tangentes extérieures sont parallèles et il n'existe pas de centre d'homothétie extérieur dans le plan affine ; dans le plan projectif, le centre d'homothétie extérieur est au point à l'infini correspondant à la pente de ces lignes[3].
Tangente extérieure
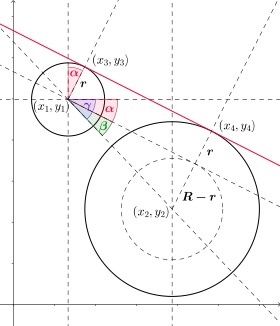
La ligne rouge joignant les points (x3 , y3) et (x4 , y4) est la tangente extérieure entre deux cercles. Avec les points donnés (x1 , y1), (x2 , y2), les points (x3 , y3), (x4 , y4) peuvent être aisément calculés avec l'angle α :
Ici R et r désignent les rayons des deux cercles et l'angle α peut être calculés par de la trigonométrie de base. On a en effet α = γ – β avec et [4].
Tangente intérieure
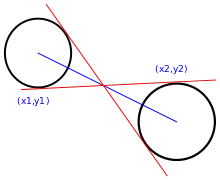
Une tangente intérieure est celle qui intersecte le segment joignant les deux centres des cercles. Cette droite ne peut être définie dans les cas où les cercles se croisent.
Construction
Les droites bitangentes peuvent être construites soit en construisant les centres homothétiques, comme montré dans cet article, puis en construisant les tangentes passant par ces centres, ou de façon plus directe. Ces méthodes ne fonctionnent pas dans les cas dégénérés, mais on peut les construire comme des cas limites.
Géométrie synthétique
Soient O1 et O2 les centres de deux cercles, C1 et C2, de rayons respectifs r1 et r2, avec r1 > r2 ; le cercle C1 est donc défini comme le plus grand des deux cercles. Il existe deux méthodes différentes pour construire les tangentes extérieures et intérieures.
- Tangentes extérieures
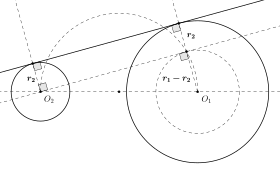
Un nouveau cercle C3 de rayon r1 − r2 est tracé, centré en O1. Par la méthode décrite ci-dessus, deux droites sont tracées depuis O2, tangentes à ce nouveau cercle. Ces droites sont parallèles aux tangentes recherchées, car la situation correspond à la réduction des deux cercles C1 et C2 par un taux constant, r2, qui réduit C2 à un point. Deux droites radiales peuvent être tracées depuis le centre O1 par les points de tangentes sur C3; ils intersectent C1 aux points de tangence désirés. Les droites tangentes extérieures recherchées sont les droites perpendiculaires aux droites radiales en ces points de tangence, qui peuvent être construites comme vu plus haut.
- Tangentes intérieures

Un nouveau cercle C3 de rayon r1 + r2 est tracé, centré en O1. Par la méthode décrite ci-dessus, deux droites sont tracées depuis O2, tangentes à ce nouveau cercle. Ces droites sont parallèles aux tangentes recherchées, car la situation correspond à la réduction de C2 à un point tout en agrandissant C1 par un taux constant, r2. Deux droites radiales peuvent être tracées depuis le centre O1 par les points de tangentes sur C3; ils intersectent C1 aux points de tangence désirés. Les droites tangentes intérieures recherchées sont les droites perpendiculaires aux droites radiales en ces points de tangence, qui peuvent être construites comme vu plus haut.
Géométrie analytique
Soient les cercles de centres c1 = (x1,y1) et c2 = (x2,y2) de rayons respectifs r1 et r2. En donnant l'équation d'une droite ax + by + c = 0, avec la normalisation a2 + b2 = 1, alors une bitangente aura pour équation :
Pour trouver , on commence par soustraire la première équation à la deuxième :
Si est la distance de c1 à c2, on peut normaliser par X = Δx/d, Y = Δy/d et R = Δr/d pour simplifier les équations, ce qui donne
La résolution donne deux solutions (k = ±1) pour les tangentes extérieures :
Géométriquement, cela correspond à calculer l'angle entre les tangentes et la droite des centres, puis l'utiliser pour faire pivoter l'équation de la droite des centres pour trouver l'équation de la tangente. L'angle est obtenu par le calcul des fonctions trigonométriques d'un triangle rectangle dont les sommets sont les centres d'homothétie (extérieurs), un centre d'un cercle, et un point tangent ; l'hypoténuse repose sur la tangente, le rayon est opposé à l'angle, le côté adjacent repose sur la droite des centres.
(X, Y) est le vecteur unité dirigé de c1 vers c2, tandis que R est cos θ où θ est l'angle entre la droite des centres et une tangente. sin θ est alors ± √1 – R2 (selon le signe de θ, ou l'angle de rotation), et les équations précédentes expriment la rotation de (X, Y) par ± θ, selon la matrice de rotation :
- k = 1 est la tangente à droite des cercles, vue de c1 vers c2.
- k = −1 est la tangente à gauche des cercles, vue de c2 vers c1.
On est resté ici dans le cas des rayons positifs. Si r1 est positif et r2 négatif, alors c1 va reposer à la gauche de chaque droite et c2 à leur droite, et les deux tangentes vont se croiser. Dans ce cas, on obtient les quatre solution. Echanger les signes de rayons inverse k = 1 et k = −1.
Vecteurs
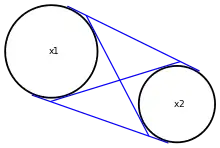
En général les points de tangence t1 et t2 pour les quatre droites tangentes aux deux cercles avec pour centres v1 et v2 et pour rayons r1 et r2 sont donnés en résolvant les équations vectorielles suivantes :
Ces équations expriment que la droite tangente, qui est parallèle à t2 – t1, est orthogonale au rayon, et que les points de tangence sont sur leurs cercles respectifs.
On obtient ainsi quatre équations quadratiques sur des vecteurs en dimension 2, ce qui donne en général quatre paires de solutions.
Cas dégénérés
Deux cercles distincts peuvent avoir entre zéro et quatre droites bitangentes, selon la configuration ; on peut séparer les cas selon la distance entre les centres et les rayons. En comptant avec leur multiplicité (une tangente commune étant compté deux fois) il y a donc zéro, deux ou quatre bitangentes. Des bitangentes peuvent être également généralisées en cercles, avec des rayons nuls ou négatifs. Les cas dégénérés et les multiplicités peuvent être comprises en termes de limites d'autres configurations – e.g., une limite de deux cercles qui se touchent presque, et en déplacer un pour qu'il y ait contact, ou un cercle avec un petit rayon qui se réduit à un point.
- si les cercles sont à l'extérieur l'un de l'autre (d > r1 + r2), ce qui est la position générale, il y a quatre bitangentes.
- s'ils se touchent en un point à l'extérieur (d = r1 + r2) – avec un point de tangence externe – il y a deux bitangentes extérieures et une bitangente interne, la tangente commune, donc de multiplicité 2, car les deux cercles sont de art en part de cette droite.
- si les cercles se croisent en deux points (|r1 – r2| < d < r1 + r2), alors il n'y a aucune bitangente intérieure et seulement deux bitangentes extérieures (elles ne peuvent ps être séparés car elles se croisent, donc pas de bitangente intérieure).
- si les cercles sont tangents intérieurement en un point (d = |r1 – r2|), alors il n'y a aucun bitangente intérieure et une bitangente extérieure double, la tangente commune.
- si un cercle est entièrement à l'intérieur (d < |r1 – r2|) alors il n'y a aucune bitangente, car une tangente au cercle intérieur devra forcément être sécant avec le cercle extérieur.
Si les deux cercles sont identiques, toute tangente est commune et donc bitangente aux deux cercles, donc tout point du cercle est un point de bitangence.
On peut étendre la notion de bitangence aux cercles de rayons négatifs (le même ensemble de points, x2 + y2 = (–r)2, mais considéré à l'envers), où dans ce cas si les rayons ont des signes opposés (un cercle a un rayon négatif et l'autre a un rayon positif) les centres d'homothétie extérieures et intérieures sont intervertis, tandis que si les rayons ont le même signe, "extérieure" et "intérieure" ont le même sens usuel (la double inversion permet de revenir au cas initial).
Les bitangentes peuvent également être définies quand un ou les deux cercles sont de rayon nul. Dans ce cas, les cercles de rayons nuls forment un point double, et toute droite passant par ce point le croise avec une multiplicité 2, et donc "tangent". Si un cercle est de rayon nul, une bitangente est simplement une droite tangente par le cercle est passant par le point, compté avec une multiplicité 2. Si les deux cercles sont de rayons nuls, la droite bitangente est la droite déinie par ces deux points, avec une multiplicité 4.
Notons que dans ces cas dégénérés, les centres d'homothétie extérieure et intérieure existent malgré tout en général (le centre extérieur est à l'infini si les rayons sont égales), sauf si les cercles coïncident, dans ce cas le centre extérieur n'est pas défini, ou si les deux cercles sont de rayons nuls, auquel cas le centre intérieur n'est pas défini.
Problème de la ceinture
Les tangentes intérieures et extérieures sont utiles pour la résolution du problème de la courroie, qui consiste à calculer la longueur d'une sangle ou d'une corde qui tiendra autour de deux poulies. En considérant la courroie comme une ligne mathématique d'épaisseur négligeable, et si les deux poulies sont placés sur le même plan, le problème revient à additionner les longueurs des segments de droites tangentes avec les longueurs d'arcs circulaires que parcourt la corde. Si la courroie est enroulée autour des roues et se croisent, les tangentes intérieures sont utiles. Réciproquement, si la ceinture est enroulée extérieurement autour des poulies, les tangentes extérieures apparaissent ; on parle parfois de "problèmes des poulies".
Droites tangentes à trois cercles : théorème de Monge
Pour trois cercles C1, C2 et C3, il y a trois paires de cercles (C1C2, C2C3, et C1C3). Comme chaque paire de cercles a deux centres homothétiques, il existe six centres homothétiques au total. Gaspard Monge a montré au début du XIXe siècle que ces six points sont sur quatre droites, chacune comptant trois points alignés.
Problème d'Apollonius

Plusieurs cas particuliers du problème d'Apollonius impliquent de trouver un cercle tangent à une ou plusieurs droites. Le plus simple est de construire des cercles tangents à trois droites données (le problème LLL). Pour résoudre ce problème, le centre d'un tel cercle doit être sur la bissectrice de chaque paire de ces droites ; il y a deux droites bissectrices pour chaque intersection. Les intersections de ces bissectrices sont les centres des cercles solutions, qui sont donc le cercle inscrit et les trois cercles exinscrits.
Un problème d'Apollonius peut en général être transformé en un cas plus simple de cercle tangent à un cercle et deux droites parallèles (lui-même cas particulier du cas LLC). Pour accomplir ceci, il suffit d'agrandir deux des trois cercles donnés jusqu'à avoir presque contact tangent. Une inversion au point de tangence selon un cercle de rayon bien choisi transforme les deux cercles touchants en deux droites parallèles, et le troisième cercle donné en un autre cercle. Ainsi, les solutions peuvent être obtenues en glissant un cercle de rayon constant entre deux droites parallèles jusqu'à ce qu'il y ait contact avec le troisième cercle transformé. Une ré-inversion donne les solutions du problème original.
Généralisations
Le concept de droite tangente à un ou plusieurs cercles peut être étendu de plusieurs façons. D'abord, la relation de conjugaison entre points de tangence et droites tangentes peut être généralisées aux pôles et droite polaires, dans lesquelles les pôles peuvent être n'importe où, et plus seulement sur la circonférence du cercle. Ensuite, l'union de deux cercles est un cas spécial (réductible) de courbe quartique, et les tangentes extérieures et intérieures sont les bitangentes de cette courbe quartique. En général, une quartique a 28 bitangentes.
Une troisième généralisation revient à considérer des cercles tangents, plutôt que des droites tangentes ; une droite tangente peut être considéré comme un cercle tangent de rayon infini. En particulier, les tangentes extérieures à deux cercles sont des cas limites d'une famille de cercles qui sont tangentes intérieurement ou extérieurement aux deux cercles, tandis que les droites tangentes intérieures sont des cas limites d'une famille de cercles qui sont tangents intérieurement à l'un et extérieurement à l'autre [5].
En géométrie de Möbius ou géométrie de l'inversion, les droites sont vues comme des cercles passant par un point "à l'infini" et pour toute droite ou tout cercle, il y a une transformation de Möbius qui projette l'une sur l'autre. En géométrie de Möbius, la tangence entre une droite est un cercle devient un cas spécial de tangence entre deux cercles. Cette équivalence est étendue plus loin en géométrie de la sphère de Lie.
Le rayon et la tangente sont perpendiculaires à un point du cercle, et orthogonale hyperbolique en un point de l'hyperbole unité. La représentation paramétrique de l'hyperbole unité par un vecteur radiant est p(a) = (cosh a, sinh a). La dérivée au point p(a) dans la direction de tangence la droite tangente en p(a), et vaut Le rayon et la tangente sont orthogonales hyperboliques en a car p(a) et sont images l'un de l'autre à l'asymptote y = x de l'hyperbole unité. Vu comme des nombres complexes déployés (où j j = +1), les deux nombres vérifient
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Tangent lines to circles » (voir la liste des auteurs).
- (en) « Finding tangents to a circle with a straightedge », sur Stack Exchange,
- (en) Alexander Bogomolny, « When A Quadrilateral Is Inscriptible? », sur Cut-the-knot
- (en) Paul Kunkel, « Tangent circles », Whistleralley.com (consulté le )
- (en) Shlomo Libeskind, Euclidean and Transformational Geometry: A Deductive Inquiry, , 110–112 p. (online copy sur Google Livres)
- (en) Paul Kunkel, « The tangency problem of Apollonius: three looks », BSHM Bulletin: Journal of the British Society for the History of Mathematics, vol. 22, no 1, , p. 34–46 (DOI 10.1080/17498430601148911, lire en ligne)


















