Bitangente
En géométrie, une bitangente à une courbe C est une droite L qui touche C en deux points distincts P et Q, et avec la même direction que C en ces points. Ainsi, L est la tangente à la courbe à la fois en P et Q.
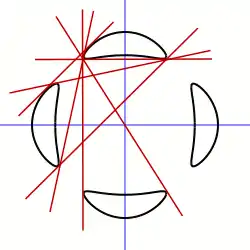
Bitangentes de courbes algébriques
En général, une courbe algébrique aura une infinité de droites sécantes mais un nombre fini de bitangentes.
Le théorème de Bézout implique qu'une courbe plane avec une bitangente doit être au moins de degré 4, elle en aura alors exactement 28, exactement 16, ou au plus 8. Le cas des 28 bitangentes d'une quartique (en) était un résultat célèbre de la géométrie du XIXe siècle, relié aux 27 droites sur une surface cubique.
Bitangentes de polygones
Les quatre bitangentes de deux polygones convexes disjoints peuvent être trouvés efficacement par un algorithme basé sur la recherche binaire dans lequel on maintient un pointeur binaire de recherche dans la liste des sommets de chaque polygone et déplace un des pointeurs à gauche ou à droite selon les lieux où les tangentes aux sommets aux deux pointeurs se croisent. Ce calcul de bitangente est une sous-routine clé en structure de données pour maintenir des enveloppes convexes dynamiquement (Overmars et van Leeuwen 1981). txt décrit un algorithme pour lister efficacement tous les segments de bitangentes qui ne croisent aucune des autres courbes dans un système de courbes convexes disjointes, par une technique basée sur la pseudotriangulation (en).
Les bitangentes peuvent être utilisés pour accélérer l'approche du graphe de visibilité pour la résolution du problème de plus court chemin euclidien : le plus court chemin entre un ensemble d'obstacles polygonaux qui ne peuvent que suivre ou quitter la frontière d'un obstacle le long de ses bitangentes, donc le plus court chemin peut être trouvé par l'algorithme de Dijkstra par un sous-graphe du graphe de visibilité formé par les sommets de visibilité qui reposent sur les droites bitangentes (Rohnert 1986).
Concepts reliés
Une bitangente diffère d'une sécante dans le sens où une droite sécante peut croiser la courbe au deux points où elle l'intersecte. On peut aussi considérer des bitangentes qui ne sont pas des droites ; par exemple, l'ensemble de symétrie (en) d'une courbe est le lieu des centres de cercles tangents à la courbe en deux points.
Les bitangentes à des paires de cercles apparaissent dans les travaux de Jakob Steiner en 1826 pour les cercles de Malfatti, dans le problème de la courroie pour calculer la longueur d'une courroie liant deux poulies, dans le théorème de Casey caractérisant des ensembles de quatre cercles avec un cercle tangent commun, et dans le théorème de Monge sur la colinéarité des points d'intersection de certaines bitangentes.
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Bitangent » (voir la liste des auteurs).
- (en) M. H. Overmars et J. van Leeuwen, « Maintenance of configurations in the plane », Journal of Computer and System Sciences, vol. 23, no 2, , p. 166-204 (DOI 10.1016/0022-0000(81)90012-X, hdl 1874/15899
 ).
). - (en) Michel Pocchiola et Gert Vegter, « The visibility complex », International Journal of Computational Geometry and Applications, vol. 6, no 3, 1996a, p. 297-308 (DOI 10.1142/S0218195996000204, lire en ligne [archive du ], consulté le ).
- (en) Michel Pocchiola et Gert Vegter, « Topologically sweeping visibility complexes via pseudotriangulations », Discrete and Computational Geometry, vol. 16, no 4, 1996b, p. 419-453 (DOI 10.1007/BF02712876).
- (en) H. Rohnert, « Shortest paths in the plane with convex polygonal obstacles », Information Processing Letters, vol. 23, no 2, , p. 71-76 (DOI 10.1016/0020-0190(86)90045-1).
- (en) Eric W. Weisstein, « Bitangent », sur MathWorld