Problème de la courroie
Le problème de la courroie est un problème mathématique qui consiste à trouver la longueur d'une courroie croisée qui relie deux poulies circulaires de rayon r1 et r2 dont les centres sont distants d'une longueur P. La solution du problème de la courroie utilise des résultats de trigonométrie et les notions de droite bitangente, et d'angles égaux.
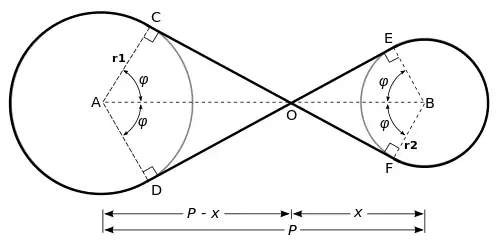
Résolution
Il est clair que les triangles ACO et ADO sont des triangles rectangles isométriques, de même que les triangles BEO et BFO. De plus, les triangles ACO et BEO sont semblables. Donc les angles CAO, DAO, EBO et FBO sont tous égaux. En désignant cet angle par (mesuré en radians), la longueur de la ceinture est
Cela exploite la propriété commode de désigner les angles en radians de sorte que la longueur d'un arc = le rayon × la mesure de l'angle faisant face à l'arc.
Pour trouver , on voit par la similitude des triangles ACO et BEO que
Pour P fixé, la longueur de la courroie ne dépend que de la somme des rayons r1 + r2, et non de leurs valeurs individuelles.
Problème de la poulie
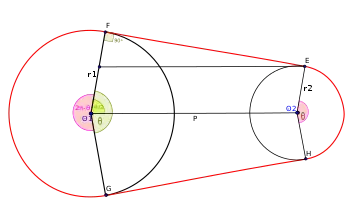
Il existe d'autres types de problèmes similaires au problème de la courroie. Le problème de la poulie, comme illustré, est similaire au problème de la courroie à la différence que dans ce problème, la courroie n'est pas croisée. Dans le problème de la poulie, la longueur de la courroie est
où r1 est le rayon de la plus grande poulie, r2 celui de la plus petite, et la valeur de donnée par :
Applications
Le problème de la courroie est utilisé [1] dans la conception des avions, des engrenages de vélo, des voitures et d'autres objets avec des poulies ou des courroies qui se croisent. Le problème de la poulie est également utilisé dans la conception des tapis roulants que l'on trouve dans les tapis à bagages des aéroports et les lignes d'usine automatisées[2].
Voir également
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Belt problem » (voir la liste des auteurs).
- Trigonometry examples in real life « https://web.archive.org/web/20090425071917/http://www.brainmass.com/homework-help/math/trigonometry/77582 »(Archive.org • Wikiwix • Archive.is • Google • Que faire ?),
- Trigonometry used in conveyor belts « https://web.archive.org/web/20120222193004/http://www.beltbrake.com/tech.htm »(Archive.org • Wikiwix • Archive.is • Google • Que faire ?),









