Cercles de Malfatti

Le problème de la construction de trois cercles tangents les uns aux autres dans un triangle avait déjà été posé avant les travaux de Malfatti par le mathématicien japonais du XVIII^e siècle Ajima Naonobu, dans une collection non publiée de ses œuvres réalisée un an après sa mort par son élève Kusaka Makoto[3] - [4]. Encore plus tôt, le même problème avait été considéré par Gilio di Cecco da Montepulciano dans un manuscrit de 1384 conservé à la Bibliothèque municipale de Sienne en Italie. Jacques Bernoulli a étudié en 1744 le cas particulier du triangle isocèle[5].

Depuis les travaux de Malfatti, il y a eu une quantité importante de travaux sur les méthodes de construction de ses trois cercles ; Richard K. Guy écrit que la littérature sur le problème est « abondante, largement dispersée et pas toujours consciente d'elle-même »[6]. Notamment, Jakob Steiner a présenté une construction géométrique utilisant les tangentes communes à des cercles ; d'autres auteurs ont depuis affirmé que la présentation de Steiner manquait de preuve, laquelle a ensuite été fournie par Andrew Hart [7], mais Guy signale que la preuve est en fait éparpillée dans deux articles de Steiner publiés à cette époque [6]. Des solutions basées sur des formulations algébriques du problème ont été données par Ludolph Lehmus en 1819 [8], Catalan en 1846 [9], C. Adams (en) en 1849 [10], J. Derousseau en 1895 [11], et Andreas Pampuch en 1904 [12]. Le problème et ses généralisations ont fait l'objet de nombreuses autres publications mathématiques du XIX^e siècle, et son histoire et ses mathématiques ont fait l'objet d'études continues depuis lors. Il a également été un sujet fréquent dans les livres de géométrie (par exemple dans la Géométrie de Rouché et Comberousse, 7^e édition, 1^er volume, p. 311 à 314) [13].

Construction par Steiner des cercles de Malfatti.

Bien qu'une grande partie des premiers travaux sur les cercles de Malfatti utilisaient la géométrie analytique, Steiner a proposé en 1826 la construction de géométrie pure, effectuable à la règle et au compas, suivante [14].

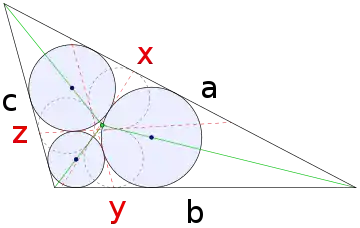
Un cercle tangent à deux côtés d'un triangle, comme le sont les cercles de Malfatti, doit être centré sur l'une des bissectrices internes du triangle (en vert sur la figure). Ces bissectrices divisent le triangle en trois triangles plus petits, et la construction par Steiner des cercles de Malfatti commence par celle des cercles inscrits dans ces triangles (représentés en pointillés sur la figure). Sauf cas particulier, ces cercles sont disjoints, et chaque paire de cercles possède deux tangentes communes passant entre les deux cercles : l'une est une bissectrice du triangle et l'autre est représentée par une ligne pointillée rouge dans la figure. Avec les notations de la figure, les trois cercles de Malfatti sont les cercles inscrits dans les trois quadrilatères abyx, aczx et bczy. En cas de symétrie, deux des cercles en pointillés peuvent être tangents en un point d'une bissectrice, qui est alors l'unique tangente commune située entre les cercles mais établissant toujours les quadrilatères de construction des cercles de Malfatti.

Les trois tangentes communes x, y et z coupent les côtés du triangle au point de tangence avec le troisième cercle inscrit, et peuvent également être obtenues comme symétriques des bissectrices du triangle par rapport aux droites reliant deux centres de ces cercles inscrits.

Des formules apparentées aux précédentes peuvent être utilisées pour trouver des exemples de triangles dont les longueurs des côtés, le rayon du cercle inscrit et les rayons de Malfatti sont tous entiers. Par exemple, le triangle de côtés de longueurs 28 392, 21 000 et 25 872 a un cercle inscrit de rayon 6 930 et pour rayons de Malfatti 3 969, 4 900 et 4 356. De même, le triangle de côtés de longueurs 152 460, 165 000 et 190 740 a un cercle inscrit de rayon 47 520 et pour rayons de Malfatti 27 225, 30 976 et 32 400 [17].

Construction du premier point de Ajima-Malfatti

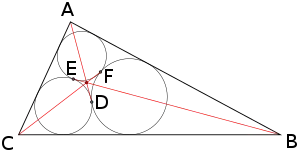
Étant donné un triangle ABC et ses trois cercles de Malfatti, soient D, E et F les points de tangence de deux des cercles, opposés aux sommets A, B et C respectivement. Les trois droites (AD), (BE) et (CF) concourent en un centre du triangle connu sous le nom de premier point de Ajima-Malfatti, honorant les contributions de Ajima et Malfatti. Le deuxième point de Ajima-Malfatti est le point de concours des trois droites reliant les points de tangence des cercles de Malfatti aux centres des cercles exinscrits du triangle (ces centres ont pour nombres de Kimberling X(179) et X(180)[18]).

D'autres centres du triangle sont associés aux cercles de Malfatti : le point de Yff-Malfatti, formé de la même manière que le premier point de Ajima-Malfatti à partir de trois cercles mutuellement tangents qui sont tous tangents aux droites passant par les côtés du triangle donné, mais qui se trouvent partiellement à l'extérieur du triangle (nombre de Kimberling X(400)) et le centre radical des trois cercles de Malfatti (le point de concours des trois bitangentes utilisées dans la construction, de nombre de Kimberling X(483)[18]).

Les 2 tangentes communes externes à chacun de 3 cercles deux à deux tangents extérieurement déterminent ${\displaystyle 2^{3}=8}$ triangles (rouge-vert-bleu) ayant pour cercles de Malfatti (à 9 contacts simples) généralisés ces 3 cercles. Si l'on rajoutait les tangentes communes internes, il y aurait alors ${\displaystyle 3^{3}=27}$ triangles [19].

Dans une résolution algébrique des équations donnant les cercles de Malfatti, on ne fait pas la distinction entre les tangences internes et externes entre les cercles et le triangle ; si le problème est généralisé pour permettre ces tangences, avec des points de contact simples (six points de contact cercle/côté, et trois points de contact cercle/cercle), un triangle donné possède 32 solutions différentes [19] - [15] - [11] - [12] - [16], et inversement un triplet de cercles mutuellement tangents est une solution pour huit triangles différents (voir ci-contre) [6]. Bottema [20] attribue l'énumération de ces solutions à Pampuch [12], mais Cajori [21] note que ce comptage du nombre de solutions était déjà donné dans une remarque de Steiner [2], lui-même faisant référence à une note publiée dans les Annales de Gergonne en 1810 [19].

Voici, dans le cas du triangle équilatéral, ces 32 solutions, à symétries près ; Barisien [15] ne retient que les 20 premières, présentant un axe de symétrie.

• 2 solutions à trois axes de symétrie (les rayons des cercles indiqués sont donnés pour un triangle de côté 1) [22]:

• 
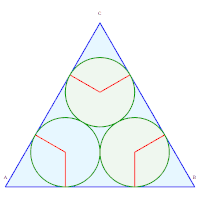  1. Rayons ${\displaystyle ({\sqrt {3}}-1)/4}$
• 
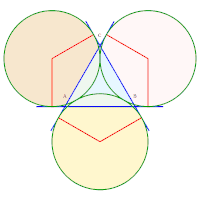  2. Rayons ${\displaystyle ({\sqrt {3}}+1)/4}$

• 18 = 6 x 3 solutions à un axe de symétrie [22]:
  • 
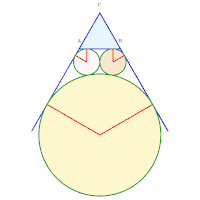    3, 4, 5. Rayons ${\displaystyle (5{\sqrt {3}}+9)/12,(3-{\sqrt {3}})/4}$
  • 
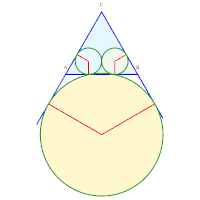    6, 7, 8. Rayons ${\displaystyle (3{\sqrt {3}}+5)/12,({\sqrt {3}}-1)/4}$
  • 
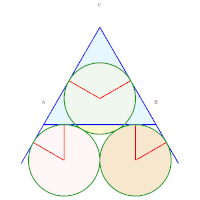    9, 10, 11. Rayons ${\displaystyle (3-{\sqrt {3}})/4}$
  • 
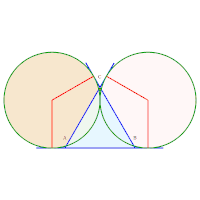    12, 13, 14. Rayons ${\displaystyle (2-{\sqrt {3}})/6,({\sqrt {3}}+1)/4}$
  • 
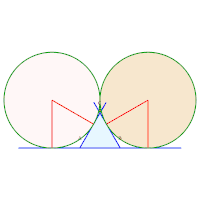    15, 16, 17. Rayons ${\displaystyle (9-5{\sqrt {3}})/12,({\sqrt {3}}+3)/4}$
  • 
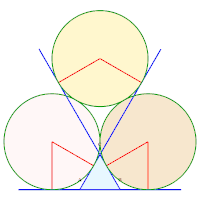    18, 19, 20. Rayons ${\displaystyle ({\sqrt {3}}+3)/4}$

• 12 = 2 x 6 solutions sans axe de symétrie [22]:

• 
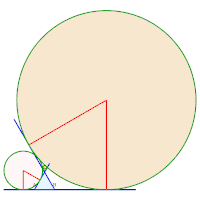  21 à 26.
• 
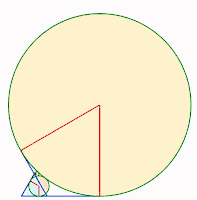  27 à 32.

Il existe aussi des solutions avec des points de contact multiples (Guy[6] en mentionne 48) :

• 
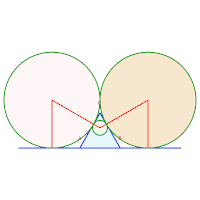  Exemple avec 2 contacts triples (deux cercles et un côté), 3 contacts simples.
• 
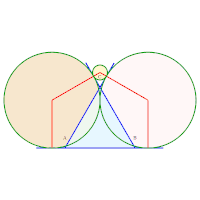  Idem.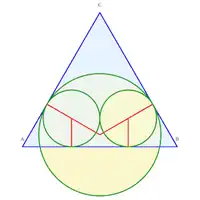
• 
  Idem, avec deux cercles tangents intérieurement au troisième.
• 
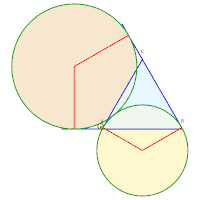  Exemple avec 1 contact triple et 6 simples.

• Empilement de cercles dans un triangle équilatéral
• Empilement de cercles dans un triangle isocèle rectangle
• Théorème des six cercles

• Cercles de Malfatti généralisés

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Malfatti circles » (voir la liste des auteurs).