Courbe quartique
En géométrie, une courbe quartique est une courbe algébrique de degré quatre.
Elle peut être définie par une équation de degré quatre :
Cette équation a quinze constantes. Cependant, elle peut être multipliée par une constante non nulle sans changer la courbe. De ce fait, l'espace des courbes quartiques peut être identifié avec l'espace projectif réel . Il en résulte qu'il y a exactement une seule courbe quartique qui passe par un ensemble de quatorze points distincts en position générale, puisqu'une quartique a 14 degrés de liberté.
Une courbe quartique peut avoir un maximum de :
- quatre composantes connexes,
- vingt-huit bitangentes (en),
- trois points doubles ordinaires, à moins qu'elle ne se décompose.
Un exemple de courbe quartique (gauche) est la fenêtre de Viviani.
On distingue plusieurs familles de quartiques en fonction du genre.
- Si le genre = 0, alors ce sont les quartiques rationnelles
- Si le genre = 1, alors ce sont les quartiques elliptiques
- Si le genre = 2, alors ce sont les quartiques du diable
- Si le genre = 3, alors ce sont les quartiques de genre trois
Exemples
- Courbe bicorne (en)
- Ovale de Descartes
- Ovale de Cassini
- Courbe deltoïde
- Lemniscate de Booth (hippopède de Proclus)
- Lemniscate de Bernoulli
- Besace et son cas particulier, la Lemniscate de Gerono
- Spirique de Persée
- Section torique
- Kampyle d'Eudoxe (en)
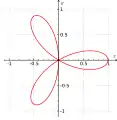
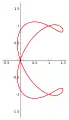 Courbe esperluette
Courbe esperluette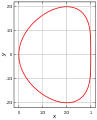 Courbe haricot
Courbe haricot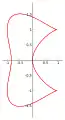 Courbe bicuspide
Courbe bicuspide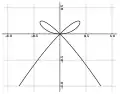 Courbe nœud
Courbe nœud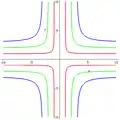 Courbes cruciformes
Courbes cruciformes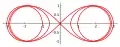
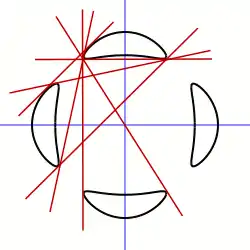 Courbe de Trott et quelques-unes des 28 bitangentes.
Courbe de Trott et quelques-unes des 28 bitangentes.
Liens externes
- Robert Ferréol, « Quartique », sur Encyclopédie des formes mathématiques remarquables
- Robert Ferréol, « Quartique bicirculaire », sur Encyclopédie des formes mathématiques remarquables
(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Quartic plane curve » (voir la liste des auteurs).
Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.

