Ovale de Descartes

Dans le cas d'un ovale non dégénéré, en prenant pour origine O le barycentre de F₁ et F₂ affectés des coefficient b² et –a² et pour ${\displaystyle {\vec {i}}}$ le vecteur tel que F₁ a pour abscisse α = a² . Alors F₂ a pour abscisse β = b² . En posant γ = c², l'équation de l'ovale devient[9] : ${\displaystyle (x^{2}+y^{2}-\sigma _{2})^{2}+8\sigma _{3}x-4\sigma _{1}\sigma _{3}=0}$ où σ₁, σ₂ et σ₃ sont les fonctions symétriques des réels α, β et γ : ${\displaystyle \sigma _{1}=\alpha +\beta +\gamma ,\quad \sigma _{2}=\alpha \beta +\beta \gamma +\gamma \alpha ,\quad \sigma _{3}=\alpha \beta \gamma }$

Le caractère symétrique des rôles joués par les réels α, β et γ permet de dire que la même équation cartésienne sera obtenue pour l'ovale de foyers F₁ et F₃(γ, 0) et d'équation |cMF₁ ± aMF₃| = |bF₁F₃| ainsi que pour l'ovale de foyers F₂ et F₃ et d'équation |cMF₂ ± bMF₃| = |aF₁F₃|.

On peut aussi décider de prendre pour origine, le milieu du segment [F₁F₂][10] ou un des foyers[11] pour obtenir des équations alternatives.

Dans le repère de centre F₁ et dont l'axe principal est orienté vers F₂, si l'on note d=F₁F₂, l'ovale complet d'équation |bMF₁ ± aMF₂| = |cF₁F₂| a pour équation polaire[12] :

${\displaystyle (b^{2}-a^{2})\rho ^{2}-2\rho d(a^{2}\cos \theta +bc)+(c^{2}-a^{2})d^{2}=0}$

Puisque le produit des deux racines de cette équation est indépendant de θ, l'ovale complet est invariant par inversion[13] de centre F₁ et de rapport ${\displaystyle {\frac {(c^{2}-a^{2})d^{2}}{(b^{2}-a^{2})}}}$.

Si l'ovale n'est pas dégénéré, le troisième foyer F₃ est le barycentre des points F₁ et F₂ affectés des coefficient b² - c² et c² - a², et les deux autres équations de l'ovale sont |cF₂M ± bF₃M| = |aF₂F₃| et |aF₃M ± cF₁M| = |bF₃F₂|, voir à théorème de Stewart.

Les 4 sommets de l'ovale complet sont les barycentres des points F₁ et F₂ affectés des coefficients (b - c, a + c), (b - c, - a + c), (b + c, a - c), (b + c, -a -c).

Propriété de réfraction de l'ovale intérieur : le rayon issu de F₁ se réfracte pour passer par F₂.

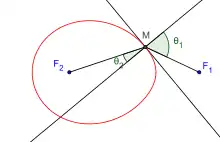
La normale à l'ovale d'équation bF₁M + aF₂M = cF₁F₂ au point M a pour vecteur directeur[8] : ${\displaystyle b{\frac {\overrightarrow {F_{1}M}}{F_{1}M}}+a{\frac {\overrightarrow {F_{2}M}}{F_{2}M}}}$

Ainsi, si on appelle θ₁ l'angle que fait F₁M avec la normale et θ₂ l'angle que fait F₂M avec la normale, on a l'égalité : ${\displaystyle {\frac {\sin \theta _{2}}{\sin \theta _{1}}}={\frac {b}{a}}}$.

Pour 0< b < a, on retrouve là, la loi de Snell-Descartes. Si l'ovale sépare deux milieux, l'un d'indice b contenant F₁ et l'autre d'indice a contenant F₂ et si M est le premier point de rencontre de la demi-droite [F₁M) avec l'ovale, alors le rayon F₁M) se réfracte en MF₂

Ovale d'équation 4F₁M ± 3F₂M = ± 2F₁F₂ construit grâce au point C, barycentre des points F₁ et F₂ affectés des coefficients -3 et 4, et aux cercles de centre F₁ et F₂ et de rayons respectifs ³⁄₂F₁F₂ et ⁴⁄₃F₁F₂.

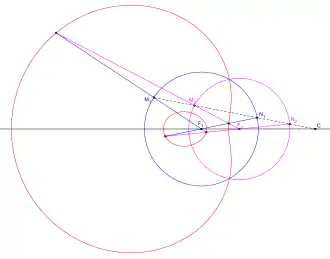
Michel Chasles[14] propose une construction d'ovale complet à l'aide de deux cercles de centres F₁ et F₂ et d'un point C situé sur la droite (F₁F₂). On fait pivoter une droite autour de C de telle sorte qu'elle rencontre le premier cercle en deux points M₁ et N₁ et le second cercle en M₂ et N₂. Les points de rencontre des droites (F₁M₁) et (F₁N₁) avec les droites (F₂M₂) et (F₂N₂) dessinent alors un ovale complet quand la droite pivote autour de C.

Projection orthogonale de l'intersection du cône de sommet S₁ avec le cône de sommet S₂ sur un plan perpendiculaire aux axes des cônes est un ovale de foyers S₁ et S₂.

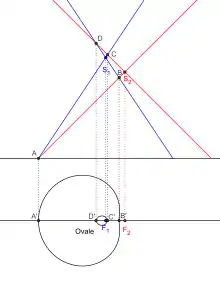
Un ovale de Descartes est le projeté vertical dans un plan horizontal de l'intersection de deux cônes de révolution d'axes verticaux différents. Les foyers sont alors les projetés des sommets des deux cônes. Cette interprétation permet de retrouver de façon relativement simple certaines propriétés géométriques des ovales[15]

Ovale de Descartes construit comme caustique secondaire du cercle de centre O et passant par P.

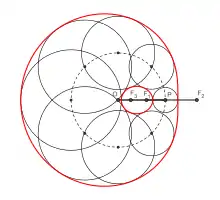
Si l'ovale complet a pour équation |bMF₁ ± aMF₂| = |cF₁F₂| et si les point O et P sont définis comme les barycentres de F₁ et F₂ affectés des coefficient b² et –a² pour O, et a et b pour P, l'ovale est alors la caustique secondaire par réfraction[16] de rapport n = |a/c| du cercle (Γ) de centre O, passant par P, par rapport au foyer F₁. C'est donc l'enveloppe des cercles (Γ_M) de centres M situés sur (Γ) et de rayons F₁M/n.

Chaque cercle (Γ_M) est tangent à l'ovale en deux points T_M et T'_M toujours alignés avec le troisième foyer de l'ovale[17].