Roulette (courbe)
En géométrie différentielle des courbes (en), une roulette est un type de courbe, une généralisation des cycloïdes, épicycloïdes, hypocycloïdes, trochoïdes, et courbes développantes.
Définition
Définition informelle
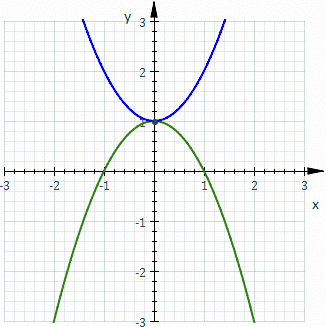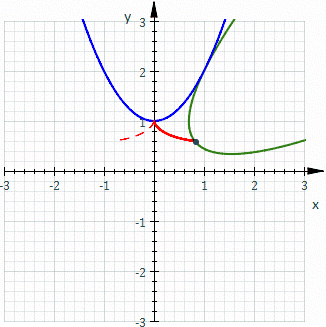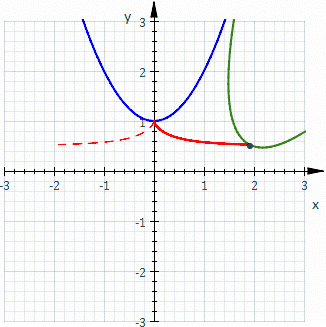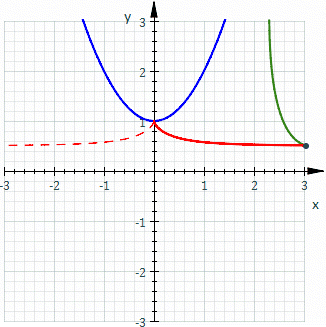
Grossièrement parlant, une roulette est une courbe décrite par un point (appelé « générateur » ou « pôle ») attaché à une courbe donnée qui elle-même roule sans glisser le long d'une seconde courbe (immobile). Plus précisément, étant donné une courbe « génératrice » dans un plan qui se meut de sorte que la courbe roule, sans glisser, le long d’une courbe directrice fixée à un plan occupant le même espace, alors le point attaché au plan mobile décrit une courbe, appelée roulette.
Dans l'illustration ci-contre, la courbe bleue (immobile) est une parabole, la courbe qui roule (en vert) est une parabole identique et le générateur est le sommet de la parabole mobile (qui décrit la roulette, en rouge). Dans ce cas, la roulette est une cissoïde de Dioclès.
Cas particuliers et notions liées
Lorsque la courbe qui roule est une ligne droite et que le générateur est un point sur cette ligne, la roulette est une développante de la courbe fixe. Si la courbe mobile est un cercle et la courbe fixe une droite alors la roulette est appelée trochoïde. Dans ce cas, si le point est fixé sur le cercle, il s'agit d’une cycloïde.
La glissette, courbe décrite par un point attaché à une courbe glissant le long de deux (ou plusieurs) courbes données est une notion proche.
Définition rigoureuse
D'un point de vue mathématique, il doit s’agir de courbes différentiables de l'espace euclidien. La courbe fixe reste invariante, la courbe roulante est soumise à une transformation congruente continue de sorte qu'à tout instant les courbes sont tangentes en un point de contact qui se meut à la même vitesse le long de chaque courbe. Une autre façon d’exprimer cette contrainte est de dire que le point de contact est le centre instantané de rotation de la transformation congruente. La roulette résultante est le lieu géométrique du générateur soumis à la même fonction congruente.
Modélisons les courbes dans le plan complexe. Soit deux paramétrisations naturelles des courbes () (roulante) et () (fixée), de sorte que , , et pour tout .
La roulette de générateur lorsque roule sur est donnée par l'application :
Généralisation
Si, à la place d’un seul point fixé à la courbe mobile, c'est une autre courbe qui est entraînée le long du plan mobile, une famille de courbes congruentes est produite. L'enveloppe de cette famille peut aussi être appelée roulette. Les roulettes dans des espaces de dimension supérieure peuvent être imaginées mais il faut aligner plus que des tangentes.
Exemple
Si la courbe fixe est une chaînette et la courbe roulante une droite,
La paramétrisation de la droite est choisie de telle sorte que :
En appliquant la formule précédente, on obtient :
Si p = −i, l'expression a une partie imaginaire constante −i et la roulette est une droite horizontale. Une application intéressante de ceci est qu'une roue carrée (en) peut rouler sans cahotement sur une route formée par une succession d'arcs de chaînettes.
Liste de roulettes
| Courbe fixe | Courbe mobile | Point générateur | Roulette |
|---|---|---|---|
| Courbe quelconque | Droite | Point sur la droite | Développante de la courbe |
| Droite | Cercle | Quelconque | Trochoïde |
| Droite | Cercle | Point sur le cercle | Cycloïde |
| Droite | Conique | Centre de la conique | Roulette de Sturm[1] - [2] |
| Droite | Conique (parabole/ellipse/hyperbole) | Foyer de la conique | Roulette de Delaunay[3] (chaînette/chaînette elliptique/chaînette hyperbolique)[4] |
| Droite | Épicycloïde ou hypocycloïde | Centre | Ellipse[5] |
| Cercle | Cercle | Quelconque | Trochoïde à centre (en) : épitrochoïde ou hypotrochoïde[6] |
| Cercle | Cercle | Point sur le cercle | Cycloïde à centre : épicycloïde ou hypocycloïde |
| Parabole | Même parabole paramétrée dans la direction opposée | Sommet de la parabole | Cissoïde de Dioclès[7] |
| Chaînette | Droite | Voir exemple ci-dessus | Droite |
Notes et références
- « Roulette de Sturm », sur mathcurve.com.
- Élastique rectangulaire si la conique est une hyperbole.
- « Roulette de Delaunay », sur mathcurve.com.
- (en) « Delaunay's roulette », sur 2dcurves.com.
- « Roulette à base rectiligne », sur mathcurve.com.
- « Trochoïde à centre », sur mathcurve.com.
- (en) « Cissoid », sur 2dcurves.com.
Voir aussi
Article connexe
Bibliographie
(en) W. H. Besant (en), Notes on Roulettes and Glissettes, Deighton, Bell & Co, coll. « Cornell University Historical Math Monographs », (lire en ligne)
Liens externes
- « Base, roulante et roulettes d'un mouvement plan sur plan », sur mathcurve.com
- (en) Eric W. Weisstein, « Roulette », sur MathWorld
- (en) « Roulette », sur 2dcurves.com
- (de) Roberta Aust, « Eine einheitliche Darstellung von ebenen, verallgemeinerten Rollbewegungen und deren Anwendungen », sur Beuth Hochschule für Technik Berlin (de),














