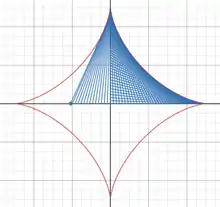
Glissette
En géométrie, une glissette est une courbe engendrée par le lieu géométrique d'un point ou par l'enveloppe d'une droite, d'un segment de droite ou d'une courbe attaché à une droite ou une courbe mobile glissant contre ou le long d'au moins deux droites ou courbes fixes. Le terme vient du mot glisser. Ci-dessous quelques exemples simples où les glissettes sont des cercles, des ellipses, des astroïdes ou des conchoïdes.
Cercle et ellipse
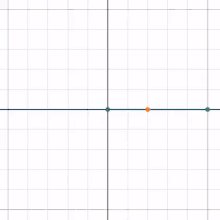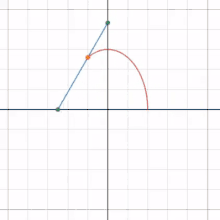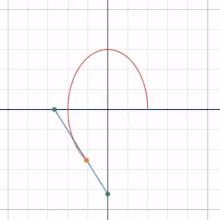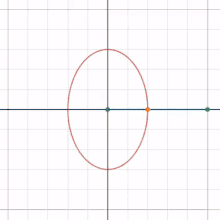
Un exemple de base est celui d'un segment de droite mobile dont les deux extrémités glissent le long de deux droites perpendiculaires fixes. Tous les points du segment de droite forme une ellipse sauf son milieu qui forme un cercle[1].
Conchoïde
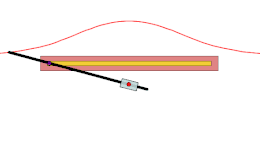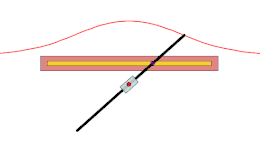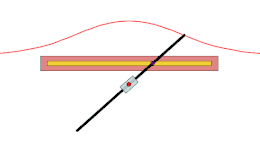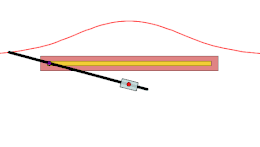
Tout conchoïde peut être considéré comme une glissette, avec une droite mobile et l'un de ses points glissant le long d'une droite et d'un point fixes[3].
Références
- William Besant, Notes on Roulettes and Glissettes, Deighton, Bell, (lire en ligne), p. 51
- Robert C. Yates, A Handbook on Curves and their Properties, Ann Arbor, MI, Edwards Bros., (lire en ligne), p. 109
- E. H. Lockwood, A Book of Curves, Cambridge University Press, (lire en ligne), p. 162