Courbe cycloïdale
Une courbe cycloïdale est une courbe plane transcendante, trajectoire d'un point fixé à un cercle qui roule sans glisser sur une courbe dite directrice. Il s'agit donc d'un cas particulier de roulette.
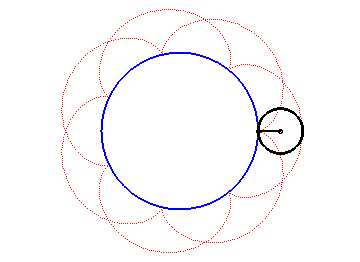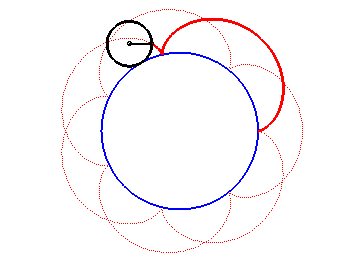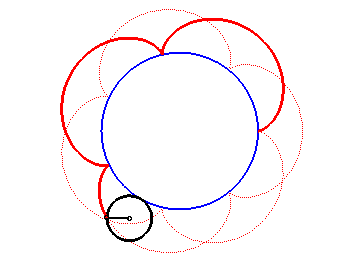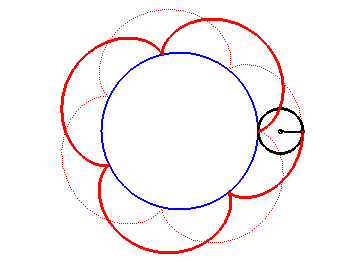
Construction d'une épicycloïde
Classification
Les différents cas particuliers de courbes cycloïdales sont liés à la forme de la directrice. Ainsi, on utilise les termes suivants :
- lorsque la directrice est un cercle, on parle de cycloïde à centre :
- lorsque le cercle roulant est à l'extérieur du cercle directeur, c'est une épicycloïde (dont la cardioïde et la néphroïde sont des cas particuliers) ;
- lorsque le cercle roulant est à l'intérieur du cercle directeur, c'est une hypocycloïde (dont la droite de La Hire, la deltoïde et l'astroïde sont des cas particuliers) ;
- lorsque la directrice est une droite, on parle de cycloïde droite ou tout simplement de cycloïde.
Définition mathématique
Une courbe cycloïdale peut être définie par deux équations intrinsèques:
où représente le rayon de courbure et l'abscisse curviligne On retrouve alors les cas particuliers évoqués ci-dessus :
- : cycloïde (A = 4 fois le rayon du cercle roulant)
- : épicycloïde ( où a est le rayon du cercle de base, b celui du cercle roulant)
- : hypocycloïde ( où a est le rayon du cercle de base, b celui du cercle roulant).
Voir aussi
Articles connexes
- Trochoïde : lorsque le point mobile n'est pas fixé sur le cercle roulant mais à l'extérieur ou à l'intérieur de celui-ci
- Cycloïde, § « Étymologie et histoire »
Lien externe
« Courbe cycloïdale », sur mathcurve.com
Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.
![{\displaystyle \left[1\right]\quad R_{c}^{2}+\omega ^{2}s^{2}=\omega ^{2}A^{2}}](https://img.franco.wiki/i/fe5a808cc43ff4ee9aab8c69fef11d3f92505ba2.svg)
![{\displaystyle \left[2\right]\quad s=A\sin(\omega \phi )\,}](https://img.franco.wiki/i/ecbe26aa4f072052e1854f1bad925f382b791d01.svg)






