Puissance en régime alternatif
La puissance en régime alternatif est la puissance dans un circuit électrique fonctionnant en régime alternatif sinusoïdal. Elle s'exprime de façon particulière en raison du caractère périodique des fonctions manipulées. Il est possible de déterminer plusieurs types de grandeurs homogènes à des puissances, ayant chacune une signification particulière.
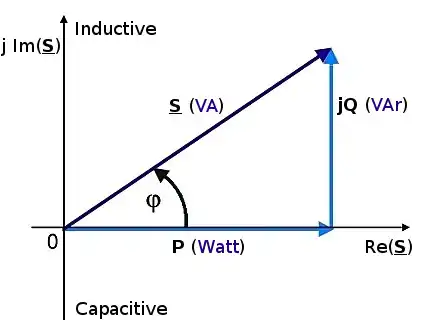
Puissance active (P, en watts (W))
Puissance réactive (Q, en voltampères réactifs (var))
Puissance apparente (S, en voltampères (VA))
Puissance active
La puissance active (ou puissance réelle) correspond à la puissance moyenne fournie au cours d'une période donnée. Notée , elle est exprimée en watts (W).
Pour un courant et une tension de période , son expression est :
Pour une tension sinusoïdale de valeur efficace et un courant sinusoïdal de valeur efficace déphasé d'un angle par rapport à la tension, cette expression devient :
En régime sinusoïdal, le rapport entre valeur maximale et efficace vaut (voir valeur efficace), correspond alors au facteur de puissance.
C'est la seule puissance à avoir un sens physique direct : par exemple dans le cas d'une résistance la puissance active est également la puissance thermique dissipée. Il n'y a pas de déphasage dans une résistance, donc et .
Puissance apparente
La puissance apparente en régime alternatif est le produit de la valeur efficace de la tension électrique aux bornes du dipôle par la valeur efficace du courant électrique traversant ce dipôle.
La puissance apparente se note et est exprimée en voltampères (VA).
La puissance apparente complexe est :
avec : nombre complexe conjugué de l'intensité complexe . La puissance apparente réelle est le module de la puissance apparente complexe. Autrement dit, on a :
- ,
étant la différence de phase entre la tension et le courant.
La puissance apparente est définie aussi bien en régime sinusoïdal que dans les autres cas de régimes alternatifs, mais les autres notions développées dans l'article n'ont de sens que dans le cas sinusoïdal.
Puissance réactive
En régime sinusoïdal, la puissance réactive est la partie imaginaire de la puissance apparente complexe. Elle se note , est exprimée en voltampères réactifs (var, voir le paragraphe « Unités ») et on a :
Les dipôles ayant une impédance dont la valeur est un nombre imaginaire pur (capacité ou inductance) ont une puissance active nulle et une puissance réactive égale en valeur absolue à leur puissance apparente.
Portée pratique
La puissance réactive apparaît dans tout système ayant des composants réactifs (c'est-à-dire capacitifs ou inductifs). Elle peut être soit « produite » (circuit capacitif) soit « consommée » (circuit inductif) par les différents éléments des circuits. Même si elle est imaginaire (au sens mathématique du terme), la puissance réactive a une signification physique réelle et sa valeur est essentielle au dimensionnement et à la stabilité des réseaux électriques (les lignes électriques étant elles-mêmes inductives).
Alors que la puissance active est utilisée pour générer un travail (par exemple celui d'un moteur) ou de la chaleur[1], la puissance réactive correspond, lorsqu'elle est « consommée », par exemple à l'établissement du champ magnétique dans les machines électriques (transformateurs, machine asynchrone, etc.)[2]. Parmi les consommateurs d'énergie réactive, on peut citer également : les lampes fluorescentes et à décharge à ballast magnétique, les moteurs et ascenseurs, les groupes frigorifiques, le chauffage par induction (fours à induction et à arc), les machines à souder[2] et les convertisseurs statiques[1].
Si la puissance réactive prélevée par les consommateurs est trop élevée par rapport à la puissance active, l'augmentation du courant dans tout le réseau électrique (réseau privé et réseau de distribution) entraine des pertes thermiques, des surcharges des transformateurs de distribution, l'échauffement des câbles d'alimentation et des chutes de tension, il est donc primordial d'y remédier[2]. Surdimensionner ces installations, avec les conséquences économiques que cela représente n'étant pas réaliste, il est préférable de compenser cette puissance réactive en améliorant le facteur de puissance[1], par l'installation de systèmes « produisant » de l'énergie réactive[2]. Ces systèmes peuvent être des condensateurs[1], des ensembles d'inductances et de condensateurs (ensembles qui peuvent être automatisés), des machines tournantes (compensateurs synchrones) ou des compensateurs statiques[2].
Mesure de la puissance
En France, la tarification des clients pour lesquels la livraison de l'énergie est faite en haute tension, le client assurant la transformation en basse tension par son propre transformateur privé, tient compte de l'énergie réactive[3]. L'énergie réactive consommée au-delà d'un seuil fixé à (à certaines heures entre novembre et mars) fait l'objet d'une facturation[3]. Le but de cette facturation est d'indemniser le transporteur de l'énergie pour les pertes causées sur son réseau, et c'est également une incitation pour les clients à améliorer leur installation (voir ci-dessus)[3]. La notion de est plus généralement exprimée par la valeur du facteur de puissance correspondant : [3].
Puissance déformante
En régime de tension sinusoïdale, un courant de forme périodique mais non purement sinusoïdal peut être décomposé en un courant fondamental de même fréquence que la tension et en une somme de courants harmoniques. La notion de puissance déformante permet de prendre en compte leur effets. Elle se note D et est exprimée en voltampères déformants (VAD)[4] - [5].
Calculs en régime sinusoïdal
En notant :
- puissance active ;
- puissance apparente ;
- puissance réactive .
Soit un dipôle linéaire dont l'impédance s'écrit : (R : partie réelle [la résistance], j : unité imaginaire, X : partie imaginaire [la réactance]), si l'on décompose le dipôle en deux dipôles en séries d'impédances respectives R et X (ils sont soumis au même courant I), on a :
Si l'on décompose le dipôle en deux dipôles en parallèles d'impédances respectives R' et X' (ils sont soumis à la même tension U), on a :
Avec et
est l'argument de et le module de .
La valeur de correspond au facteur de puissance en régime sinusoïdal. On a les relations :
- , d'où
- .
Unités
- L'unité de puissance active est le watt (W)
- La puissance apparente est quant à elle exprimée en voltampères, (VA).
- La puissance réactive s'exprime en voltampères réactifs (var).
La brochure du BIPM précise en marge du chapitre 2.3.4 Unités dérivées : « La Commission électrotechnique internationale (IEC) a introduit le var (symbole : var) comme symbole spécial pour l'unité de puissance réactive. Exprimé en unités SI cohérentes, le var est identique au volt-ampère[6] - [7].
Le var et le VA sont homogènes au Watt : on le remarque en voyant les formules passant de la puissance réactive à une des deux autres, sachant que le facteur de puissance est sans unité, ou simplement en analysant la formule . En fait, les unités diffèrent uniquement pour éviter d'additionner directement des puissances de différents types.
Intérêt de la notion
La méthode de Boucherot utilise les puissances réactive et apparente dans les calculs pour déterminer la puissance totale dans un circuit électrique.
D'autre part, ces puissances interviennent dans le dimensionnement d'un réseau électrique, et la puissance active n'est donc pas la seule à prendre en compte pour calculer les coûts[8].
Il faut également savoir qu'un générateur en alternatif, par exemple un onduleur, doit être capable non seulement de délivrer une puissance active au moins égale à la somme des puissances active de la charge qu'elle alimente, et il doit en être de même pour la puissance apparente.
Notes et références
- Patrick Abati, « La compensation de l'énergie réactive », sur sitelec.org, .
- « Schneider-electric : La compensation de l’énergie réactive » (consulté le ).
- « Compensation d’énergie réactive » [PDF], sur schneider-electric.fr (consulté le ).
- « Puissances en régimes périodiques – 1. Puissances – 4. Puissance déformante », sur physapp.tsetcholet.free.fr (consulté le ).
- Pierre Mayé, « Problèmes corrigés d’électronique de puissance », sur dunod.com, Éditions Dunod (consulté le ) [PDF].
- Le Système international d'unités (SI), Sèvres, Bureau international des poids et mesures, , 9e éd., 216 p. (ISBN 978-92-822-2272-0, lire en ligne [PDF]), p. 29.
- Le var et le VA selon la CEI : (en) SI units – Electricity and magnetism – Reactive power, Q – Apparent power, S.
- Sophie Deladreue, Patrick Bastard, Hugo Moreno, Patrick Sandrin, « Estimation du degré de concentration d'un éventuel marché de la puissance réactive et environnement concurrentiel », sur supelec.fr, Supélec, [PDF].





































