Problème de plus court chemin
En théorie des graphes, le problème de plus court chemin est le problème algorithmique qui consiste à trouver un chemin d'un sommet à un autre de façon que la somme des poids des arcs de ce chemin soit minimale.
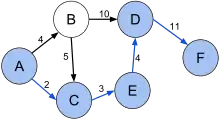
Variantes du problème du plus court chemin
Il existe de nombreuses variantes de ce problème suivant que le graphe est fini, orienté ou non, que chaque arc ou arête possède ou non une valeur qui peut être un poids ou une longueur. Un chemin le plus court entre deux nœuds donnés est un chemin qui minimise la somme des valeurs des arcs traversés. Pour calculer un plus court chemin, il existe de nombreux algorithmes, selon la nature des valeurs et des contraintes supplémentaires qui peuvent être imposées. Dans de nombreux cas, il existe des algorithmes de complexité en temps polynomiale, comme l'algorithme de Dijkstra dans des graphes avec poids positifs. En revanche, lorsque des contraintes supplémentaires comme des fenêtres de temps sont ajoutées, le problème peut devenir NP-difficile.
L'exemple d'application le plus courant est la recherche d'un trajet le plus court entre deux agglomérations. Ce problème d'apparence facile, puisqu'il s'agit simplement d'additionner les distances kilométriques, devient plus compliqué si on veut en déduire le temps de parcours, car l'intensité du trafic, le temps de traversée des agglomérations, sont des contraintes additionnelles. La recherche de chemin est au contraire un problème d'intelligence artificielle qui se rattache à la planification. Il consiste à trouver comment se déplacer dans un environnement entre un point de départ et un point d'arrivée en prenant en compte différentes contraintes. Il devient ardu lorsque diverses contraintes additionnelles (exécution en temps réel, présence d'incertitudes, contrainte de ressources, environnement évolutif, etc.) doivent être prises en compte.
Poids des arcs
Le problème et ses solutions dépendent d'abord de la nature des poids : chaque arc est doté d'un poids qui est un nombre réel. Les différents cas considérés sont :
- Les poids sont tous positifs : Dans ce cas, l'algorithme de Dijkstra permet de résoudre le problème du plus court chemin d'un sommet donné aux autres sommets en complexité en temps pour un graphe à arcs et sommets.
- Les poids sont quelconques, mais il n'y a pas de circuit de poids négatif (pas de circuit absorbant) : Dans ce cas, l'algorithme de Bellman-Ford permet de tester s'il existe un circuit absorbant et, en absence d'un tel circuit, de trouver un plus court chemin en temps .
- Les poids sont quelconques : Cette variante est NP-difficile, comme on peut le voir en considérant la réduction du problème du chemin hamiltonien NP-complet qui consiste à fixer le poids des arcs à .
Variantes du problème
On distingue essentiellement deux variantes du problèmes :
Recherche à partir d'un sommet donné (« Single source »)
On fixe un sommet , la source ou l'origine, et on cherche un chemin de longueur minimale de cette source à tous les sommets. Les algorithmes les plus importants sont
- L'algorithme de Dijkstra dans le cas de poids positifs
- L'algorithme de Bellman-Ford dans le cas de poids quelconques.
Des variantes sont :
- L'algorithme A* est un algorithme basé sur une heuristique pour la recherche entre deux points donnés.
- L'algorithme de Viterbi permet de corriger, dans une certaine mesure, les erreurs survenues lors d'une transmission à travers un canal bruité.
Le problème dual est la recherche d'un plus court chemin de tous les sommets vers un sommet commun (la cible). Ce problème se traite en inversant le sens des arcs.
Recherche pour tous les couples de sommets (« All pair »)
On cherche un plus court chemin, ou au moins la longueur d'un tel chemin, pour tous les couples de sommets.
- L'algorithme de Floyd-Warshall donne la matrice des longueurs des plus courts chemins en temps pour un graphe à sommets, mais le graphe ne doit pas posséder de circuit de poids strictement négatif. L'existence d'un circuit négatif se voit par des valeurs négatives sur la diagonale principale.
- L'algorithme de Johnson résout le problème en absence de circuit négatifs, et peut être plus rapide que Floyd–Warshall dans des graphes creux.
Formulation comme programme linéaire
Le problème du plus court chemin peut être formulé comme un problème d'optimisation linéaire comme suit.
Soit un graphe, avec deux sommets distingués (la source ou l'origine) et (le but ou le puits) ; on note le coût de l'arc . On considère le programme linéaire en les variables suivant
- minimiser
avec les contraintes et, pour tout i,
L'explication intuitive est que est une variable qui sert à indiquer si l'arc fait partie ou non du plus court chemin trouvé: elle vaut 1 si c'est le cas, et 0 sinon. On cherche à choisir l'ensemble d'arcs de poids total minimal, pourvu que les arcs composent un chemin de s à t ; cette condition est représentée par la contrainte qui exprime que, pour tout sommet autre que s et t, le nombre d'arcs entrants choisis doit être égal au nombre d'arcs sortant, et ainsi l'ensemble forme un chemin de s à t.
Le programme dual de ce programme linéaire est
- maximiser
avec les contraintes
- pour tout i,j.
Pour toute solution réalisable du dual, les coûts réduits sont non négatifs et sur ces coûts réduits, l'algorithme A* se comporte essentiellement comme l'algorithme de Dijkstra.
Une solution du programme dual est un potentiel aux nœuds nennt man ein Knotenpotential. On voit facilement que pour toute solution , le vecteur est aussi une solution pour tout . On peut en particulier choisir de sorte que . Ainsi la valeur à maximiser est .
Pour un chemin quelconque de à un sommet , la longueur peut être estimée
Ceci montre que le potentiel d'un nœud est une borne inférieure à la longueur d'un chemin. On trouve une solution optimale du programme dual en choisissant le potentiel d'un nœud comme la longueur du plus court chemin de à pour la fonction objectif .
Algorithme de Floyd-Warshall généralisé
La similitude entre l'algorithme de Warshall, l’algorithme de Floyd-Warshall et l'algorithme de McNaughton et Yamada s'explique par une structure algébrique sous-jacente, celle de demi-anneau. Cette interprétation a été présentée, en premier lieu, dans un article de Claude Pair en 1966[1], puis reprise dans un livre de Claude Pair et Jean-Claude Derniame[2]. La première version en anglais n’apparaît qu'en 1974 dans le livre d'Aho, Hopcroft et Ullman[3]. Elle est reprise ultérieurement, par Gondran et Minoux par exemple[4]; ces derniers citent un article français de 1968 de Pierre Robert et Jacques Ferland[5].
Un demi-anneau est un ensemble muni de deux lois binaires et . La loi est associative, commutative et admet un élément neutre noté 0 ou . La loi est associative et distributive par rapport à . Elle admet un élément neutre noté 1 ou . L'algèbre de Boole est un exemple de demi-anneau en prenant , (ou) et (et).
Pour que l'algorithme de Floyd-Warshall généralisé fonctionne, il faut de plus supposer que le neutre de la loi soit absorbant pour la loi . Autrement dit, pour tout élément du demi-anneau, l'égalité doit être vérifiée.
Matrice associée à un graphe pondéré
Soit donné un graphe dont les sommets sont . On associe à chaque arc un poids (une longueur, une distance, une densité de trafic selon le problème) qui est un élément d'un demi-anneau (demi-anneau plus ou moins simple selon la nature du problème à traiter). La matrice associée au graphe pondérée est la matrice dont l'élément en position est si l'arc existe, et égal à 0 (le du demi-anneau) sinon.
Le poids d'un chemin est le produit, dans le demi-anneau, des poids de arcs qui le composent :
- .
La longueur du plus court chemin de à est, dans ce formalisme la somme des poids de à . Si l'on note l'ensemble des chemins de à , le chemin cherché est un chemin dont le poids est
- .
Dans le cas où et , c'est le poids minimal d'un chemin reliant à .
Algorithme de Floyd-Warshall généralisé
Étant donné un graphe de matrice associée d'ordre , avec , on définit deux suites de matrices :
- une suite de matrices par :
- et
- avec .
- Cette suite de matrices est telle que l'élément de la matrice est égal à la somme des poids des chemins de longueur au plus de à .
- une autre suite de matrices par :
- Cette suite de matrices est telle que les éléments ont pour valeur l'indice du premier point intermédiaire du chemin de à à l'étape .
Il s'ensuit que est l'indice du premier sommet intermédiaire entre et , le second sommet est donné par où , etc.
Applications
Existence des chemins joignant des sommets
C'est le problème de savoir, pour tout couple de sommets, s'il existe un chemin de à , ou de connaître, pour un sommet donné, les sommets accessibles à partir de . Ce problème de fermeture transitive se formule en choisissant un même poids pour chaque arc.
On peut donc résoudre le premier problème par l'algorithme de Warshall, le deuxième aussi par un simple parcours, en profondeur ou en largeur, à partir du somme s.
Distance minimum entre deux sommets
La distance minimum pour toute paire de sommets se calcule par l'algorithme de Floyd-Warshall, donc en prenant le demi-anneau tropical ou (max,+)-demi-anneau sur les nombres réels positifs ou nuls.
Chemins à capacité de trafic maximale entre deux sommets
La capacité de trafic possible sur un chemin est le minimum des capacités des arcs qui composent le chemin. Le chemin de capacité maximale est celui qui maximise ce minimum. On calcule les valeurs par l'algorithme de Warshall généralisé, en prenant et .
Réseaux routiers
Un réseau routier peut être considéré comme un graphe avec des poids positifs. Les nœuds représentent des croisements de routes et chaque arc du graphe est associé à un segment de route entre deux croisements. Le poids d'un arc peut correspondre à la longueur du segment de route associé, au temps nécessaire pour traverser le segment ou au coût de parcours du segment. En utilisant des graphes orientés, il est également possible de modéliser des rues en sens unique. Ces graphes ont des propriétés particulières en ce sens que certains arcs sont plus importants que d'autres pour les voyages à longue distance (typiquement les autoroutes). Cette propriété a été formalisée en utilisant un paramètre supplémentaire appelé « Highway Dimension »[6]. Elle permet de calculer des chemins optimaux plus rapidement que dans les graphes généraux. L'idée première est que si on veut aller d'une petite ville à une autre, située assez loin, on a intérêt à chercher une grande ville près du lieu de départ, et une grande ville près de l'arrivée, et de combiner le chemin en passant par les deux grandes agglomérations.
Ces algorithmes travaillent en deux phases. Dans une première phase de prétraitement, le graphe est adapté pour permettre une interrogation rapide. La deuxième phase est la phase d'interrogation ; les nœuds de départ et d'arrivée sont alors connus, et comme le réseau est statique, le prétraitement peut être fait une fois pour toutes et être utilisé pour de nombreuses interrogations.
L'algorithme le plus rapide connu (en 2011) est appelé « hub labelling », et calcule les chemins les plus courts en quelques fractions de secondes[7]
Plus court chemin pour des poids dynamiques
Dans certains problèmes de transport, les poids sont des fonctions qui peuvent varier avec le temps pour tenir compte des fluctuations du trafic par exemple. Dans ce cas, la méthode algébrique s'applique toujours en choisissant comme demi-anneau le demi-anneau des endomorphismes croissants sur un dioïde, avec la somme induite , et la composition pour produit. Ainsi, si l'on cherche à trouver le chemin le plus rapide dans un réseau où le trafic est variable en fonction de l'heure de départ, on peut appliquer les algorithmes usuels en valuant chaque route par une fonction donnant l'heure d'arrivée en fonction de l'heure de départ, et en considérant pour le minimum d'une fonction prise à l'heure de départ.
Plus court chemin avec contraintes temporelles
Il arrive, en particulier dans les réseaux de transports en commun, que certains arcs ne puissent être parcourus que dans certaines contraintes horaires (pas la nuit par exemple). On suppose que le temps de parcours de chaque arc est fixé, ainsi qu'un ensemble de plages horaires où il est possible d'emprunter cette route. On considère alors le dioïde des endomorphismes pris sur les intervalles de temps définis ainsi : soit l'intervalle de temps où l'on souhaite partir du sommet ; alors est l'intervalle de temps où il est possible d'arriver au sommet relié à . On peut ajouter d'autres contraintes à (par intersection avec des plages horaires pour éviter certaines périodes, en ajoutant des contraintes de prix par produit cartésien avec la matrice des coûts de transport muni d'une loi min pondérée entre temps et prix). Dans tous les cas, l'algorithme de Dijkstra permet une résolution efficace.
Réseaux stochastiques avec contraintes temporelles
Dans des situations réelles, le réseau de transport est habituellement stochastique et dépend du temps. En effet, un voyageur qui parcourt un trajet quotidiennement peut connaître des temps de déplacement différents sur ce trajet en raison non seulement des fluctuations de l'intensité du trafic, mais aussi des incidents plus localisés tels que les zones de travaux sur la chaussée, les mauvaises conditions climatiques, les accidents et les pannes de véhicules. Par conséquent, un réseau stochastique temporel est une représentation plus réaliste d'un réseau routier réel qu'un réseau déterministe[8]. Malgré des progrès considérables, la définition et l'identification d'un chemin optimal dans les réseaux routiers stochastiques reste un sujet controversé. En d'autres termes, il n'y a pas de définition unique d'un chemin optimal en présence d'incertitude. Une réponse possible et répandue est un chemin qui réalise le temps de déplacement minimum prévu. Le principal avantage de cette approche qu'elle permet d'utiliser les algorithmes de plus court chemin introduits pour les réseaux déterministes pour identifier le trajet avec le temps de déplacement minimum attendu dans un réseau stochastique.
Cependant, le chemin optimal peut ne pas être satisfaisant, parce que cette approche ne prend pas en compte la variabilité du temps de déplacement. Pour résoudre ce problème, certains chercheurs utilisent une distribution du temps de déplacement plutôt que la valeur moyenne, et ils obtiennent la distribution de probabilité du temps de déplacement total en utilisant différentes méthodes d'optimisation telles que la programmation dynamique et l'algorithme de Dijkstra[9]. Ces méthodes utilisent l'optimisation stochastique, et notamment la programmation dynamique stochastique pour trouver le chemin le plus court dans les réseaux à longueur d'arc probabiliste[10]. Il convient de noter que le concept de fiabilité du temps de déplacement est utilisé de façon interchangeable avec la variabilité du temps de déplacement dans la littérature de recherche sur les transports, de sorte que, en général, on peut dire que plus la variabilité du temps de déplacement est élevée, plus la fiabilité est basse et vice-versa.
Afin de rendre compte plus précisément de la fiabilité du temps de déplacement, deux définitions alternatives communes pour un chemin optimal sous incertitude ont été suggérées. Certains ont introduit le concept de chemin le plus fiable, visant à maximiser la probabilité d'arriver à temps ou plus tôt qu'un coût de déplacement donné. D'autres ont mis en avant le concept d'un chemin α-fiable sur la base duquel ils ont eu l'intention de minimiser le coût du déplacement pour assurer une probabilité d'arrivée à l'heure prédéterminée.
Complexité
Mulmulay et Shah ont donné des bornes inférieures de complexité pour le problème du plus court chemin[11].
Notes et références
- Claude Pair, « Sur des algorithmes pour des problèmes de cheminement dans les graphes finis », dans P. Rosentiehl, Théorie des graphes (journées internationales d'études) -- Theory of Graphs (internainal symposium), Dunod (Paris) et Gordon and Breach (New York),
- Jean Claude Derniame et Claude Pair, Problèmes de cheminement dans les graphes, Dunod (Paris), , 182 p.
- Alfred V. Aho, John E. Hopcroft et Jeffrey D. Ullman, The Design and Analysis of Computer Algorithms, Reading, Mass., Addison-Wesley, , 470 p. (ISBN 978-0-201-00029-0)
- Michel Gondran et Michel Minoux, Graphes, dioïdes et semi-anneaux : nouveaux modèles et algorithmes, Paris, Tec & Doc, , xvi+415 (ISBN 2-7430-0489-4, SUDOC 060235101) — Édition en anglais : (en) Michel Gondran et Michel Minoux, Graphs, Dioids and Semirings : New Models and Algorithms, Dordrecht, Springer Science & Business Media, coll. « Operations Research/Computer Science Interfaces Series » (no 41), , xix+383 (ISBN 978-0-387-75450-5, zbMATH 1201.16038, SUDOC 12874958X, lire en ligne)
- Pierre Robert et Jacques Ferland, « Généralisation de l’algorithme de Warshall », Revue française d’informatique et de recherche opérationnelle, série rouge, t. 2, no 1, , p. 71-85 (lire en ligne).
- Ittai Abraham, Amos Fiat, Andrew V. Goldberg et Renato Fonseca F. Werneck, « Highway Dimension, Shortest Paths, and Provably Efficient Algorithms », ACM-SIAM Symposium on Discrete Algorithms, , p. 782-793 (lire en ligne).
- Ittai Abraham, Daniel Delling, Andrew V. Goldberg et Renato Fonseca F. Werneck, « A Hub-Based Labeling Algorithm for Shortest Paths on Road Networks" », dans Panos M. Pardalos et Steffen Rebennack (éditeurs), Experimental Algorithms (10th International Symposium on Experimental Algorithms, Kolimpari, Chania, Crète, 5-7 mai 2011), Springer Science & Business Media, , 460 p. (ISBN 9783642206610, lire en ligne), p. 230-241.
- Mojtaba Rajabi-Bahaabadi, Afshin Shariat-Mohaymany, Mohsen Babaei et Chang Wook Ahn, « Multi-objective path finding in stochastic time-dependent road networks using non-dominated sorting genetic algorithm », Expert Systems with Applications, vol. 42, no 12, , p. 5056–5064 (DOI 10.1016/j.eswa.2015.02.046, présentation en ligne).
- Mohammad Hessam Olya, « Finding shortest path in a combined exponential – gamma probability distribution arc length », International Journal of Operational Research, vol. 21, no 1, , p. 25–37 (DOI 10.1504/IJOR.2014.064020, présentation en ligne).
- Mohammad Hessam Olya, « Applying Dijkstra’s algorithm for general shortest path problem with normal probability distribution arc length », International Journal of Operational Research, vol. 21, no 2, , p. 143–154 (DOI 10.1504/IJOR.2014.064541, présentation en ligne).
- (en) « A Lower Bound for the Shortest Path Problem », Journal of Computer and System Sciences, vol. 63, no 2, , p. 253–267 (ISSN 0022-0000, DOI 10.1006/jcss.2001.1766, lire en ligne, consulté le )
Bibliographie
- Ouvrages
- Jean Claude Derniame et Claude Pair, Problèmes de cheminement dans les graphes, Dunod (Paris), , 182 p.
- (en) Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest et Clifford Stein, Introduction to Algorithms, MIT Press et McGraw-Hill, , 2e éd. [détail de l’édition]
- Section 26.2. « The Floyd-Warshall algorithm », p. 558–565;
- Section 26.4. « A general framework for solving path problems in directed graphs », p. 570–576.
- Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest et Clifford Stein (trad. de l'anglais), Algorithmique : Cours avec 957 exercices et 158 problèmes, Dunod, [détail de l’édition]
- Chapitre 24. « Plus courts chemins à l’origine unique »
- Chapitre 25. « Plus courts chemins entre toutes paires de sommets »
- Michel Gondran et Michel Minoux, Graphes et algorithmes, Paris, Lavoisier, coll. « Études et recherches d'Électricité de France », , 4e éd. (1re éd. 1979), xxxi+784 (ISBN 978-2-7430-1035-5)
- Chapitre 2. « Le problème du plus court chemin »
- Chapitre 3. « Algèbres de chemins et dioïdes »
- (en) Alexander Schrijver, Combinatorial Optmization, Berlin/Heidelberg/New York, Springer, , 1881 p. (ISBN 3-540-44389-4, lire en ligne)
- Chapter 8. « Shortest paths : arbitrary lengths »
- Articles
- Claude Pair, « Sur des algorithmes pour des problèmes de cheminement dans les graphes finis », dans P. Rosentiehl, Théorie des graphes (journées internationales d'études) -- Theory of Graphs (internainal symposium), Dunod (Paris) et Gordon and Breach (New York),
- Ravindra K. Ahuja, Kurt Mehlhorn, James Orlin et Robert E. Tarjan, « Faster algorithms for the shortest path problem », ACM, vol. 37, no 2, , p. 213–223 (DOI 10.1145/77600.77615, lire en ligne).
- Torben Hagerup, « Improved Shortest Paths on the Word RAM », dans Ugo Montanari, José D. P. Rolim et Emo Welzl (éditeurs), Proceedings of the 27th International Colloquium on Automata, Languages and Programming, (ISBN 3-540-67715-1, lire en ligne), p. 61–72.
- Seth Pettie et Vijaya Ramachandran, « Computing shortest paths with comparisons and additions », Proceedings of the thirteenth annual ACM-SIAM symposium on Discrete algorithms, , p. 267–276 (ISBN 0-89871-513-X, lire en ligne)
- Seth Pettie, « A new approach to all-pairs shortest paths on real-weighted graphs », Theoretical Computer Science, vol. 312, no 1, , p. 47–74 (DOI 10.1016/s0304-3975(03)00402-x)
- Mikkel Thorup, « Integer priority queues with decrease key in constant time and the single source shortest paths problem », Journal of Computer and System Sciences, vol. 69, no 3, , p. 330–353 (DOI 10.1016/j.jcss.2004.04.003, lire en ligne).
- Ryan Williams, « Faster all-pairs shortest paths via circuit complexity », ACM, New York, , p. 664–673 (DOI 10.1145/2591796.2591811, MR 3238994, arXiv 1312.6680).
Articles liés
- Lexique de la théorie des graphes
- Algorithmes de plus courts chemins
- Recherche de chemin
- Algorithme de parcours en largeur
- Algorithme de Dijkstra
- Algorithme A*
- Algorithme de Bellman-Ford
- Algorithme de Floyd-Warshall
- Algorithme de Warshall
- Contractions hiérarchiques
- IEEE 802.1aq
- Réseau de flot
- Plus court chemin euclidien
- Mathématiques tropicales
- Algorithme de Johnson
- Problème de flot maximum
- Distance (théorie des graphes)










































































