Algorithme de Johnson

En informatique, l'algorithme de Johnson calcule des plus courts chemins entre toutes les paires de sommets dans un graphe orienté, aux arcs pondérés. Les poids des arcs peuvent être des nombres négatifs pourvu qu'il n'existe pas de circuits de poids négatif. Il est particulièrement efficace lorsque le graphe est creux. L'algorithme opère en utilisant d'abord l'algorithme de Bellman-Ford pour calculer une transformation du graphe de départ qui supprime tous les poids négatifs, ce qui permet l'emploi, dans un deuxième temps, de l’algorithme de Dijkstra sur le graphe transformé[1] - [2]. L'algorithme est nommé d'après Donald B. Johnson (en) qui le premier a publié cette méthode en 1977[3].

Découvreur ou inventeur	Donald B. Johnson (en)
Date de publication	1977
Problèmes liés	Algorithme, algorithme de la théorie des graphes (d), problèmes de cheminement
Structure des données	Graphe

Complexité en temps
Pire cas	$O(\|V\|^{2}\log \|V\|+\|V\|\|E\|)$

Une technique similaire de repondération est aussi utilisée dans l'algorithme de Suurballe (en) pour la recherche de deux chemins disjoints de longueur totale minimale entre deux même sommets dans un graphe pondéré positivement[4].

Description de l'algorithme

L'algorithme est composé des étapes suivantes[1] - [2] :

Ajouter un nouveau sommet $q$ au graphe, et connecter ce sommet par des arcs de poids nul à tous les autres nœuds.
Utiliser l'algorithme de Bellman-Ford en partant du nouveau sommet $q$ pour déterminer, pour chaque sommet $v$ , le poids minimum $h (v)$ d'un chemin de $q$ à $v$ . Si on détecte un cycle négatif, l'algorithme s'arrête sur un échec.
Repondérer les arcs du graphe initial en utilisant les valeurs calculées par l'algorithme de Bellman-Ford : un arc de $u$ à $v$ , dont l’ancien poids est le nombre $w(u,v)$ , a pour nouveau poids le nombre positif $w(u,v) + h(u) - h(v)$ .
Enlever le sommet $q$ et, pour tout sommet s, appliquer l'algorithme de Dijkstra depuis la source s (on peut alors déterminer des plus courts chemins de tout sommet à tout sommet dans le graphe aux nouveaux poids).

Exemple

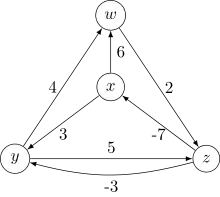Graphe initial

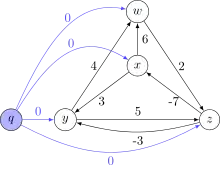Ajout d'un nouveau sommet source, noté

q

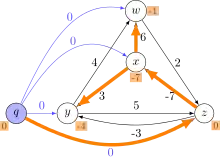Arbre couvrant des plus courts chemins produit par l'algorithme de Bellman-Ford depuis le sommet source

q

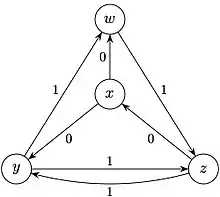Graphe repondéré positivement où on applique l'algorithme de Dijkstra en prenant chaque sommet un à un comme sommet source

Le graphe initial (à gauche dans l'illustration) possède deux arcs négatifs, mais pas de cycle négatif. On représente ensuite le graphe avec un nouveau sommet $q$ et des arcs de poids nuls vers tous les sommets du graphe initial x, y, z et w. Puis, on montre un arbre des plus courts chemins calculé par l'algorithme de Bellman-Ford avec $q$ comme sommet source. Les valeurs $h (v)$ (en orange dans le dessin) affectées à chaque nœud sont les poids des plus courts chemins de $q$ vers ce nœud. Ces valeurs sont toutes négatives ou nulles, puisque par construction $q$ a déjà un arc de poids nul vers chaque sommet et un plus court chemin ne peut être pas plus lourd que cet arc. Sur la droite est représenté le graphe repondéré. Il est formé en remplaçant chaque poids d'arc $poids(u,v)$ par $poids(u,v) + h(u) - h(v)$ . Dans ce graphe repondéré, les poids des arcs sont toujours positifs ou nuls, et un plus court chemin entre deux sommets arbitraires utilise la même séquence d'arcs qu'un plus court chemin entre ces deux mêmes sommets dans le graphe initial. L'algorithme se termine en appliquant plusieurs fois l'algorithme de Dijkstra pour chacun des quatre sommets de départ dans le graphe repondéré.

Correction de l'algorithme

La repondération est réversible

Dans le graphe repondéré, tout chemin d'un nœud $s$ à un nœud $t$ est augmenté de la même valeur $h(s)-h(t)$ .

Démonstration

En effet, soit $c=(s,p_{1},p_{2},\ldots ,p_{n},t)$ un chemin de $s$ à $t$ . Son poids dans le graphe repondéré est :

{\bigl (}poids(s,p_{1})+h(s)-h(p_{1}){\bigr )}+{\bigl (}poids(p_{1},p_{2})+h(p_{1})-h(p_{2}){\bigr )}+...+{\bigl (}poids(p_{n},t)+h(p_{n})-h(t){\bigr )}.

Chaque terme $+h(p_{i})$ est annulé par le terme $-h(p_{i})$ dans l'expression précédente entre parenthèses. C'est une somme télescopique. On obtient donc :

{\bigl (}poids(s,p_{1})+poids(p_{1},p_{2})+...+poids(p_{n},t){\bigr )}+h(s)-h(t)

L'expression entre parenthèses est le poids du chemin dans la pondération initiale. La repondération augmente donc de la même valeur $h(s)-h(t)$ chaque chemin de $s$ à $t$ .

En particulier, un chemin de $s$ à $t$ est un plus court chemin avec les poids de départ si et seulement s'il est un plus court chemin avec la nouvelle pondération. Ainsi, si on calcule des plus courts chemins dans le graphe repondéré, on obtient des plus courts chemins en inversant la transformation de repondération[1].

Le graphe repondéré est positif

D'autre part, tous les arcs du graphe repondéré sont de poids positifs.

Démonstration

Remarquons que le poids d'un plus court chemin de q à tout autre sommet u est nulle dans le graphe repondéré. En effet, un tel plus court chemin est aussi un plus court chemin dans le graphe initial où on a ajouté q. Et par définition de la repondération, le poids repondéré de chaque arc d'un tel plus court chemin est nulle. Ainsi, dans le graphe repondéré, pour tout arc (u, v), le poids du chemin q → u → v est 0 + poids(u, v). Il est supérieur à 0 car le poids d'un plus court chemin de q à v est 0. Donc l'arc (u, v) est de poids positif.

Comme les arcs sont tous de poids positifs dans le graphe repondéré, les exécutions de l'algorithme de Dijkstra sont correctes.

Pseudo-code

Entrée : G un graphe pondéré sans cycle de poids négatif
Sortie : les distances entre toutes paires de sommets
Johnson(G)
          G1 := G où on a ajouté un sommet q et des arcs entre q et tout sommet de G
          h[.] := Bellman-Ford(G1, q)
          G2 := G où pour chaque arc (s, t), le poids de (s, t) est poids(s, t) + h(s) - h(t) où poids(s, t) est le poids de (s, t) dans G
          pour tout sommet s de G
                    d[s, .] := Dijkstra(G, s)
          pour tout s, t sommets de G
                    d[s, t] := d[s, t] - (  h(s) - h(t) )
          retourner d

Analyse de complexité

La complexité en temps de cet algorithme est, en utilisant un tas de Fibonacci pour l’implémentation de l'algorithme de Dijkstra, en $O(|V|^{2}\log |V|+|V||E|)$ . L'algorithme prend en effet un temps $O(|V||E|)$ pour la phase composée de l'algorithme de Bellman-Ford, et $O(|V|\log |V|)$ pour chacun des $| V |$ appels de l'algorithme de Dijkstra. Ainsi, lorsque le graphe est creux, le temps total peut être inférieur à celui de l'algorithme de Floyd-Warshall qui résout le même problème en temps $O(|V|^{3})$ [1].

Notes et références

Section 25.3, « Algorithme de Johnson pour les graphes peu denses », p. 616-620 dans : Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest et Clifford Stein, Introduction à l'algorithmique, Dunod, 2002 [détail de l’édition]
Paul E. Black, « Johnson's Algorithm », dans Dictionary of Algorithms and Data Structures, National Institute of Standards and Technology, 2004 (lire en ligne).
Donald B. Johnson, « Efficient algorithms for shortest paths in sparse networks », Journal of the ACM, vol. 24, n^o 1,‎ 1977, p. 1–13 (DOI 10.1145/321992.321993).
J. W. Suurballe, « Disjoint paths in a network », Networks, vol. 14, n^o 2,‎ 1974, p. 125–145 (DOI 10.1002/net.3230040204).

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Johnson's algorithm » (voir la liste des auteurs).

Liens externes

Boost: All Pairs Shortest Paths. Un programme en C++

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.