Pavage d'une surface
Un pavage d'une surface est un ensemble de portions de la surface considérée, dont l'union est la surface tout entière, sans recouvrement.
On s'intéresse particulièrement au pavage par des « polygones » (sur une surface non plane, un polygone a pour côtés des segments d'orthodromie, c'est-à-dire des arcs constituant le plus court chemin d'un sommet du polygone au suivant), et notamment par des polygones réguliers.
Les pavages les plus étudiés sont ceux du plan, de la sphère, de l'hyperboloïde et du tore.
Coloriage
Une question apparemment anodine concerne le nombre de couleurs nécessaire au coloriage des différentes portions de surface (ou régions), de telle sorte que deux régions limitrophes (c'est-à-dire, ayant une frontière commune) ne reçoivent pas la même couleur. On sait depuis longtemps qu'en pratique il suffit de quatre couleurs sur le plan ou sur la sphère[alpha 1], mais c'est une conjecture énoncée en 1852 qui n'a été démontrée qu'en 1976 (théorème des quatre couleurs).
Sur une surface fermée[alpha 2] non homéomorphe à la sphère, Heawood a démontré en 1890 qu'il suffit de p couleurs, avec :
où E désigne la fonction partie entière et χ la caractéristique d'Euler de la surface.
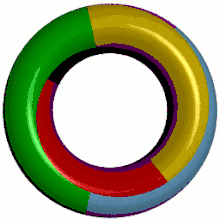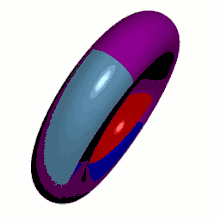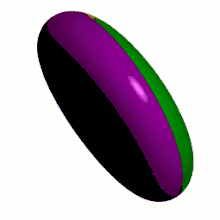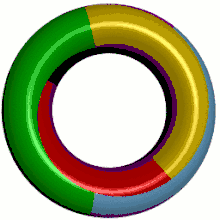
- sphère et plan : χ = 2 donc p = 4 (mais le théorème de Heawood ne s'y applique pas) ;
- tore et bouteille de Klein : χ = 0 donc p = 7 ;
- double tore (en) : χ = −2 donc p = 8 ;
- triple tore (en) : χ = −4 donc p = 9.
Sur la sphère comme sur le tore on trouve facilement des exemples de pavages où p couleurs sont nécessaires. Heawood conjecturait que c'est vrai pour toutes les surfaces, mais Philip Franklin a montré en 1934 que 6 couleurs suffisent toujours pour la bouteille de Klein (alors que p = 7), et aussi qu'elles peuvent être nécessaires (graphe de Franklin).
En 1968, Ringel et Youngs ont finalement démontré que la conjecture de Heawood est vraie pour toute surface fermée autre que la bouteille de Klein, c'est-à-dire qu'on peut tracer sur la surface une carte nécessitant p couleurs.
Pavage par des polygones réguliers
Rappelons que sur une surface non plane la notion de polygone se généralise à celle de figures formées par un certain nombre de points (les sommets) reliés de proche en proche par des segments d'orthodromie (qui réalisent le plus court chemin, sur la surface, d'un sommet à l'autre), les côtés. Quand on s'intéresse aux pavages on ne considère que des polygones convexes.
Pavages uniformes
Un pavage uniforme (en) est un pavage par des polygones réguliers et isogonal, c'est-à-dire que tous les sommets sont identiques (ils sont entourés des mêmes types de face et dans le même ordre, et ces faces forment les mêmes angles).
Pavages réguliers
Un pavage régulier est un pavage par des polygones réguliers tous identiques.
On peut paver le plan avec des triangles (équilatéraux), des carrés ou des hexagones (réguliers).
On peut paver la sphère par 4, 8 ou 20 triangles (équilatéraux), 6 carrés ou 12 pentagones (réguliers)[alpha 3]. On peut aussi la paver par un nombre quelconque de dièdres sphériques (en) n-gonaux mais il s'agit de pavages dégénérés (angles aux sommets de 180°).
Pavages semi-réguliers
Un pavage semi-régulier est un pavage par au moins deux types de polygones réguliers, de telle façon qu'un sommet soit toujours entouré des mêmes polygones, dans le même ordre.
Dans le cas du plan, il existe huit pavages semi-réguliers, dont un, le pavage hexagonal adouci, est chiral (il en existe deux variantes non superposables, symétriques l'une de l'autre par une symétrie axiale).
Notes et références
Notes
- La question du coloriage est la même pour la sphère que pour le plan. On peut s'en rendre compte en retirant de la sphère un point intérieur à l'une des régions, et en effectuant depuis ce point une projection stéréographique.
- Une surface est fermée si elle est compacte, connexe et sans bord.
- On obtient ces pavages en projetant depuis le centre de la sphère n'importe quel polyèdre régulier de même centre.




