Accueil🇫🇷Chercher

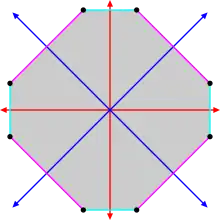
Figure isogonale

En géométrie, un polytope (un polygone ou un polyèdre, par exemple) est dit isogonal si tous ses sommets sont identiques. Autrement dit, chaque sommet est entouré du même type de face dans le même ordre et avec les mêmes angles entre les faces correspondantes.

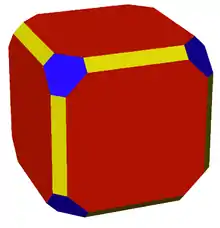
Exemple : Un cuboctaèdre tronqué isogonal, construit à partir d'un cube aux arêtes chanfreinées et aux sommets tronqués.

Plus précisément : le groupe de symétrie du polytope agit transitivement sur l'ensemble des sommets.

Polygone isogonal
Un octogone isogonal convexe et ses quatre axes de symétrie[1].

Tous les polygones réguliers, qu'ils soient convexes ou étoilés, sont isogonaux.

Les autres polygones isogonaux sont les polygones équiangles à 2n côtés (n = 2, 3…) dont la longueur prend alternativement deux valeurs différentes, comme le rectangle. Ils présentent une symétrie diédrale Dn avec n axes de symétrie reliant les milieux des côtés opposés.

Les duaux des polygones isogonaux sont les polygones isotoxaux.

Polyèdre isogonal

Les polyèdres isogonaux peuvent être classés en :

  • Régulier s'il est également isoédrique et isotoxal ; ceci implique que chaque face soit un même polygone régulier.
  • Quasi-régulier s'il est également isotoxal mais non nécessairement isoédral.
  • Noble (en) s'il est également isoédral mais non nécessairement isotoxal.
  • Semi-régulier si chaque face est un polygone régulier mais que le polyèdre n'est ni isoèdral ni isotoxal.
  • Uniforme si chaque face est un polygone régulier, c'est-à-dire que le polyèdre est régulier, quasi-régulier ou semi-régulier.

Un polyèdre isogonal est un cas particulier de figure de sommet. Si les faces sont régulières (et que donc le polyèdre est uniforme) il peut être représenté par une configuration de sommets indiquant la suite des faces autour de chaque sommet.

Polytopes isogonaux et tessellations

Cette définition peut être étendue aux polytopes et aux tessellations. Plus généralement, les polytopes uniformes (en) sont isogonaux, par exemple, les 4-polytopes uniformes et les nids d'abeille uniformes convexes (en).

Le dual d'un polytope isogonal est isoédral.

Figures k-isogonales

Un polytope est dit k-isogonal si ses sommets forment des classes k-transitives.


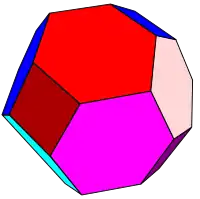Ce dodécaèdre rhombique tronqué est 2-isogonal car il contient 2 classes de transitivité de sommets. Ce polyèdre est formé de carrés et d'hexagones aplatis.
Ce pavage semi-régulier est également2-isogonal. Il est constitué de triangles équilatéraux, de carrés et d'hexagones réguliers.

Notes et références
(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Isogonal figure » (voir la liste des auteurs).
  1. La catégorie « Polygones tronqués » de Commons contient beaucoup d'autres exemples de polygones isogonaux, convexes ou croisés.
  • (en) Peter R. Cromwell, Polyhedra, Cambridge University Press, 1999 (ISBN 978-0-52166405-9) (p. 369 : transitivity)
  • (en) Branko Grünbaum et Geoffrey Shephard, Tilings and Patterns, New York, Freeman, , 700 p. (ISBN 978-0-7167-1193-3, LCCN 86002007) (p. 33 : k-isogonal tiling, p. 65 : k-uniform tilings)

Liens externes
Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.