Figure de sommet
En géométrie, une figure de sommet d'un sommet donné d'un polytope est, de façon intuitive, l'ensemble des points directement reliés à ce sommet par une arête. Ceci s’applique également aux pavages infinis, ou pavages remplissant l’espace avec des cellules polytopiques.
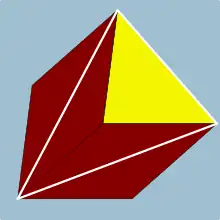
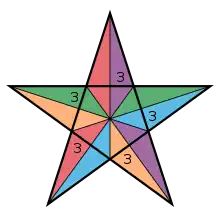
De façon plus précise, une figure de sommet pour un n-polytope est un (n-1)-polytope. Ainsi, une figure de sommet pour un polyèdre est une figure polygonale, et la figure de sommet pour un polychore est une figure polyèdrique. Le (n-1)-polytope, figure de sommet correspondant à un sommet A donné du n-polytope, est défini comme suit :
- Chaque sommet de la figure de sommet correspond à une arête du polytope original, issu de A.
- Chaque arête de la figure de sommet correspond à une face du polytope original, et relie deux sommets consécutifs de la figure de sommet qui correspondent dans le polytope initial à deux arêtes de cette même face.
- Chaque face de la figure de sommet correspond à une 3-cellule du n-polytope original (pour n>3), ses arêtes correspondant dans le polytope initial à des faces appartenant à cette même 3-cellule.
- … et ainsi de suite pour les éléments d’ordre plus élevés dans les polytopes d’ordres plus élevés.
Les figures de sommet sont les plus utiles pour les polytopes uniformes (en) car une figure de sommet peut impliquer le polytope entier.
Pour les polyèdres, la figure de sommet peut être représentée par une notation de configuration de sommet, en listant les faces dans une suite autour du sommet. Par exemple 3.4.4.4 est un sommet avec un triangle et trois carrés, et il représente le petit rhombicuboctaèdre.
Si le polytope est de sommet uniforme, la figure de sommet existera dans une surface hyperplane du n-espace. En général, les figures de sommet n’ont pas besoin d’être planaires.
Comme les polyèdres non convexes, les figures de sommet peuvent aussi être non convexes. Les polytopes uniformes peuvent avoir des faces en polygones étoilés et des figures de sommet par exemple.
Polytopes réguliers
Si un polytope est régulier, il peut être représenté par un symbole de Schläfli et, la cellule et la figure de sommet peuvent tous deux être extraits trivialement de cette notation.
En général, un polytope régulier avec un symbole de Schläfli {a,b,c,...,y,z} possède des cellules {a,b,c,...,y}, et des figures de sommet {b,c,...,y,z}.
- Pour un polyèdre régulier {p, q}, la figure de sommet est {q}, un q-gone.
- Exemple, la figure de sommet pour un cube {4,3} est le triangle {3}.
- Pour un polychore régulier ou un pavage remplissant l’espace {p,q,r}, la figure de sommet est {q,r}.
- Exemple, la figure de sommet pour un hypercube {4,3,3} est un tétraèdre régulier {3,3}.
- La figure de sommet pour un nid d’abeille cubique (en) {4,3,4} est l’octaèdre régulier {3,4}.
Puisque le polytope dual d’un polytope régulier est aussi régulier et est représenté par le symbole de Schläfli dont les indices sont inversés, il est facile de voir que la figure de sommet du dual est la cellule du polytope dual.
Un exemple de figure de sommet d'un nid d'abeille
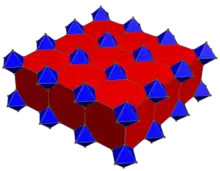
La figure de sommet d’un nid d’abeille cubique tronqué (en) est une pyramide carrée non uniforme. Un octaèdre et quatre cube tronqués se rencontrent à chaque sommet pour former un pavage remplissant l’espace.
| Figure de sommet : Une pyramide carrée non uniforme | 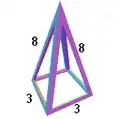 |
| Créée comme une base carrée à partir d’un octaèdre |  |
| Et quatre côtés en triangles isocèles à partir de cubes tronqués | 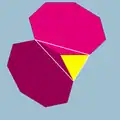 |
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Vertex figure » (voir la liste des auteurs).