Mémoire sur la diffraction de la lumière (Fresnel, 1818)

La théorie corpusculaire de la lumière, adoptée par Isaac Newton et par presque tous les physiciens contemporains de Fresnel, expliquait aisément la propagation rectiligne de la lumière. La théorie ondulatoire, développée par Christian Huygens dans son Traité de la Lumière, explique la propagation en ligne droite en assumant que chaque point d'un front d'onde est la source d'ondelettes secondaires dont les enveloppes forment les fronts d'onde successifs suivant. Ce que Newton réfutait car si la lumière était formée d'ondes, alors, comme les ondes sonores ou les ondes à la surface de l'eau, elle devrait se courber au voisinage d'un obstacle, diffuser dans toutes les directions, y compris dans l'ombre de l'obstacle[5]

Avec sa théorie, Huygens avait pu expliquer élégamment la loi de la réflexion et la loi de la réfraction (la loi de Snell-Descartes) en posant que les rayons lumineux suivent les trajets de moindre durée, selon le principe de Fermat. Newton avait pu aussi expliquer ces lois avec sa théorie, mais à condition de considérer que la lumière se déplaçait plus vite dans les milieux plus denses, ce qui est faux.

Newton avait envisagé que la lumière puisse être formée d'ondulations périodiques pour expliquer les irisations apparaissant sur les lames minces comme les bulles de savon ou les anneaux colorés (Anneaux de Newton). Il avait même émis l'idée que la lumière rouge devait avoir des longueurs ondes plus longues que celles de la lumière violette. Il publia ces hypothèses en 1672 mais elles n'intéressèrent pas les savants de l'époque, comme Robert Hooke, pourtant partisans de la théorie ondulatoire[6]. Newton est donc revenu à la théorie corpusculaire en affectant les corpuscules lumineux de capacités (fits) de transmission aisée ou de réflexion aisée[7] - [8], le passage d'une capacité à l'autre dépendant de la couleur et du milieu[9] et, bizarrement, de l'angle de réflexion ou de réfraction[10]. Plus bizarrement encore, cette théorie exige que les lames minces ne réfléchissent qu'à leur surface interne alors qu'il est manifeste que les lames minces réfléchissent aussi à leur surface externe[11]. Ce n'est qu'en 1801, que Thomas Young, citant l'hypothèse fugace de Newton, expliqua les couleurs des films minces en notant que si l'on admet que les rayons réfléchis par la face supérieure se combinent avec ceux qui sont réfléchis par la face inférieure, ils devaient se renforcer ou s'annuler en fonction de la longueur d'onde et de l'épaisseur de la lame. Il nomma le phénomène interférence[12].

Thomas Young (1773–1829)

Ni Newton, ni Huygens, n'ont donné une explication satisfaisante de la diffraction, le caractère flou de la limite des ombres portées. Selon la théorie corpusculaire, la limite de l'ombre devrait être nette puisque la lumière se propage en ligne droite. Pour rendre compte du phénomène, Newton a supposé que les rayons lumineux sont infléchis, c'est-à-dire courbés, par une force attractive ou répulsive exercée par le bord des obstacles. Mais cette explication était purement qualitative[13]. Dans sa conférence de 1801, Young reprend le modèle de Huygens et explique qu'au bord de l'obstacle les ondelettes secondaires peuvent rayonner dans toutes les directions, y compris dans l'ombre. Les fanges d'interférences observées à l'extérieur de l'ombre devaient résulter de la combinaison de rayons infléchis et de rayons réfléchis par le bord de l'obstacle[14].

Dans sa conférence de 1803, Young montra que les franges observées à l'intérieur de l'ombre d'un objet étroit provenait de l'interférence de rayons issus de chaque côté de l'objet[15]. Mais les observations de Young n'ont suscité aucun intérêt de la part de ses collègues qui jugeaient arrogant d'oser contester la théorie de Newton[16].

Un regain d'intérêt pour l'optique est né quand Étienne Louis Malus publia en 1809 ses observations sur la polarisation de la lumière par réflexion. Bien qu'il ait repris les travaux de Huygens sur la biréfringence, il chercha, sur les conseils de Pierre-Simon de Laplace, une explication du phénomène par la théorie corpusculaire de Newton en invoquant le principe de moindre action de Maupertuis. Mais Young fit remarquer que l'on pouvait donner une explication équivalente avec la théorie ondulatoire en invoquant le principe de Fermat[17]. A la suite de ces travaux, François Arago et Jean-Baptiste Biot entreprirent des études sur la biréfringence de lames et de cristaux de calcite et de quartz. C'est une communication de Biot qui attira l'attention de Fresnel en 1814.

Vers 1812, Fresnel, qui était polytechnicien et ingénieur des Ponts et Chaussées, fut envoyé à Nyons, dans la Drôme, sur le chantier de la route impériale qui devait relier l'Italie à l'Espagne[18]. C'est à Nyons qu'il manifeste son intérêt pour l'optique. Le 15 mai 1814, il écrit en post-scriptum à une lettre à son frère Léonor :

« Je voudrais bien avoir aussi des mémoires qui me missent au fait des découvertes des physiciens français sur la polarisation de la lumière. J'ai vu dans Le Moniteur, il y a quelques mois, que Biot avait lu à l'Institut un mémoire fort intéressant sur le polarisation de la lumière[19]. J'ai beau me casser la tête, je ne devine pas ce que c'est »[20].

Portrait de François Arago par Charles de Steuben, 1832.

En mars 1815, Napoléon débarque de l'île d'Elbe. Fresnel, qui est royaliste, se range aux côtés de la résistance royale à Lapalud dans le Vaucluse mais il n'est pas enrôlé à cause de son apparence chétive. « Fresnel rentra à Nyons, presque mourant... La populace lui fit subir mille outrages » dit Arago[21]. Il est arrêté à Valence le 8 mai 1815. Il est relâché mais est destitué pendant les Cent-jours tout en ayant l'autorisation de se rendre chez sa mère à Mathieu dans le Calvados. « Fresnel obtint la permission de passer par Paris. Il put renouer connaissance avec d'anciens condisciples et se préparer ainsi aux recherches scientifiques dont il comptait s'occuper dans la retraite où ses jeunes années s'étaient écoulées ». Le 12 juillet, alors que Fresnel est sur le départ, Arago lui laisse une note dans laquelle il attire son attention sur la diffraction de la lumière :

« Je ne connais pas d'ouvrage qui renferme la totalité des expériences que les physiciens ont faites sur la diffraction de la lumière. Monsieur Fresnel ne pourra se mettre au courant de cette partie de l'optique qu'en lisant l'ouvrage de Grimaldi, celui de Newton, le traité anglais de Jordan et les Mémoires de Brougham et de Young, qui font partie de la collection des Transactions philosophiques[22]. »

Fresnel n'a pas accès à ces publications en dehors de Paris et ne parle pas anglais[23]. Malgré ces difficultés, arrivé à Mathieu, il entreprend des expériences sur la diffraction et les interférences de la lumière[24] - [25]. Trois mois plus tard, il envoie, le 15 octobre, un manuscrit intitulé Mémoire sur la diffraction de la lumière à Delambre, secrétaire perpétuel de l'Institut, par l'intermédiaire de son oncle. Le 20 novembre, il envoie un nouveau manuscrit pour décrire les expériences complémentaires qu'il a faites sur la diffraction. Il annonce aussi, qu'ayant été réintégré dans le corps des Ponts et Chaussées, il doit se rendre à Rennes où il est affecté.

Portrait d'Augustin Fresnel.

Les travaux de Fresnel à Mathieu ont été examinés par Arago qui lui a fait remarquer qu'il avait en grande partie reproduit les travaux de Young mais que certaines de ses observations étaient nouvelles. Comme Fresnel avait fait ses expériences avec la lumière du soleil, Arago lui a conseillé de venir les refaire à Paris en lumière monochromatique pour obtenir des mesures plus précises et incontestables. Ce que Fresnel pu faire au début de 1816. Il explique de façon satisfaisante la formation des franges dans l'ombre d'un objet étroit (un fil) et de façon approximative les franges à l'extérieur de l'ombre.

D'après Emile Verdet « Ce qui appartient en propre à Fresnel et dont on n'aperçoit aucune trace chez ses devanciers, c'est l'idée féconde d'expliquer les lois de la réflexion et de la réfraction par le principe des interférences[26]. » Fresnel a aussi remarqué que « les rayons qui ont été obscurcis par la discordances de leurs vibrations redeviennent lumineux ensuite dans la partie du trajet où les ondulations sont d'accord, et qu'ainsi ils peuvent reprendre leur éclat après l'avoir perdu momentanément[27]. » Le résultat de l'interférence des ondes est transitoire et localisé dans l'espace et le temps. Les ondes poursuivent leur chemin, en se superposant, si on ne les arrête pas sur un écran d'observation. Ce qui constitue une expression du Principe de superposition.

Finalement, une version corrigée et enrichie est présentée à l'Académie par Arago, le 25 mars 1816[28]. Intitulé Mémoire sur la diffraction de la lumière, où l'on examine particulièrement le phénomène des franges colorées que présentent les ombres des corps éclairés par un point lumineux, il est publié dans le numéro de mars 1816 (paru en mai) des Annales de Chimie et de Physique. Il est reproduit dans les Œuvres complètes sous le titre Deuxième Mémoire[29].

Dans ce supplément envoyé trois semaines après le premier Mémoire, Fresnel présente ses expériences et ses interprétations des réseaux optiques, des anneaux de Newton, des franges externes à l'ombre portée d'un corps opaque, du miroir double et de la figure de diffraction d'une fente lumineuse. Le Supplément au premier Mémoire sur la diffraction de la lumière est présenté à l'académie le 15 juillet 1816 par Arago[30]. « On trouve pour la première fois exposées dans ce Mémoire les causes mécaniques vraies de la diffraction, mais l'auteur n'était pas encore parvenu, à cette époque, à résoudre toutes les difficultés que présentait la théorie dans son application aux phénomènes ». (Note d'Émile Verdet[31])

L'Académie des sciences a annoncé le 17 mars 1817 que le thème du prochain Grand Prix de Physique de l'Académie, qui serait attribué en 1819, serait la diffraction de la lumière. Les manuscrits devaient être déposés avant le 1er août 1818 pour permettre au jury d'examiner les travaux et, éventuellement, de les vérifier expérimentalement. Fresnel était occupé par ses recherches sur la polarisation de la lumière, qu'il menait en marge de ses fonctions d'ingénieur des Ponts et Chaussées. Arago et Ampère l'ont incité à concourir et donc à reprendre ses travaux sur la diffraction.

Fresnel produisit deux articles préparatoires dans lesquels il décrivait les bases mathématiques de la théorie des ondes lumineuses. Le 15 janvier 1818, dans une note additionnelle à un article sur la polarisation[32], il établissait l'équation des ondes lumineuses sous forme de fonctions sinusoïdales et montrait que l'on peut exprimer la composition de deux ondes sous une forme analogue à la composition de deux forces (le concept de vecteur n'existait pas encore). Dans une note sous pli cacheté déposée le 20 avril 1818, Fresnel esquissait une théorie élémentaire de la diffraction[33] en reformulant le principe de Huygens en combinaison avec le Principe de superposition.

C'est en reprenant l'ensemble de ses travaux précédents qu'il rédige le second Mémoire sur la diffraction de la lumière qu'il a soumis à l'Académie le 29 juillet 1818 de façon anonyme avec l'épigraphe Natura simplex et fecunda (La nature est simple et fertile), qui devait permettre de l'identifier.

Siméon Denis Poisson (1781–1840)

Le jury du concours était composé de Laplace, Biot et Poisson (tous tenant de la théorie corpusculaire newtonienne), Gay-Lussac (neutre), et Arago qui, à la fin, écrit le rapport du jury[34]. Bien que les soumissions soient en principe anonymes, le rapport de Fresnel était identifiable par son contenu[35]. De toute façon, il n'y a eu qu'une seule autre soumission dont ni le manuscrit ni l'auteur n'ont laissé de trace. L'existence de cette autre soumission est mentionnée seulement dans le dernier paragraphe du rapport du jury[36] et indique que l'auteur ignore les travaux précédents de Young et de Fresnel, utilise des méthodes d'observation insuffisamment précises, néglige certaines choses et fait des erreurs manifestes. On peut en déduire que le jury avait deux options : donner le prix à Fresnel ou ne pas l'attribuer.

Fig.1-Ombre portée par un disque de 5.8 mm de diamètre sur un écran à 183 cm, par la lumière du soleil passant par un petit trou placé à 153 cm du disque. Les faibles couleurs des franges montrent la dépendance à la longueur d'onde diagramme de diffraction. Au centre, on peut distinguer la tache de Fresnel.

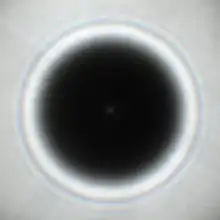
L'examen du jury dura jusqu'à l'année suivante. C'est alors que Poisson, exploitant un cas où la théorie de Fresnel donnait des intégrales faciles, trouva que la théorie prédisait l'existence d'un point lumineux au centre de l'ombre portée d'un petit disque éclairé par une source ponctuelle. Ceci semblait être une preuve par l'absurde que la théorie de Fresnel était fausse. Arago, intrigué par la démonstration de Poisson, réalisa l'expérience avec un disque opaque de 2 mm de diamètre et observa que, effectivement, une tache claire apparaissait au centre de l'ombre[37] - [38].

Le jury unanime accorda le Grand Prix au mémoire portant la sentence Natura simplex et fecunda le 15 mars 1819[39]. Après l'annonce, le président de séance ouvrit une enveloppe cachetée accompagnant le mémoire et révéla que l'auteur était Augustin Fresnel[40]. Le résultat fut officiellement annoncé à la séance publique de l'Académie, le 22 mars.

La vérification par Arago de la prédiction contre-intuitive de Poisson est passé dans l'histoire comme étant à l'origine de la décision d'attribution du prix[41].

Fresnel présente l'état des conceptions sur la lumière, leurs atouts et leurs défauts vis-à-vis des phénomènes observés.

« Quelques considérations générales sur les deux systèmes qui ont partagé jusqu'à présent les savans relativement à la nature de la lumière. Newton a supposé que les molécules lumineuses, lancées par des corps qui nous éclairent, arrivent directement jusqu'à nos yeux où elles produisent par leur choc, la sensation de la vision. Descartes, Hook, Huygens, Euler, ont pensé que la lumière résultait des vibrations d'un fluide universel extrêmement subtil, agité par les mouvements rapides des particules des corps lumineux, de la même façon que l'air est ébranlé par les vibrations des corps sonores; en sorte que, dans ce système, ce ne sont pas les corps lumineux qui parviennent à l'organe de la vue, mais seulement le mouvement qui leur a été imprimé[42]. »

« Dans le système de l'émission, il semble que rien ne devrait être plus simple que le phénomène des ombres portées, surtout quand l'objet éclairant est réduit à un point lumineux, et, cependant, rien n'est plus compliqué[43]. »

Les contours de l'ombre ne sont pas nets. En lumière blanche, des franges colorées apparaissent à la limite de l'ombre sur la partie éclairée. En lumière monochromatique, c'est une alternance de bandes sombres et brillantes qui se manifeste sur le côté éclairé. Fresnel définit comme franges extérieures celles qui apparaissent côté lumière, et franges intérieures, celles qui apparaissent dans l'ombre géométrique. il appelle ombre géométrique l'ombre que le corps opaque projetterait si la lumière se déplaçait strictement en ligne droite, sans inflexion[44].

Fresnel indique qu'il utilise une loupe pour examiner la formation des franges, au lieu d'un écran, ce qui lui permet à la fois plus de liberté d'observation à différentes positions dans l'espace et une plus grande précision dans ses mesures. Il mesure la position des franges extérieures produites par le bord droit d'un corps opaque. Il constate qu'une loi répondant aux hypothèses de Newton donne des résultats en désaccord avec l'expérience alors qu'une loi déduite de la théorie ondulatoire donne des résultats proches des observations.

« On voit donc que l'hypothèse des condensations et des dilatations produites par l'action des corps sur les rayons lumineux est insuffisante pour expliquer les phénomènes de diffraction. A l'aide du principe des interférences, au contraire, on peut concevoir non seulement les variations de largeur que les franges extérieures éprouvent lorsqu'on rapproche ou qu'on éloigne l'écran du point lumineux, mais encore le mode curviligne de leurs bandes obscures et brillantes[45]. »

Pour introduire la théorie des interférences, il cite Grimaldi qui, le premier, a reconnu l'action que les rayons lumineux exercent les uns sur les autres. Il cite l'expérience des deux fentes du célèbre professeur Thomas Young. Il évoque aussi ses propres expériences des interférences

• avec deux miroirs formant un angle très ouvert et donnant deux images d'une même source lumineuse.
• à l'intérieur de l'ombre d'un corps étroit
• au bord rectiligne de l'ombre d'un écran opaque

"Les franges que l'on observe dans l'intérieur de l'ombre d'un corps étroit, ou celles qu'on obtient avec deux miroirs, résultant évidemment de l'influence mutuelle des rayons lumineux, l'analogie indique qu'il doit en être de même pour les franges extérieures qui bordent l'ombre des corps éclairés par un point lumineux. La première hypothèse qui se présente à la pensée, c'est qu'elle sont produites par la rencontre des rayons directs et des rayons réfléchis sur les bords du corps opaque, tandis que les franges intérieures résultent de l'action réciproque des rayons infléchis dans l'ombre, des deux côtés du corps opaque, ces rayons infléchis partant également de sa surface, ou de points infiniment voisins[46].

La réflexion des rayons sur le bord du corps opaque est une hypothèse empruntée à Newton et à Young, qui se révèlera fausse. Il expose cependant le dispositif et compare le résultat des calculs aux mesures effectuées. En posant a=SA, la distance de la source au corps opaque et b=AP, la distance du corps opaque au point d'observation, x=EP, la distance du point P au bord de l'ombre géométrique E, la différence de chemin d entre un rayon direct SP et un rayon SAP réfléchi par le bord de l'obstacle sera :

${\displaystyle d=SA+AP-SP={\frac {a\,x^{2}}{2b(a+b)}}}$

La distance x du point P au bord de l'ombre sera :

${\displaystyle x={\sqrt {\frac {2db(a+b)}{a}}}}$

Si λ désigne la longueur d'onde de deux ondes parcourant des chemins différents, elle s'additionneront lorsque ${\displaystyle d=k\lambda }$, k entier positif ou nul, et elles se détruiront quand ${\displaystyle d=(2k+1)\lambda /2}$. Par conséquent, la frange obscure du premier ordre devrait être observée à une distance du bord de l'ombre égale à :

${\displaystyle x={\sqrt {\frac {b\lambda (a+b)}{a}}}}$

« Mais il résulte, au contraire, de l'observation que c'est à peu près l'endroit le plus brillant de la première frange[47]. » Pour faire mieux correspondre le résultat de la formule avec les données expérimentales, il faut considérer que la réflexion introduit une augmentation du chemin d'une demi ondulation. Si on intègre cette hypothèse, les résultats du calcul se rapprochent des mesures sans être complètement satisfaisants et la position des franges obscures sera donnée approximativement par la formule :

${\displaystyle x={\sqrt {\frac {2kb\lambda (a+b)}{a}}}}$

Cette formule entraine deux conséquences. Premièrement, la répartition des franges dépend de a, la distance de la source lumineuse au corps opaque. Deuxièmement, « La conséquence la plus remarquable de cette formule, c'est que, a restant constant, la distance de la bande obscure ou brillante que l'on considère au bord de l'ombre géométrique, n'est pas proportionnelle à b; en sorte que cette bande ne parcourt point une ligne droite, mais une hyperbole dont la courbure doit être sensible. C'est aussi ce que l'expérience confirme[48]. »

Fig.2-Parcours des rayons lumineux au voisinage d'un obstacle étroit

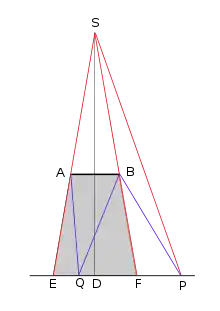
« Je passe maintenant aux franges intérieures formées dans l'ombre par le concours de deux faisceaux lumineux infléchis en A et B. Soit un point Q quelconque pris à l'intérieur de l'ombre : l'intensité de la lumière en ce point dépend du degré d'accord ou de discordance entre les rayons AQ et BQ. Je représente par x la distance QD du point Q au milieu de l'ombre et par d la différence entre les chemins parcourus[49]. Je trouve : »

${\displaystyle d={\sqrt {b^{2}+({\frac {c}{2}}+x)^{2}}}-{\sqrt {b^{2}+({\frac {c}{2}}-x)^{2}}}}$

En développant les expressions et en négligeant les puissances supérieures de x qui est très petit devant a ou b, on obtient :

${\displaystyle d={\frac {cx}{b}}\,\,\,\,\Longrightarrow \,\,\,\,x={\frac {bd}{c}}}$

Les franges obscures apparaîtront pour ${\displaystyle d=(2k+1)\lambda /2}$, soit aux positions :

${\displaystyle x={\frac {(2k+1)b\lambda }{2c}}}$

Et elles seront équidistantes les unes des autres de ${\displaystyle b\lambda /c}$. Cet espacement apparaît indépendant de la distance de la source au corps opaque, ce qui est exact au centre de l'ombre. Lorsqu'on s'approche des bords de l'ombre, l'espacement tend à croître.

Malgré l'apparente concordance des résultats expérimentaux avec les calculs, Fresnel constate expérimentalement que « on ne peut pas attribuer les phénomènes de la diffraction aux seuls rayons qui touchent les bords des corps, et qu'il faut admettre qu'une infinité d'autres rayons séparés de ces corps par des intervalles sensibles se trouvent néanmoins écartés de leur première direction, et concourent aussi à la formation des franges[50]. »

De plus, il multiplie les expériences pour démontrer que ni la forme des bords de l'objet occultant, arrondi ou tranchant, poli ou mat, ni la matière ni la masse de l'objet, n'ont d'influence sur le trajet des rayons lumineux. Il en déduit que « les phénomènes de la diffraction sont inexplicables dans le système de l'émission [de Newton][51]. »

« C'est M. Thomas Young qui le premier a introduit le principe des interférences en optique, où il en a fait beaucoup d'applications ingénieuses. Mais, dans les problèmes d'optique qu'il a résolu de cette manière, il n'a considéré, je crois, que les cas extrêmes d'accord ou de discordance complète entre deux systèmes d'ondes, sans calculer l'intensité de la lumière pour les cas intermédiaires et pour un nombre quelconque de système d'ondes, comme je me propose de le faire ici[52]. » Il faut rappeler ici ce que disait Laplace : « Young n'a jamais bien compris la différence entre un aperçu et une démonstration[53]. » Fresnel s'attaque donc à la démonstration en mettant en équation les ondes lumineuses.

En 1818, il traite encore les ondes lumineuses comme des ondes de pression, longitudinales. Cependant, en 1819, au moment de l'impression du Mémoire, il s'est convaincu « que les vibrations lumineuses s'exécutent perpendiculairement aux rayons ou parallèlement à la surface d'onde[54] » et qu'elles sont donc transversales. Il remarque que cela n'a pas d'incidence sur la validité de son raisonnement. Il suppose que les vibrations des particules éclairantes suivent les mêmes lois que les petites oscillations d'un pendule et qu'on peut exprimer leur mouvement sous la forme[55] :

${\displaystyle u=a\,\sin 2\pi (t-{\frac {x}{\lambda }})\,}$

Fresnel prend en compte la longueur d'ondulation, c'est-à-dire la longueur d'onde, mais semble ignorer le terme de fréquence (${\displaystyle \nu }$).Tout en restant au plus proche de son expression, nous posons :

${\displaystyle u=a\,\sin 2\pi ({\frac {x}{\lambda }}-\nu t)\,}$

Dans le cas de deux ondes concourantes, Fresnel pose ensuite que « l'onde résultant du concours des deux autres, quelles que soient leur positions relatives, répond exactement, pour son intensité et pour sa situation, à la résultante de deux forces égales aux intensités des deux faisceaux lumineux, et faisant entre elles un angle qui soit à la circonférence entière comme l'intervalle qui sépare les deux systèmes d'ondes est à la longueur d'une ondulation[56] ». Ce qui veut dire qu'il propose de représenter les deux faisceaux lumineux par des vecteurs ayant chacun son amplitude propre et qui forment entre eux un angle égal à ${\displaystyle \alpha ={\frac {2\pi d}{\lambda }}}$, ${\displaystyle d}$ étant la différence de marche du rayon 2 par rapport au rayon 1. Cette méthode de superposition de signaux sinusoïdaux est, depuis lors, connue sous le nom de Diagramme de Fresnel ou Représentation de Fresnel, faisant intervenir des vecteurs de Fresnel.

Soit deux systèmes d'ondes de même fréquence :

${\displaystyle u_{1}=a_{1}\,\sin 2\pi ({\frac {x}{\lambda }}-\nu t)}$

${\displaystyle u_{2}=a_{2}\,\sin 2\pi ({\frac {x+d}{\lambda }}-\nu t)}$

On peut écrire ${\displaystyle u_{2}}$ sous la forme :

${\displaystyle u_{2}=a_{2}\,(\sin 2\pi ({\frac {x}{\lambda }}-\nu t)\,.\,\cos {\frac {2\pi d}{\lambda }}+\cos 2\pi ({\frac {x}{\lambda }}-\nu t)\,.\,\sin {\frac {2\pi d}{\lambda }})}$

La somme des deux systèmes d'ondes s'écrit :

${\displaystyle U=u_{1}+u_{2}=(a_{1}+a_{2}\cos {\frac {2\pi d}{\lambda }})\,.\,(\sin 2\pi ({\frac {x}{\lambda }}-\nu t)\,+\,a_{2}\,\cos 2\pi ({\frac {x}{\lambda }}-\nu t)\,.\,\sin {\frac {2\pi d}{\lambda }})}$

En représentant les deux ondes par des vecteurs :

Fig.3-Interférence de deux ondes sinusoïdales représentées par des vecteurs

${\displaystyle a_{1}=\|{\overrightarrow {OM}}\|}$

${\displaystyle a_{2}=\|{\overrightarrow {ON}}\|}$

${\displaystyle A=\|{\overrightarrow {OP}}\|}$

${\displaystyle \alpha ={\widehat {MON}}={\frac {2\pi d}{\lambda }}}$

${\displaystyle \phi ={\widehat {MOP}}\,={\frac {2\pi D}{\lambda }}}$

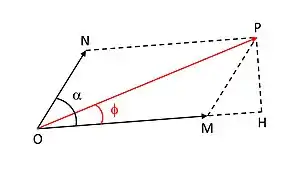
D représentant la différence de marche de l'onde résultante par rapport à l'onde de référence (${\displaystyle u_{1}}$).

Et en posant :

${\displaystyle a_{1}+a_{2}\,cos\alpha \,=\,OH\,=\,OP\,cos\phi \,=\,A\,cos\phi }$

${\displaystyle a_{2}\,sin\alpha \,=\,HP\,=\,OP\,sin\phi \,=\,A\,sin\phi }$

On peut écrire l'équation de l'onde résultante :

${\displaystyle U\,=\,A\,\sin(2\pi ({\frac {x}{\lambda }}-\nu t)+\phi )\,=\,A\,\sin 2\pi ({\frac {x+D}{\lambda }}-\nu t)}$

On peut calculer l'amplitude de l'onde résultante :

${\displaystyle A^{2}\,=\,(a_{1}+a_{2}\,cos\alpha )^{2}+a_{2}^{2}\,sin^{2}\alpha \,=\,a_{1}^{2}+a_{2}^{2}+2\,a_{1}a_{2}\,cos\alpha }$

${\displaystyle A\,=\,{\sqrt {a_{1}^{2}+a_{2}^{2}+2\,a_{1}a_{2}\,cos\alpha }}}$

Et son déphasage par rapport à l'onde de référence :

${\displaystyle tan\phi \,=\,{\frac {sin\phi }{cos\phi }}\,=\,{\frac {a_{2}\,sin\alpha }{a_{1}+a_{2}\,cos\alpha }}}$

« Il résulte de cette formule générale que l'intensité des vibrations de la lumière totale est égale à la somme de celles des deux faisceaux constituans dans le cas de l'accord parfait, à leur différence quand ils discordent complètement, et enfin à la racine carrée de la somme de leurs carrés lorsque leurs vibrations correspondantes sont à un quart d'ondulation les unes des autres[57]. » C'est-à-dire que :

• quand ${\displaystyle d\,=\,\lambda }$ ou, de façon équivalente, ${\displaystyle \alpha \,=\,2\,\pi }$, l'amplitude de l'onde résultante est : ${\displaystyle A\,=\,a_{1}\,+\,a_{2}}$ et elle est en phase avec l'onde de référence.
• quand ${\displaystyle d\,=\,{\frac {\lambda }{2}}}$ ou, de façon équivalente, ${\displaystyle \alpha \,=\,\pi }$, l'amplitude de l'onde résultante est : ${\displaystyle A\,=\,|a_{1}\,-\,a_{2}|}$ et elle est soit en phase avec l'onde de référence si ${\displaystyle a_{1}>a_{2}}$, soit en opposition de phase si ${\displaystyle a_{1}<a_{2}}$.
• quand ${\displaystyle d\,=\,{\frac {\lambda }{4}}}$ ou, de façon équivalente, ${\displaystyle \alpha \,=\,{\frac {\pi }{2}}}$, l'amplitude de l'onde résultante est : ${\displaystyle A\,=\,{\sqrt {a_{1}^{2}\,+\,a_{2}^{2}}}}$ et son déphasage est donné par ${\displaystyle tan\phi \,=\,{\frac {a_{2}}{a_{1}}}}$

Fresnel remarque qu'en combinant une nouvelle onde avec la résultante des deux premières, on retrouverait une nouvelle résultante du même type que la précédente. Il conclut qu'il est ainsi possible d'établir la résultante d'un nombre quelconque de systèmes d'ondes de même longueur d'onde[58].

Fresnel se propose de « donner une explication satisfaisante et une théorie générale [des phénomènes de la diffraction], dans le système des ondulations, sans le secours d'aucune hypothèse secondaire, et en s'appuyant seulement sur le principe de Huygens et sur celui des interférences[51]. »

Il reformule le principe énoncé par Huygens dans son Traité de la lumière : « L'hypothèse fondamentale peut s'exprimer ainsi : Les vibrations d'une onde lumineuse dans chacun de ses points peuvent être regardées comme la somme des mouvements élémentaires qu'y enverraient au même instant, en agissant isolément, toutes les parties de cette onde considérée dans une quelconque de ses positions antérieures[59]. L'intensité de l'onde primitive étant uniforme [...] cette uniformité se conservera pendant sa marche, si aucune partie de l'onde n'est interceptée ou retardée relativement aux parties contigües, parce que la résultante des mouvements élémentaires [...] sera la même pour tous les points. Mais, si une portion de l'onde est arrêtée par l'interposition d'un corps opaque, alors l'intensité de chaque point variera avec la distance au bord de l'ombre, et ces variations seront surtout sensibles dans le voisinage des rayons tangens[60]. »

Fig.4-Principe de Huygens - Vue en coupe perpendiculaire au bord droit d'un écran opaque.

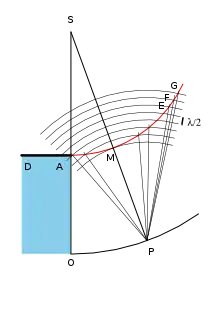
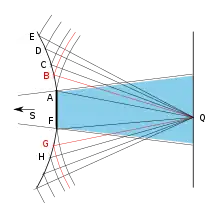
Soit le front d'onde AMG issu d'une source lumineuse ponctuelle S. D'après Huygens, chacun des points de cette surface sphérique est source de lumière diffractée dans toutes les directions. Pour étudier l'amplitude de l'onde lumineuse résultante des contributions des rayons diffusés par le front d'onde vers le point P, en présence d'un écran opaque à bord rectiligne, Fresnel propose d'examiner le parcours des rayons lumineux dans un plan contenant la source et perpendiculaire à l'écran opaque. Il divise le front d'onde en petits arcs à l'aide de cercles centrés en P et dont les rayons diffèrent d'un cercle à l'autre d'une demie longueur d'onde.

Il pose que la contribution de chaque arc au point P est proportionnelle à sa longueur et à un facteur d'obliquité lié à l'angle que forment les rayons diffractés avec le rayon incident direct SP. Mais, « il est aisé de voir que les effets produits par ces rayons se détruisent presque complètement dès qu'ils s'inclinent sensiblement sur la normale, en sorte que ceux qui influent de manière appréciable sur la quantité de lumière que reçoit chaque point P peuvent être regardés comme d'égale intensité[61]. »

Ainsi les rayons fortement obliques comme EP, FP=EP+λ/2 et GP=EP+λ déterminent les arcs EF et FG. Ces deux arcs sont égaux et les rayons qu'ils envoient au point P, presque parallèles. Comme les rayons issus de l'arc EF sont plus courts d'une demie longueur d'onde que ceux qui émanent de l'arc FG, leurs effets se détruisent mutuellement. Pour résoudre le problème, il n'y aura à prendre en compte que les arcs proches de l'écran où les rayons, du fait de la présence de l'écran, ne se détruisent pas mutuellement[62]. Pour replacer le schéma plan dans l'espace, Fresnel imagine que les arcs de cercles dessinés sur la coupe du front d'onde sont la trace de fuseaux délimités par des méridiens sur le front d'onde sphérique. Fresnel n'exploite pas davantage sa construction géométrique pour tenter de déterminer plus précisément la position et l'intensité des franges extérieures. Il résoudra le problème avec un autre dispositif, celui qui mènera à ce que l'on appelle les intégrales de Fresnel.

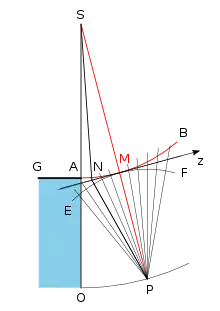
Fresnel applique sa construction géométrique à la détermination des franges intérieures à l'ombre portée d'un fil d'acier. Il trace des rayons QA, QC = QA + λ / 2, QD = QA + 2λ / 2, QE = QA + 3λ / 2... qui délimitent des arcs sur la surface du front d'onde. Il remarque que les rayons issus de l'arc AC sont en opposition de phase avec les rayons issus de l'arc CD. Ils devraient donc en grande partie se neutraliser. Mais les rayons de l'arc CD sont eux-mêmes en opposition de phase avec ceux de l'arc DE. Et ainsi de suite lorsqu'on parcourt le front d'onde au delà de AE[63].

Fig.5 - Franges de diffraction à l'intérieur de l'ombre d'un objet opaque AF

Fresnel en déduit que tous les rayons arrivant en Q et issus du front d'onde se neutralisent à l'exception de ceux qui sont issus de l'arc AC : « Toutes les petites ondes envoyées en P par les éléments de chacun de ces arcs seront en discordance complète avec les ondes élémentaires qui émanent des parties correspondantes des deux arcs entre lesquels il est compris; en sorte que, si tous les arcs étaient égaux, les rayons qu'ils envoient en P se détruiraient mutuellement, à l'exception de l'arc extrême AC, dont les rayons conserveraient la moitié de leur intensité; la moitié de la lumière envoyée par l'arc DC avec lequel il est en discordance complète, étant détruite par l'arc précédent ED[63]. »

Il considère que le rayon QB qu'il nomme le rayon efficace est de longueur QA + λ / 4, ce qui fait que, contrairement à ce qu'il affirme, il n'est pas strictement au milieu de l'arc AC. Il conclut son raisonnement en affirmant que le point B doit être considéré comme la véritable origine des rayons qui arrivent au point Q. Et que c'est le point G, et non le point F, qui doit être pris pour origine des rayons émanant de l'autre côté de l'obstacle. Ces considérations ne changent pas les calculs de position des franges internes présentés précédemment, étant donné que les chemins optiques sont augmentés de la même valeur (λ / 4) des deux côtés[64].

Fig.6 - Figure de diffraction d'une fente lumineuse

Fresnel refait l'expérience, rapportée par Biot, de la diffraction de la lumière par une fente étroite. Il ne trouve pas la même chose et découvre la loi de répartition des franges. Il appelle b la distance de la fente (ou diaphragme) à l'écran d'observation, c, la largeur de la fente et λ, la longueur d'onde.

« La distance entre les points les plus sombres de deux bandes consécutives, prises à droite ou à gauche de l'intervalle clair du milieu, était égale à bλ/c, ou du moins en différait assez peu. Quant à l'intervalle du milieu, j'ai trouvé qu'il variait entre deux limites bλ/c et 2bλ/c, suivant une loi que je n'ai pas encore pu déterminer.

Lorsque le diaphragme est très étroit, et qu'on en reçoit l'ombre à une distance assez considérable, l'intervalle du milieu est toujours, à très peu près, le double des autres intervalles[65]. »

Soit une onde lumineuse issue de S partiellement occultée par un obstacle à bord rectiligne AG, on considère le front d'onde AB à l'endroit où il est partiellement intercepté par l'obstacle. On peut diviser ce front d'onde en une infinité de petites sections de longueur dz qui vont chacune contribuer indépendamment à la lumière au point P. Pour calculer la différence de marche entre un rayon quelconque SNP et le rayon direct SMP, Fresnel trace à partir de P le cercle EF de rayon PM tangent au front d'onde. Il faut considérer que les distances SM et PM sont très grandes par rapport à dz et que les distances sur les arcs AB et EF peuvent être assimilées à la distance sur la tangente Mz aux deux cercles. En plaçant le point N sur cette tangente, en posant SA=SM=a, MP=b, MN=z, l'écart, au point N, entre les deux cercles tangents est la somme des écarts de chaque cercle à la tangente[66] :

Fig.7-Franges de diffraction à l'extérieur de l'ombre d'un écran à bord rectiligne

${\displaystyle \delta =d_{s}+d_{p}}$

${\displaystyle SN^{2}=(a+d_{s})^{2}=a^{2}+2ad_{s}+d_{s}^{2}=a^{2}+z^{2}}$

Le terme ${\displaystyle d_{s}^{2}}$, très petit, peut être négligé :

${\displaystyle 2ad_{s}=z^{2}}$

En répétant le même développement avec ${\displaystyle PN^{2}}$, et en additionnant les deux écarts :

${\displaystyle \delta =d_{s}+d_{p}={\frac {(a+b)z^{2}}{2ab}}}$

Les composantes de l'onde au point N, rapportée à l'onde au point M, sont :

${\displaystyle dz\,\cos {\frac {\pi (a+b)z^{2}}{ab\lambda }}\,\,\,et\,\,\,dz\,\sin {\frac {\pi (a+b)z^{2}}{ab\lambda }}}$

En faisant la somme des composantes semblables de toutes les autres ondelettes secondaires, on a :

${\displaystyle \!\int _{A}^{\infty }\!\cos \left({\frac {\pi (a+b)z^{2}}{ab\lambda }}\right)\,dz\,\,\,et\,\,\,\!\int _{A}^{\infty }\!\sin \left({\frac {\pi (a+b)z^{2}}{ab\lambda }}\right)\,dz}$

Il faut intégrer en deux parties : d'une part de 0 (au point M) à l'infini et, d'autre part, de 0 à x (au point A). La première intégrale converge vers une valeur finie quelle que soit la position de M. La seconde varie en fonction de la distance du point M au point A, bord de l'obstacle, et doit être calculée à l'aide des intégrales de Fresnel normalisées.

Fig.8-Intégrales de Fresnel normalisées

${\displaystyle C(x)=\!\int _{0}^{x}\!\cos \left({\frac {\pi \,v^{2}}{2}}\right)\,dv\,\,\,et\,\,\,S(x)=\!\int _{0}^{x}\!\sin \left({\frac {\pi \,v^{2}}{2}}\right)\,dv\,}$

Fresnel a calculé la valeur des intégrales pour z variant de 0 à 5.1 par incréments de 0.1, et les a publiées dans un tableau. Il indique ensuite comment utiliser le tableau pour trouver l'intensité de la lumière (le carré de l'amplitude) dans la partie non occultée (franges extérieures). Il faut additionner la valeur de l'intégrale entre A et M, et la valeur de l'intégrale de M à l'infini qui vaut 1/2, puis faire la somme des carrés des composantes[67] :

${\displaystyle I_{0}^{e}={\big (}C(x)+0.5{\big )}^{2}+{\big (}S(x)+0.5{\big )}^{2}}$

Fresnel n'a indiqué que plus loin dans son Mémoire comment calculer l'intensité de la lumière diffractée vers l'ombre géométrique[68]. On cite ici le dernier paragraphe de sa note sous pli cacheté déposée le 20 avril 1818 :

« Je terminerai cette note en faisant observer qu'il résulte aussi de la théorie que je viens d'exposer que la lumière qui se répand dans l'ombre des corps doit décroître rapidement à mesure que les rayons s'éloignent de la tangente, et d'une manière graduelle, sans maxima ni minima d'intensité qui forment des franges, toutes les fois du moins que le corps opaque est assez large pour qu'un point quelconque, pris à l'intérieur de son ombre, ne puisse pas recevoir de lumière sensible des ceux côtés à la fois. On peut s'en convaincre aisément avec la table ci-dessus [des intégrales des sinus et des cosinus], en retranchant 1/2 de chacun des nombres correspondant aux intégrales et en faisant la somme de leurs carrés, ce qui donne l'intensité de la lumière répandue dans l'ombre aux points qui correspondent à chaque valeur de z[69]. »

${\displaystyle I_{0}^{i}={\big (}C(x)-0.5{\big )}^{2}+{\big (}S(x)-0.5{\big )}^{2}}$

Fig.9-Franges de diffraction au voisinage de l'ombre géométrique d'un écran à bord droit. Les intensités lumineuses ont été calculées à partir des intégrales normalisées

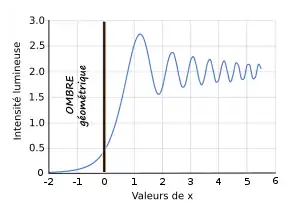
En réalisant ces calculs avec les données normalisées du tableau de Fresnel, on peut tracer la courbe des intensités de la lumière diffractée ${\displaystyle I_{0}=I_{0}^{i}+I_{0}^{e}}$ en fonction de la distance à la limite de l'ombre géométrique (Fig.9).

Cette figure reproduit la courbe calculée par Fresnel et imprimée sur une planche non numérotée à la fin du Mémoire et des deux notes additionnelles, entre la première et la deuxième section des Œuvres complètes. Cette courbe est intitulée Courbe des intensités de lumière en dehors et en dedans de l'ombre géométrique d'un écran indéfiniment étendu. Elle est accompagnée d'un tableau des maxima et des minima des franges extérieures[70]. Les éditeurs indiquent que cette courbe a été retrouvée dans les papiers de Fresnel et n'a pas été précédemment imprimée compte tenu de sa largeur (C'est une feuille pliée quatre fois pour tenir dans le format de l'ouvrage).

On constate que, dans la partie non occultée, l'intensité de la lumière varie autour d'une valeur qui serait celle de la lumière en absence d'écran opaque. On constate aussi que la lumière décroît rapidement de façon continue dans l'ombre géométrique.

Dans son mémoire définitif soumis pour le prix de l'académie, Fresnel détaille le passage des intégrales normalisées aux intégrales issues des déductions géométriques[71] :

${\displaystyle \!\int _{0}^{y}\!\cos \left({\frac {\pi (a+b)z^{2}}{ab\lambda }}\right)\,dz}$

En posant :

${\displaystyle q\,=\,\pi /2\,\,\,\,\,et\,\,\,\,2q{\frac {(a+b)z^{2}}{ab\lambda }}\,=\,qv^{2}}$

On obtient :

${\displaystyle z\,=\,v{\sqrt {\frac {ab\lambda }{2(a+b)}}}\,\,\,\Longrightarrow \,\,\,dz\,=\,dv\,{\sqrt {\frac {ab\lambda }{2(a+b)}}}}$

D'où :

${\displaystyle \!\int _{0}^{y}\!\cos \left({\frac {\pi (a+b)z^{2}}{ab\lambda }}\right)\,dz\,=\,{\sqrt {\frac {ab\lambda }{2(a+b)}}}\!\int _{0}^{x}\!\cos(qv^{2})\,dv}$

L'addition des carrés des composantes permet d'obtenir l'intensité de la lumière :

${\displaystyle I={\frac {ab\lambda }{2a(a+b)}}{\big (}(C(x)+0.5{\big )}^{2}+(S(x)+0.5)^{2}{\big )}\,=\,{\frac {ab\lambda }{2a(a+b)}}\,I_{0}^{e}}$

L'intensité de la lumière est donc obtenue en multipliant par un coefficient dépendant des conditions expérimentales la valeur de l'intensité données par les intégrales normalisées.

La position relative des franges par rapport au bord de l'ombre géométrique reste la même que pour les intégrales normalisées. Pour avoir la position réelle du point P par rapport au point O, il faut mettre en jeu l'homothétie :

${\displaystyle {\frac {AM}{SA}}\,=\,{\frac {OP}{SP}}}$

En posant AM=y et OP=p :

${\displaystyle {\frac {y}{a}}\,=\,{\frac {p}{a+b}}}$

D'autre part, au niveau des bornes d'intégration :

${\displaystyle z\,=\,v{\sqrt {\frac {ab\lambda }{2(a+b)}}}\,\,\,\Longrightarrow \,\,\,y\,=\,x{\sqrt {\frac {ab\lambda }{2(a+b)}}}}$

D'où :

${\displaystyle p\,=\,x\,{\frac {a+b}{a}}{\sqrt {\frac {ab\lambda }{2(a+b)}}}\,=\,x\,{\sqrt {\frac {(a+b)b\lambda }{2a}}}}$

Fig.10-Zones de Fresnel vues depuis l'axe de propagation de la lumière. Toutes les zones sont d'égale surface.

Pour son mémoire soumis à l'Académie en 1818, Fresnel n'avait étudié que la diffraction provoquée par des objets rectilignes, soit un fil, soit une fente, soit un écran à bord droit. À la suite de l'observation de Poisson et de la vérification faite par Arago, Fresnel a étendu son étude à la diffraction par des ouvertures et des écrans circulaires. Ces travaux sont rapportés dans une note publiée à la suite du Mémoire et intitulée: Calcul de l'intensité de la lumière au centre de l'ombre d'un écran et d'une ouverture circulaires éclairés par un point radieux[72]. Il développe alors le concept de zones sphériques ou d'anneaux qu'il avait introduits dans son Mémoire sans l'exploiter. C'est sur ce concept que Max Born et al. dans leur ouvrage Principles of optics, établissent l'équation de la diffraction à partir des zones de Fresnel[73]. Le calcul de la résultante des ondelettes de Huygens convergeant vers le point P, basé sur les zones de Fresnel, est présenté dans l'article Principe de Huygens-Fresnel.

Fresnel commence par étudier la lumière, issue d'une source ponctuelle S, qui parvient en un point P à travers un écran perpendiculaire à l'axe SP, percé d'une petite ouverture circulaire centrée sur SP. Il propose de subdiviser l'ouverture avec des cercles concentriques dont les rayons sont proportionnels aux racines carrées des nombres entiers 1, 2, 3, 4... de telle sorte que la surface des cercles successifs soient proportionnelles à 1, 2, 3, 4... La surface des anneaux définis par deux cercles consécutifs ainsi que le cercle central auront la même surface. Lorsque l'ouverture est illuminée, la même quantité de lumière traverse chaque anneau. Supposons que la différence de marche entre le rayon central et les rayons passant pas le bord de l'ouverture soit égale à un nombre entier de demies longueurs d'onde. Si ce nombre est pair, « il est aisé de voir qu'alors toutes les ondulations élémentaires qui arrivent au centre de l'ombre se détruisent mutuellement... Le centre de la projection de l'ouverture sera privé de lumière. Il en recevra au contraire la plus grande quantité possible quand la différence de marche entre le rayon central et les rayons extrêmes contiendra un nombre impair de demi-ondulations, puisque alors une de ces divisions restera toute entière pour l'éclairer[74]. »

On considère que l'ouverture est infiniment large. Fresnel modifie le raisonnement précédent. Il ne faut plus additionner les contributions lumineuses émises par des anneaux entiers. « Il est bien plus rigoureux de dire que les vibrations qui émanent de chaque anneau sont détruites par la moitié des [amplitudes] qu'apportent les rayons de l'anneau qui le précède et de celui qui le suit[74]. » Le terme vitesses absolues utilisé par Fresnel a été remplacé ci-dessus par amplitudes. Ce nouveau mode de calcul ne modifie par les résultats précédents établis dans le cas d'une ouverture circulaire de dimensions finies.

Si l'ouverture est infiniment grande, on peut regarder comme nulle la contribution des anneaux extrêmes compte tenu de leur excessive inclinaison, comme il a été établi précédemment dans le Mémoire (Fig.4). Le centre de la zone éclairée ne sera plus illuminé que par la lumière qui viendra de la moitié du cercle central. Comme l'intensité de la lumière est égale au carré de l'amplitude, on trouve le résultat paradoxal suivant : lorsqu'il n'y a pas d'écran, l'intensité lumineuse est quatre fois plus faible qu'au centre de la projection d'une petite ouverture dont le diamètre est tel qu'il existe une différence de marche égale à un nombre impair de demies longueurs d'onde entre l'axe et les rayons extrêmes.

Si on applique le nouveau mode de calcul au cas d'une ouverture circulaire finie (Fig.12) de rayon OA=OB=r, la différence de marche entre le rayon axial SP et les rayons SAP passant au bord de l'ouverture est égale à :

${\displaystyle d={\frac {(a+b)r^{2}}{2ab}}}$

avec a=SO et b=OP, les distances du point lumineux à l'écran et de l'écran au point d'observation.

Les minima de lumière seront trouvés pour les différences de marche :

${\displaystyle d={\frac {(a+b)r^{2}}{ab}}=2n\lambda }$

et les maxima, pour :

${\displaystyle d={\frac {(a+b)r^{2}}{ab}}=(2n+1)\lambda }$

Fresnel indique qu'il a vérifié l'exactitude de ces formules en employant la lumière rouge qu'il a utilisée précédemment. Pour les valeurs satisfaisant à la première équation, « on apercevait comme une tache d'encre au centre de l'ouverture circulaire, tandis que ce même point paraissait atteindre son maximum de clarté aux distances déduites de la seconde équation[75]. »

« Les raisonnements que nous avons faits pour le cas d'une ouverture circulaire peuvent s'appliquer à un écran circulaire, et donner une démonstration bien simple du théorème singulier que M. Poisson avait déduit des intégrales générales[75]. »

Fig.11-Diffraction de la lumière
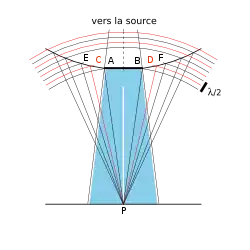
par un petit disque
On a représenté les sphères centrées en P, et dont les rayons consécutifs diffèrent de λ/2, qui dessinent sur la surface du front d'onde sphérique les zones de Fresnel (en noir). Ces zones sont divisées en deux par les cercles rouges.

Fresnel reprend le schéma descriptif qu'il avait employé pour décrire les franges apparaissant dans l'ombre d'un corps rectiligne (Fig.5). Cependant l'objet opaque AB n'est plus un objet rectiligne mais est constitué d'un petit disque. Le dispositif a donc une symétrie de révolution autour de l'axe joignant la source, le centre du disque et le point d'observation P au centre de l'ombre portée. Les arcs dessinés sur la surface du front d'onde sphérique représentent donc la vue en coupe de zones sphériques, appelées Zones de Fresnel. Il applique le même raisonnement que précédemment. Les rayons de chaque zone couvrant un écart d'une demie longueur d'onde entre les rayons qui la bordent sont détruits par la moitié les rayons issus des zones qui l'encadrent. D'autre part, la contribution des zones extrêmes éloignées du disque est considérée comme nulle, compte tenu de leur inclinaison. Il ne reste donc plus que la demie zone AC-BD jouxtant le périmètre de l'obstacle qui contribue à l'éclairement du point au centre de l'ombre portée.

La zone à la périphérie immédiate du disque opaque a la même surface que le cercle élémentaire central. Le centre de l'ombre portée d'un disque reçoit donc la même quantité de lumière que s'il n'y avait pas d'écran. Cet éclairement ne dépend ni de la distance à l'écran, ni de la longueur d'onde. On doit donc pouvoir l'observer en lumière blanche. « C'est ce que M. Arago a vérifié sur l'ombre d'un écran de 2 millimètres de diamètre[38]. »

« Il n'en est pas de même du centre de la projection d'une ouverture circulaire éclairée par un point lumineux; elle présente souvent dans la lumière blanche les plus vives couleurs, couleurs qui changent avec le diamètre de cette ouverture et la distance au point lumineux ou au carton sur lequel on reçoit [la lumière]. La vivacité de ces teintes tient à ce qu'il y a destruction totale de chacune des espèces de rayons colorés qui composent la lumière blanche; ce qui laisse mieux dominer la couleur des autres[38]. »

Fresnel s'applique a établir l'équation qui régit la variation d'intensité de la lumière sur l'axe en fonction de la longueur d'onde et de la distance SO=a, de la source à l'ouverture, et OP=b, de l'ouverture au point d'observation (Fig.12). Il reprend la démarche qu'il a employée pour établir ses intégrales dans les cas de l'ombre d'un écran à bord droit. La différence de marche entre le rayon direct et les rayons passant à la distance OM=z du centre de l'ouverture AB sera :

${\displaystyle d={\frac {(a+b)z^{2}}{2ab}}}$

La surface d'un petit anneau élémentaire de largeur dz qui passe par le point M est égale à ${\displaystyle 2\pi z\,dz}$. La résultante de toutes les ondes envoyées de toutes les zones élémentaires se répartit en deux composantes orthogonales qui s'intègrent facilement, ${\displaystyle 2z\,dz}$ étant la dérivée de ${\displaystyle z^{2}}$:

Fig.12-Diffraction de la lumière
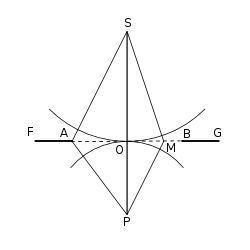
par une ouverture circulaire

${\displaystyle \!\int _{0}^{r}\!\cos {\frac {\pi (a+b)z^{2}}{ab\lambda }}\,2\pi z\,dz\,=\,{\frac {ab\lambda }{a+b}}\sin {\frac {\pi (a+b)r^{2}}{ab\lambda }}}$

${\displaystyle \!\int _{0}^{r}\!\sin {\frac {\pi (a+b)z^{2}}{ab\lambda }}\,2\pi z\,dz=\,{\frac {ab\lambda }{a+b}}{\big (}1-\cos {\frac {\pi (a+b)r^{2}}{ab\lambda }}{\big )}}$

L'intensité de la lumière est égale à la somme des carrés des amplitudes des composantes :

${\displaystyle I\,=\,2\,{\big (}{\frac {ab\lambda }{a+b}}{\big )}^{2}\,{\big (}1-\cos {\frac {\pi (a+b)r^{2}}{ab\lambda }}{\big )}}$

Fresnel procède à une normalisation qui aboutit à la formule suivante :

${\displaystyle I\,=\,{\frac {2}{(a+b)^{2}}}\,{\big (}1-\cos {\frac {\pi (a+b)r^{2}}{ab\lambda }}{\big )}}$

Les maxima doivent se trouver pour ${\displaystyle \cos {\frac {\pi (a+b)r^{2}}{ab\lambda }}=-1}$, soit pour une différence de marche de :

${\displaystyle d={\frac {(a+b)r^{2}}{ab}}=(2n+1)\lambda }$

Les minima doivent se trouver lorsque ${\displaystyle I=0}$, soit pour ${\displaystyle \cos {\frac {\pi (a+b)r^{2}}{ab\lambda }}=1}$ ou pour une différence de marche de :

${\displaystyle d={\frac {(a+b)r^{2}}{ab}}=2n\lambda }$

Le premier minimum doit se trouver, pour n=1, à la distance de l'ouverture :

${\displaystyle b={\frac {ar^{2}}{2a\lambda -r^{2}}}}$

Fresnel rapporte avoir vérifié expérimentalement cette loi. En lumière rouge, il a bien trouvé une extinction complète à une distance de l'ouverture b = 987 mm, avec les paramètres suivant:

• a = 4,000 m
• r = 1,005 mm
• λ = 638 nm

En lumière blanche, il a observé, au même point, que la lumière était de couleur bleu clair. Il termine sa note en comparant les couleurs observées sur l'axe d'une ouverture circulaire avec les couleurs des anneaux de Newton.

• Principe de Huygens-Fresnel
• Représentation de Fresnel
• Spirale de Fresnel
• Diffraction de Fresnel
• Coefficients de Fresnel