Traité de la lumière (Huygens)
Dans son Traité de la lumière, écrit à Paris en 1678 mais publié douze ans plus tard lorsqu'il réside aux Pays-Bas, Christian Huygens expose ses conceptions sur la nature de la lumière qui permettent d'expliquer les lois de l'optique géométrique établies par René Descartes. À la différence d'Isaac Newton qui pensait que la lumière était composée de particules émises par la source lumineuse qui venaient frapper l'œil de l'observateur, Huygens conçoit la lumière comme formée d'ondes sphériques qui se propagent dans l'espace à la manière des ondes sonores. De plus il propose que chaque point d'un front d'onde soit lui-même origine d'une onde sphérique secondaire.
| Traité de la lumière (Huygens) | |
 Édition originale de 1690 | |
| Auteur | Christian Huygens |
|---|---|
| Pays | Pays-Bas / France |
| Version originale | |
| Langue | Français |
| Titre | Traité de la lumière |
| Lieu de parution | Leyde |
| Date de parution | 1690 |
« Je m'étonne ... que personne ait encore expliqué probablement [de façon probante] ces premiers et notables phénomènes de la lumière, savoir pourquoi elle ne s'étend [elle ne se propage] que suivant des lignes droites et comment les rayons visuels, venant d'une infinité de divers endroits se croisent sans s'empêcher en rien les uns les autres[1]. »
Milieu de propagation
Dans le premier chapitre intitulé Des rayons directement étendus, il décrit la lumière comme un ébranlement qui se déplace dans un milieu matériel, de nature inconnue qu'il appelle éthérée et qui est différente de celle qui propage le son. Cette matière éthérée est composée de particules de matière élastiques qui s'entrechoquent selon Les lois des choc des corps, ouvrage qu'il a publié en 1669. Dans le troisième chapitre, De la réfraction, il s'interroge sur la façon dont la lumière se propage dans les liquides et dans les solides transparents. En ce qui concerne les liquides, il n'y a pas de problème à concevoir que les particules du liquide puisse bouger et transmettre la perturbation lumineuse.
Par contre, que se passe-t-il dans les solides comme le verre ou les minéraux translucides? Il considère que la structure de la matière solide est atomique : « cette solidité n'est pas telle qu'elle nous paraît, étant probable que ces corps sont plutôt composés de particules qui ne sont que posées les unes auprès des autres [...] car leur rareté [leur faible densité] paraît par la facilité avec laquelle y passe la matière des tourbillon de l'aimant, ou celle qui cause la pesanteur [...] Il reste donc que ce soit, comme il a été dit, des assemblages de particules qui se touchent sans composer un solide continu[2]. » Les ondes de lumière peuvent donc passer d'une particule à l'autre sans vraiment les faire bouger de leur place.
Une seconde manière d'envisager le problème de la pénétration de la lumière dans les solides ou les liquides est de considérer que ce ne sont pas les particules du milieu transparent qui transmettent la lumière mais les particules de la matière éthérée qui imprègnent les interstices de la matière solide ou liquide, ou même le vide puisque la lumière traverse le vide créé en haut du baromètre de Torricelli. « La rareté des corps transparents étant donc telle que nous avons dit, l'on conçoit aisément que les ondes puissent être continuées dans la matière éthérée qui emplit les interstices des particules[3]. » Enfin, Huygens envisage un troisième type de propagation qui serait une combinaison des deux premiers.
Vitesse de la lumière

Huygens reprend la conception temporelle de Pierre de Fermat. Il considère que l'ébranlement se déplace nécessairement à vitesse finie, même si elle est très élevée. Ce point est très important car ses démonstrations reposent sur l'équivalence des temps de trajets sur les chemins différents.
Il rapporte que l'astronome danois Ole Christensen Rømer lui a indiqué que la vitesse de la lumière est au moins 100 000 fois plus élevée que la vitesse du son, et peut-être encore 6 fois plus élevée [4]. Dans ce dernier cas, la vitesse trouvée par Rømer (214 000 km/s) était du même ordre de grandeur que la vitesse de la lumière admise aujourd'hui.
Chapitre I - Des rayons directement étendus
Propagation sphérique des ondes lumineuses
« La lumière consiste dans un mouvement de la matière qui se trouve entre nous et le corps lumineux[5] [...] Ce ne saurait être par le transport d'une matière qui, depuis cet objet s'en vient jusqu'à nous ainsi qu'une balle ou une flèche traverse l'air [...] C'est donc d'une autre manière qu'elle s'étend et, ce qui peut conduire à la comprendre, c'est la connaissance que nous avons de l'extension du son dans l'air. Nous savons que par le moyen de l'air, qui est un corps invisible et impalpable, le son s'étend tout alentour du lieu où il a été produit, par un mouvement qui passe successivement d'une partie de l'air à l'autre, et que l'extension de ce mouvement se faisant également vite de tous côtés, il se doit former comme des surfaces sphériques qui s'élargissent toujours plus et viennent frapper notre oreille. Or il n'y a point de doute que la lumière en parviennent aussi depuis le corps lumineux jusqu'à nous par quelque mouvement imprimé à la matière qui est entre deux. [...] Il s'en suivra que ce mouvement imprimé à la matière est successif et que, par conséquent, il s'étend, ainsi que celui du son, par des surfaces et des ondes sphériques; car je les appelles ondes, à la ressemblance de celles que l'on voit se former dans l'eau quand on y jette une pierre...[6] » « Il faut considérer encore plus particulièrement l'origine de ces ondes et la manière dont elles s'étendent... Chaque petit endroit d'un corps lumineux, comme le Soleil, une chandelle, ou un charbon ardent, engendre ses ondes, dont cet endroit est le centre[7]. »
Ondelettes secondaires

« Il y a encore à considérer dans l'émanation de ces ondes, que chaque particule de la matière dans laquelle une onde s'étend, ne doit pas communiquer son mouvement seulement à la particule prochaine, qui est dans la ligne droite tirée du point lumineux, mais qu'elle en donne nécessairement à toutes les autres qui la touchent et qui s'opposent à son mouvement. De sorte qu'il faut, qu'autour de chaque particule, il se fasse une onde dont cette particule soit le centre[8][...] On verra dans la suite que toutes les propriétés de la lumière, et tout ce qui appartient à sa réflexion et à la réfraction, s'explique principalement par ce moyen[9]. » L'ensemble des ondelettes issues de chaque point d'un front d'onde AB forme un nouveau front d'onde CE.
Chapitre II - De la réflexion
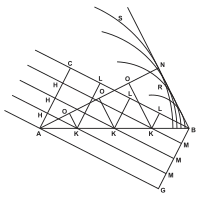
Dans le second chapitre, De la réflexion, Huygens fait une démonstration géométrique de la loi de l'égalité des angles d'incidence et de réflexion. Considérons une onde incidente plane dans le plan de la figure et une surface réfléchissante perpendiculaire au plan de la figure. Soit le front d'onde AC pris au temps t0 où le rayon de gauche touche le miroir. A un instant ultérieur t1, la partie droite du faisceau CB touchera le miroir en B. Si le miroir n'existait pas, le rayon qui a atteint A au temps t0 aurait poursuivi son parcours en ligne droite et, au temps t1, aurait parcouru une distance AG égale à CB. Mais comme le miroir existe et que la vitesse de propagation de la lumière ne change pas avant et après la réflexion, le rayon réfléchi doit parcourir le même chemin au-dessus du miroir que celui qu'il aurait parcouru si le miroir n'avait pas existé. On trace donc un cercle SNR de rayon AG au dessus du miroir, représentant l'onde sphérique issue du point A.
On fait le même raisonnement pour tous les points K intermédiaires et on trace à partir de chaque point K le cercle de rayon KM correspondant. La ligne BN issue de B et tangente à tous les cercles représente le front de l'onde réfléchie au temps t1. Si on veut comprendre les étapes intermédiaires de la réflexion entre t0 et t1, on doit considérer les fronts d'onde OKL intermédiaires entre AC et BN. Le point de tangence N de la droite BN avec le cercle de centre A définit le rayon AN, réflexion du rayon incident arrivant en A. Comme les triangles rectangles ACB et ABN sont égaux, les angles d'incidence et de réflexion sont aussi égaux.
Chapitre III - De la réfraction
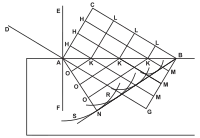
« Passons maintenant à l'explication des effets de la réfraction, en supposant comme nous l'avons fait, le passage des ondes de la lumière à travers les corps transparents et la diminution de vitesse que ces mêmes ondes y souffrent[10]. » On considère une onde lumineuse plane DA se dirigeant du haut à gauche vers la surface AB d'une lame de verre disposée horizontalement. Soit le front d'onde AC au temps t0. Si la vitesse de la lumière était identique au dessus et au dessous du dioptre, le front d'onde serait en GB au temps t1. Supposons que la vitesse dans le verre doit 2/3 de la vitesse de la lumière dans l'air. On dessine un cercle SR de centre A et de rayon égal à 2/3 de AG=CB. On trace à partir de B la tangente au cercle SR. On trace le rayon reliant A au point de tangence N. À partir de tous les points K, on trace les cercles de rayons égaux aux 2/3 de la distance LB correspondante. Tous les cercles sont tangents à la droite BN qui constitue un nouveau front d'onde après que la totalité du faisceau lumineux ait franchi le dioptre.
« d'où il est aisé de reconnaître cette principale propriété des réfractions, savoir que le sinus de l'angle DAE a toujours la même raison [le même rapport] au sinus de l'angle NAF quelle que soit l'inclinaison du rayon DA et que cette raison est la même que celle de la vitesse des ondes dans le diaphane [le milieu transparent] qui est vers AE à leur vitesse dans le diaphane qui est vers AF[11]. »
Jusque là, Huygens ne s'est intéressé qu'aux milieux homogènes et isotropes. Au chapitre 4, intitulé De la réfraction de l'air, il explique les phénomènes optiques provoqués par la différence de densité des couches d'air. Dans ce cas, la vitesse de la lumière n'est pas la même dans toutes les directions.
Chapitre VI. Des figures des corps diaphanes qui servent à la réfraction et à la réflexion
Huygens y donne des méthodes pour dessiner des lentilles (réfraction) ou des miroirs (réflexion) en utilisant ses surfaces d'ondes sphériques.
Conclusion
Dans son Traité de la lumière, Huygens a été capable de fournir une explication qualitative sur la propagation des ondes sphériques et planes, et d'en dériver les lois de la réflexion et de la réfraction. Cependant, bien qu'utilisant des ondes, il n'a pas fait, à proprement parler, d'optique ondulatoire. En particulier, il n'a pas abordé l'hétérogénéité chromatique des ondes mise en évidence par Isaac Newton bien qu'il en ait fait l'expérience malheureuse en construisant son télescope[12].
Les idées de Huygens seront reprises et développées par Augustin Fresnel dans son Mémoire sur la diffraction de la lumière en 1818 pour expliquer les interférences et la diffraction de la lumière[13], ce qui donnera naissance au Principe de Huygens-Fresnel.
Bibliographie
- Christian Huygens, Traité de la lumière, Paris, Gauthier-Villars, coll. « Les Maîtres de la pensée scientifique », , 156 p. (lire en ligne)
Notes et références
- Christian Huygens 1690, p. 2.
- Christian Huygens 1690, p. 35.
- Christian Huygens 1690, p. 38.
- Christian Huygens 1690, p. 7.
- Christian Huygens 1690, p. 3.
- Christian Huygens 1690, p. 4-5.
- Christian Huygens 1690, p. 18.
- Christian Huygens 1690, p. 21.
- Christian Huygens 1690, p. 23.
- Christian Huygens 1690, p. 41.
- Christian Huygens 1690, p. 46.
- David Blanco Laserna, Huygens et la théorie ondulatoire de la lumière, Paris, RBA France, , 165 p. (ISBN 978-2-8237-0257-6), p. 96-98
- Augustin Fresnel, Mémoire sur la diffraction de la lumière, Paris, Académie des Sciences, , 138 p. (lire en ligne)