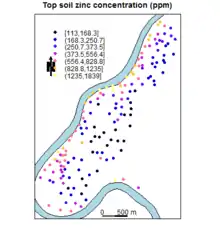
Fouille de données spatiales
La fouille de données spatiales[1] (spatial data mining) est la technique d'exploration de données géographiques, à notre échelle sur terre, mais aussi astronomiques, dont le but est de découvrir des régularités intéressantes dans des données textuelles, diachroniques, ou géométriques telles que vecteurs, trames, graphes. Les données spatiales donnent des informations à des échelles différentes, fournies par des techniques différentes, sous des formats différents, dans une période de temps souvent longue en vue de l'observation des changements. Les volumes sont donc très importants, les données peuvent être imparfaites, bruitées. De plus, les relations entre les données spatiales sont souvent implicites : les relations ensemblistes, topologiques, directionnelles et métriques se rencontrent fréquemment dans cette spécialisation de l'exploration des données. La fouille de données spatiales est donc particulièrement ardue.
L'analyse spatiale participe avec les systèmes d'information géographique à l'analyse exploratoire des données spatiales, mais sa raison d'être constitue la modélisation spatiale[2].
On utilise la fouille de données spatiales pour explorer les données des sciences de la terre, les données cartographiques du crime, celles des recensements, du trafic routier, des foyers de cancer[3], etc.
Histoire
L’histoire de la fouille de données spatiales est liée à celle de la géographie, de l’astronomie et des mathématiques, et au développement de ces disciplines.
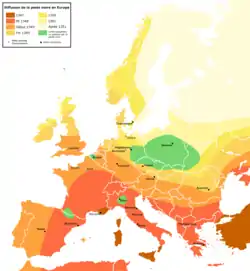
Historiquement, la fouille de données est tout d’abord physique et descriptive. La cartographie a été un des moteurs de celle-ci. En Chine, aux environs des Ve et IVe siècles av. J.-C., les premières cartes indiquent les éléments du relief et des éléments économiques avec une tentative de classification pour les représenter[4]. Du temps de Ptolémée la classification des formes du relief est achevée[5]. En Europe, apparaissent à la fin du IXe siècle les portulans pour lesquels le référencement et la classification des amers étaient nécessaires.
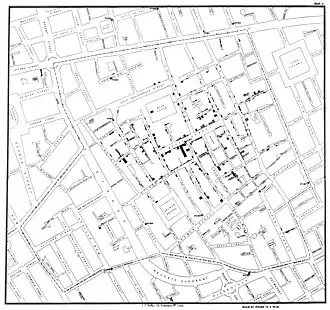
C’est en 1855 qu’apparait peut-être la première fouille de données géographique prédictive. Cette année-là, John Snow recherche les causes de l’épidémie de choléra de la fin de l’année 1854 à Londres, et avec une hypothèse novatrice, et une description précise des foyers de la maladie, prouve que l’eau est un vecteur de contamination et trouve la pompe à eau de Broad Street qui en est la cause[6].
En 1905, les docteurs McKay, Fleming, et Burton font un véritable travail de data miners pour expliquer les taches dentaires de 87,5 % des habitants de Colorado Springs. Analyse des corrélations, avec l’observation des caries notamment, analyse géographique du phénomène, localisant aux alentours de Pikes Peak les enfants ayant des taches, et finalement, en 1931, l’explication par d’autres dentistes du phénomène lié au fluor présent dans les eaux du Colorado bues par les habitants[7].
En 1934, Gehlke et Biehl se rendirent compte, en étudiant les résultats d'un recensement dans la région de Cleveland, qu'un coefficient de corrélation augmentait avec les niveaux d’agrégation, soulevant ainsi un fameux problème connu en analyse géographique à savoir : le problème des unités spatiales modifiables (modifiable areal unit problem (MAUP))[8] - [9].
Le sud-africain Daniel Gerhardus Krige, créateur éponyme, met au point la technique d'interpolation des données spatiales en 1951-1952 connue sous le nom de krigeage (Kriging)[10], formalisée par Georges Matheron à l'École des Mines de Paris en 1962[10].
Le premier SIG, le Système canadien d'information géographique[11] est créé par Roger Tomlinson en 1964-66 et est opérationnel en 1971[12]. La société Environmental Systems Research Institute (ESRI) est fondée en 1969 par Jack et Laura Dangermond à Redlands, Californie[13]. Le 22 février 1978 à 23h44, le premier satellite GPS est lancé par l'US Air Force[14].
Depuis l’avènement de l’exploration de données, les techniques de fouilles de données se sont rapprochées de celles en vigueur dans l'analyse spatiale pour traiter les gros volumes de données, perfectionner les techniques, et diversifier les applications.
Applications
La fouille de données spatiales trouve son application aussi bien dans le domaine public, dans le domaine scientifique que dans le secteur privé. Mais les objectifs ne sont pas identiques. En exploitant les données géographiques, les administrations recherchent plutôt des modèles concernant la population et son bien-être[15] - [Note 1], tandis que l'industrie a des objectifs de rentabilité dans l'implantation d'usines, d'antennes de télécommunication, de panneaux publicitaires, etc.[6] - [16]. Dans le domaine des sciences, l'exploration des données spatiales sert la recherche. En astronomie et en astrophysique, la fouille de données spatiales sert à la classification automatique[17] d'objets spatiaux, ou bien à découvrir des régions dignes d’intérêt, ou des objets rares dans l'immensité de notre univers[18]. En archéologie, les données géographiques et la fouille de données spatiales sont exploitées pour trouver de nouveaux sites[19]. La fouille de données spatiales est utilisée en épidémiologie pour suivre et prévoir la propagation des maladies[20]. Les Sciences de la vie et de la Terre ont aussi recours à cette technique pour évaluer les tendances au cours du temps des modifications de la végétation dans des zones sensibles[21].
Système d'information
Système d'information géographique
« Un Système d'information géographique est un système informatique permettant, à partir de diverses sources, de rassembler et d'organiser, de gérer, d'analyser et de combiner, d'élaborer et de présenter des informations localisées géographiquement, contribuant notamment à la gestion de l'espace. »
— Société française de photogrammétrie et télédétection, 1989
Les SIG ont pour vocation l'acquisition, l'archivage, l'analyse, l'affichage et l'abstraction des données géographiques. L'apport d'un SIG, pour ce qui concerne la fouille de données, est le stockage de l'information géographique numérisée que l'analyste géographe peut ainsi manipuler avec un outil intégré au SIG pour la visualisation par exemple ou bien des outils externes[22] comme GeoDa[23]. Un des SIG les plus connus que l'on trouve sur le marché est ArcGIS[24]; Quantum GIS[25] est un autre SIG que l'on peut citer et qui appartient à la sphère des logiciels libres. Un SIG contient des données alphanumériques et des données spatiales. Dans un SIG, les données sont stockées soit sous format vectoriel, soit sous format raster[26] - [27]. Le format vectoriel gère les points, les lignes et les polygones, les vecteurs sont complétés par des informations alphanumériques. Les données raster sont stockées sous forme de cellules formant une maille. Ces données sont aussi complétées par des données alphanumériques telles que la moyenne, le max, le min, la somme de grandeurs géographiques[28].
Fouilles et techniques de fouille
Les techniques de fouilles de données spatiales s'inspirent de celles de la fouille de données classique, avec une difficulté supplémentaire dans la nature des données qui est celle de la dépendance des données entre elles. Dans la fouille de données classique les variables sont supposées indépendantes, dans la fouille de données spatiales les données sont liées entre elles : une zone est dépendante de ce qui se passe aux alentours, une situation à un instant t dépend de ce qui s'est passé à l'instant t-1. Ces relations peuvent être métriques, topologiques, ou directionnelles[33].
Données aberrantes
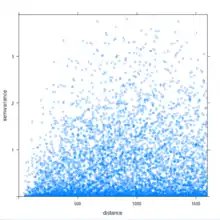
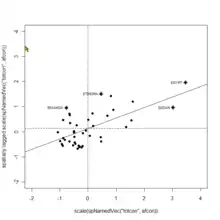
La recherche de données spatiales aberrantes (« outliers ») concerne la recherche de données spatiales dont les valeurs ne sont pas similaires à celles de leurs voisins[34]. On trouve cette technique dans la recherche des incidents de trafic automobiles (accidents, bouchons...)[34]. Les données aberrantes peuvent être repérées par les techniques de visualisation graphiques, ou par des techniques quantitatives. Dans la première catégorie on trouve les nuages de variogrammes et les graphes de dispersions de Moran (« Moran scatterplots »); dans la seconde sont répertoriés les autres graphes de dispersions[35].
Colocalisation
La recherche des colocalisations concerne deux ou plusieurs phénomènes spatiaux reliés entre eux[36]. Plus précisément, Shekhar et al. nous disent que des caractéristiques spatiales booléennes (« Boolean spatial feature ») sont des types d'objets spatiaux présents ou absents en différents lieux. Par exemple, des espèces de plantes, d'animaux, des types de routes, etc. sont des caractéristiques spatiales booléennes. Des schémas de colocalisation sont des sous-ensembles de caractéristiques spatiales booléennes qui sont souvent situées simultanément aux mêmes endroits[37].
Autocorrélation
Les méthodes statistiques supposent que les échantillons ou/et les variables soient non corrélées. En analyse des données spatiales, il arrive que les variables soient autocorrélées, souvent parce que leurs mesures dépendent de la distance[38]. Il est important de savoir si les variables sont autocorrélées ou non. Les tests I de Moran, C de Geary et K de Ripley[39] permettent d'en avoir une connaissance précise[40] - [41].
Interpolation
L'interpolation est la technique consistant à estimer la valeur d'un phénomène au point en fonction des valeurs de ce même phénomène aux points . L'interpolation est nécessaire quand les mesures ne peuvent pas être effectuées partout, comme pour ce qui concerne les précipitations, les températures, la composition des sols, les sources de pollution, la végétation[42].
Les techniques d'interpolation spatiales utilisent des approches déterministes ou des approches stochastiques. Dans la première catégorie, les analystes géographes préfèrent la méthode de Shepard[43], celles des plus proches voisins, ou la pondération inverse de la distance ( « Inverse distance weighting »), ou bien des méthodes de partitionnement comme celle des diagrammes de Voronoï, les techniques de type splines laplaciennes ou de Tendances de surfaces ( « Surface Trend »)[44].
Dans la seconde catégorie, les analystes géographes se tournent vers la régression, la régression locale et le krigeage[44].

Segmentation
Le Clustering[6] - [Note 2] dans le domaine des données spatiales permet de grouper des points selon des caractéristiques communes intéressantes, trouver des sous-trajectoires dans des chemins empruntés, ou bien de regrouper des pixels selon des couleurs qui permettent ensuite de retrouver des éléments naturels (fleuves, mer, forêts)[31].
Plusieurs techniques ayant des buts différents sont utilisées dans la segmentation :
La classification non supervisée spatiale ou segmentation spatiale peut être développée par des méthodes hiérarchiques, des méthodes de partitionnement, d'autres fondées sur la densité de points ou de trajectoires, ou les méthodes fondées sur des grilles[45].
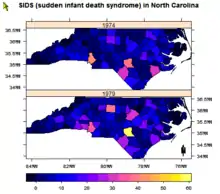
La régionalisation recouvre des techniques dont le but est la classification non supervisée incorporant les contraintes de contiguïté[45]. Plus précisément, ces techniques permettent de regrouper des objets spatiaux dans des régions contiguës tout en optimisant une fonction "objectif"[46].
L'analyse de motifs de points s'intéresse à la détection des points chauds, foyers d'épidémies ou proximité entre centres industriels et apparition de phénomènes tels que maladie, disparition d'espèces[47]...
Classification et Régression
La classification spatiale utilise des modèles pour prédire les classes prédéfinies fondées sur des caractéristiques (variables explicatives) que sont les entités aussi bien que les relations spatiales avec d'autres entités et leurs caractéristiques[48] - [49] - [50]. Autrement dit, les modèles permettent d'estimer les fonctions de classification, en fonction des caractéristiques géospatiales de l'environnement[51].
Parmi les techniques modélisant la dépendance spatiale à des fins de classification ou de régression figurent :
Le Modèle d’Auto-régression simultanée (« Simultaneous AutoRegressive Model » ou « SAR ») est une généralisation du modèle de régression linéaire défini pour tenir compte de l'autocorrélation spatiale dans les problèmes de classification et de régression. Le modèle est utilisé dans les domaines aussi divers que l'économie locale[52], l'analyse d'image[53], l'hydrologie[54], l'analyse criminologique[55], etc.
La Régression géographiquement pondérée (« Geographically Weighted Regression » ou « GWR ») est un autre modèle de régression tenant compte de l'hétérogénéité spatiale [56] - [57].
Les champs aléatoires markoviens forment une autre famille d'outils permettant la classification des phénomènes géolocalisés. Dans ce modèle les relations d'interdépendances sont décrites par un graphe non orienté[51], en tenant compte de la caractéristique markovienne exprimant que la dépendance ne provient que des voisins immédiats[51].
Si définit les classes d'un ensemble de sites ou d'évènements spatiaux est un champ aléatoire markovien, alors les classes sont des variables aléatoires possédant la propriété de Markov qui considère que la classe ne dépend que des voisins de , traduisant ainsi dans le modèle la dépendance spatiale[58] - [59].
Une alternative au modèle d’auto-régression simultanée est le modèle d'Auto-régression conditionnelle fondé sur le concept de champ aléatoire de Markov[60]. Ce modèle est utilisé lorsque les dépendances sont locales avec une dépendance de premier ordre (Est-Ouest/ Nord-Sud) alors que le modèle SAR est plutôt utilisé dans le cas des dépendances de second ordre[61].
Règle d'association
Une règle d'association spatiale est une règle d'association où X ou Y contient des prédicats spatiaux - de types distance, direction, topologique - tels que proche, éloigné, contient, contigu, etc. Effectuer une fouille pour trouver les règles d'associations spatiales, consiste à trouver tous les prédicats, trouver tous les ensembles d'objets ( « itemset » ), et générer les règles fortes ( « strong rules » ), celles qui atteignent le support minimum et dépassent le seuil de confiance[62]. L'exemple tiré de [63]
signifie que si l'objet est une école elle est proche d'un parc avec un taux de confiance de 80 %. School et park sont des objets, est un prédicat.
Règle caractéristique
Limites et problèmes
Le problème des unités spatiales modifiables (modifiable areal unit problem (MAUP)) se pose quand des données spatiales sont collectées au niveau individuel des objets et sont progressivement agrégées dans des groupes préalablement définis. Parfois, les résultats changent au fur et à mesure que le nombre de groupes diminue et l'agrégation augmente. En fait, ce problème peut être décomposé en deux phénomènes distincts : le premier est un problème d'échelle - les résultats se modifient quand les groupes s'agrandissent -, mais aussi un problème d'agrégation - le choix des groupes influe sur les résultats[8].
Comme dans toute exploration de données, la fouille de données spatiale est soumise à la contrainte de la qualité des données. Deux aspects de la qualité des données sont envisagées : la qualité interne et la qualité externe. La première fait référence à la généalogie des données - d'où proviennent-elles, quelles sont les transformations qu'elles ont subies -, à la précision géométrique (positional accuracy) par rapport au terrain, à l'actualité (temporal accuracy) qui met en jeu l'aspect temporel, à la cohérence logique (logical consistency) mettant en jeu la modélisation des données par rapport aux lois de la physique par exemple, et à l'exhaustivité (completeness)[22] - [64]. La seconde fait référence à l'adéquation des données aux besoins des analystes (fitness for use)[65] - [66]. Des données de qualité pour un analyste sont celles qui égalent ou dépassent ses attentes[66].
Notes et références
Notes
- voir par exemple le Géoportail de l'administration française pour la mise à disposition de données géographiques concernant le citoyen et les administrations territoriales.
- voir Glossaire de l'exploration de données pour la définition du Clustering
Références
- (en) « Spatial Database and Spatial Data Mining Research Group : Site officiel », (consulté le )
- [PDF]Catherine Morency, « Étude de méthodes d’analyse spatiale et illustration à l’aide de microdonnées urbaines de la grande région de Montréal », (consulté le )
- [PDF](en) Shashi Shekhar, Pusheng Zhang, « Spatial Data Mining: Accomplishments and Research Needs », (consulté le )
- (en) History of cartography
- (en) www.cosmovisions.com, « Histoire de la géographie » (consulté le )
- [PDF](en) Michael May, « 15th Italian Symposium on Advanced Database Systems - SEBD’07 », (consulté le )
- (en) Colorado Springs Dental Society, « History of Dentistry in the Pikes Peak Region », (consulté le )
- [PDF](en) S. Openshaw, « modifiable areal unit problem » (consulté le )
- [PDF]Christiane Weber, Jacky Hirsch et Aziz Serradj, « Répartition de la Population et Structure Spatiale de Référence » (consulté le )
- Yves Gratton, « Le Krigeage : la Méthode Optimale d’Interpolation Spatiale » (consulté le )
- Guarnieri et Garbolino 2003, p. 43
- « Géomatique et Géographie de l'Environnement : De l'analyse spatiale à la modélisation prospective[auteur=Martin Paegelow » (consulté le ), p. 31
- (en) NAVSTAR, « NAVSTAR GPS 1-1 - Summary », (consulté le )
- (en) ESRI, « Esri History » (consulté le )
- [PDF]François Salgé, « Politique de l'information géographique en France », (consulté le )
- [PDF](en) Paul Duke, « Geospatial Data Mining for Market Intelligence », (consulté le )
- [PDF](en) Oleg Malkov, Leonid Kalinichenko, Marat D. Kazanov, Edouard Oblak, « Data Mining in Astronomy: Classification of Eclipsing Binaries », (consulté le )
- [PDF](en) Alessandro De Angelis, Marco Frailis, Vito Roberto, « Data Management and Mining in Astrophysical Databases », (consulté le )
- (en) GIS in archaeology
- [PDF](en) Chris Bailey-Kellogg, Naren Ramakrishnan, Madhav V. Marathe, « Spatial Data Mining to Support Pandemic Preparedness », (consulté le )
- [PDF](en) Xi-yong HOU, Lei Han, Meng GAO, Xiao-li BI, Ming-ming ZHU, « Application of Spatio-temporal Data Mining and Knowledge Discovery for Detection of Vegetation Degradation », (consulté le )
- [PDF]Sylvain Bard, « Méthode d'évaluation de la qualité des données géographiques généralisées » (consulté le )
- [PDF](en) Luc Anselin, Ibnu Syabri, Youngihn Kho, « GeoDa: An Introduction to Spatial Data Analysis » (consulté le )
- (en) ESRI, « ArcGIS » (consulté le )
- la communauté QGIS, « Quantum GIS » (consulté le )
- CRDP Versailles, « Les Systèmes d’Information Géographiques libres » (consulté le )
- [PDF]Laetitia Perrier Brusle, « SIG : Théorie, définition, applications » (consulté le )
- coastlearn, « Formats raster et vectoriel » (consulté le )
- [PDF](en) Jiawei Han, Krzysztof Koperski, Nebojsa Stefanovic, « GeoMiner : A System Protoype for Spatial Data Mining » (consulté le )
- [PDF](en) A. Komarov, O. Chertov, G. Andrienko, N. Andrienko, A. Mikhailov, P. Gatalsky, « DESCARTES & EFIMOD: An Integrated System for Simulation Modelling and Exploration Data Analysis for Decision Support in Sustainable Forestry » (consulté le )
- [PDF](en) Petr Kuba, « Data Structures for Spatial Data Mining » (consulté le )
- [PDF](en) Michael May, Alexandre Savinov, « An architecture for the SPIN! spatial data mining platform » (consulté le )
- [PDF]Nadjim Chelghoum, Karine Zeitouni, Thierry Laugier, Annie Fiandrino,Lionel Loubersac, « Fouille de données spatiales : Approche basée sur la programmation logique inductive » (consulté le )
- (en)[PDF]Chang Tien Lu, « « A Unified approach to spatial outliers detection » » (consulté le )
- (en)[PDF]Shashi Shekhar, Pusheng Zhang, Yan Huang, Ranga Raju Vatsavai, « « Trends in Spatial Data Mining » » (consulté le )
- [PDF](en) Yan Huang, « « Discovering Spatial Co-location Patterns » », (consulté le )
- [PDF](en) Shashi Shekhar, Pusheng Zhang, Yan Huang, Ranga Raju Vatsavai, « « Trends in Spatial Data Mining » » (consulté le )
- (en) Brian Klinkenberg, « « Spatial Autocorrelation » » (consulté le )
- [PDF](en) Philip M. Dixon, « Ripley’s K function » (consulté le )
- [PDF](en) Arthur J. Lembo, Jr, « « Spatial Autocorrelation » » (consulté le )
- [PDF](en) Roger Bivand, « “The Problem of Spatial Autocorrelation:” forty years on » (consulté le )
- (en) Ferenc Sárközy, « « Gis Functions - Interpolation » » (consulté le )
- (en) ems-i, « Inverse Distance Weighted Interpolation » (consulté le )
- SOM, « Interpolation » (consulté le )
- [PDF](en) (en) Diansheng Guo, Jeremy Mennis, « « Spatial data mining and geographic knowledge discovery—An introduction » » (consulté le )
- Miller et Han 2009, p. 336
- [PDF](en) (en) Anthony C Gatrell, Trevor C Bailey, Peter J Diggle, Barry S Rowlingson, « « Spatial point pattern analysis and its application in geographical epidemiology » » (consulté le )
- (en) « « A Multi-Relational Approach to Spatial Classification » » (consulté le )
- [PDF](en) Deren LI, Shuliang WANG, « « Concepts, Principles and Applications of Spatial Data Mining and Knowledge Discovery » » (consulté le )
- [PDF](en) Richard Frank, Martin Ester, Arno Knobbe, « « A Multi-Relational Approach to Spatial Classification » » (consulté le )
- [PDF](en) Shashi Shekhar, Paul R. Schrater, Ranga R. Vatsavai, Weili Wu, Sanjay Chawla, « Spatial Contextual Classification and Prediction Models for Mining Geospatial Data » (consulté le )
- [PDF](en) Sang-Yeob Lee, « « Spatial Competition in the Retail Gasoline Market: An Equilibrium Approach Using SAR Models » » (consulté le )
- [PDF](en) M. V. Joshi, Subhasis Chaudhuri, « « Zoom Based Super-resolution Through SAR Model Fitting » » (consulté le )
- [PDF](en) Mikhail V. Bolgov, Lars Gottschalk, Irina Krasovskaia, « « Hydrological Models for Environmental Management » » (consulté le )
- [PDF](en) Krista Collins, Colin Babyak, Joanne Moloney, « « Treatment of Spatial Autocorrelation in Geocoded Crime Data » » (consulté le )
- Shashi Shekhar, Michael R. Evans, James M. Kang, Pradeep Mohan, « « Identifying patterns in spatial information: A survey of methods » », (consulté le )
- [PDF](en) Martin Charlton, A Stewart Fotheringham, « « Geographically Weighted Regression White Paper » », (consulté le )
- Miller et Han 2009, p. 129
- [PDF]Foudil Belhad, « Reconstruction Tridimensionnelle à Partir de Coupes Seriées » (consulté le )
- [ppt](en) Haitao, « « Chapter 14 – Spatial autoregressive models » » (consulté le )
- (en) John L. Taylor, « « Spatial statistics models — CAR vs SAR » » (consulté le )
- [PDF](en) Vania_Bogorny">Vania Bogorny, « Enhancing Spatial Association Rule Mining in a Geographic Databases » (consulté le )
- [PDF](en) Krzysztof Koperski, Junas Adhikary, Jiawei Han, « Spatial Data Mining : Progress and Challenges : Survey paper » (consulté le )
- Miller et Han 2009, p. 101
- M. Caprioli, A. Scognamiglio, G. Strisciuglio et E. Tarentino, « Rules and Standards for Spatial Data Quality in GIS Environments » (consulté le )
- Miller et Han 2009, p. 102
Voir aussi
Bibliographie
- (en) Harvey Miller et Jiawei Han, Geographic Data Mining and Knowledge Discovery, Boca Raton, CRC Press, , 458 p. (ISBN 978-1-4200-7397-3).

- (en) Yee Leung, Knowledge Discovery in Spatial Data, Heidelberg, Springer, , 360 p. (ISBN 978-3-6420-2664-5)
- (en) Hillol Kargupta, Jiawei Han, Philip Yu, Rajeev Motwani et Vipin Kumar, Next Generation of Data Mining, CRC Press, , 3e éd., 605 p. (ISBN 978-1-4200-8586-0)
- Franck Guarnieri et Emmanuel Garbolino, Systèmes d'information et risques naturels, Paris, Presses des MINES, , 251 p. (ISBN 978-2-911762-52-9, lire en ligne)
Articles connexes
Liens externes
- Hans-Peter Kriegel, Spatial Data Mining