Diagramme de Venn
Un diagramme de Venn (également appelé diagramme logique) est un diagramme qui montre toutes les relations logiques possibles dans une collection finie de différents ensembles. Les diagrammes de Venn ont été conçus autour de 1880 par John Venn. Ils sont utilisés pour enseigner la théorie des ensembles élémentaires, ainsi que pour illustrer des relations simples en probabilité, logique, statistiques, linguistique et en informatique.
Exemple

Cet exemple est composé de deux ensembles A et B, représentés ici sous forme de cercles colorés. Le cercle orange, l'ensemble A, représente toutes les créatures vivantes bipèdes. Le cercle bleu, l'ensemble B, représente les créatures vivantes qui peuvent voler. Chaque type de créature distincte peut être imaginé comme un point situé dans ce diagramme. Les créatures vivantes qui sont bipèdes et qui peuvent voler —par exemple, les perroquets— sont alors compris dans les deux ensembles, et correspondent ainsi aux points situés dans la région où les cercles bleu et orange se chevauchent.
Les humains et les manchots sont bipèdes, ils sont ainsi dans le cercle orange, mais comme ils ne peuvent pas voler, ils apparaissent dans la partie gauche du cercle orange, où il ne se chevauchent pas avec le cercle bleu. Les moustiques ont six pattes, et volent, de sorte que le point correspondant aux moustiques est placé dans la partie du cercle bleu qui ne se chevauchent pas avec l'orange. Les créatures qui ne sont pas bipèdes et qui ne peuvent pas voler (par exemple, les baleines et les araignées) sont toutes représentées par des points à l'extérieur des deux cercles.
La région combinée des ensembles A et B est appelé l'union de A et B, notée A ∪ B. L'union dans ce cas contient toutes les créatures vivantes qui soit sont bipèdes, soit volent, ou les deux.
La région A et B, où les deux ensembles se chevauchent, est appelé l'intersection de A et B, et est notée A ∩ B. Par exemple, l'intersection des deux ensembles est non vide, parce qu'il y a des points qui représentent des créatures qui sont à la fois situées dans le cercle orange et dans le cercle bleu.
Histoire
Les diagrammes de Venn ont été introduits en 1880 par John Venn dans un article intitulé On the Diagrammatic and Mechanical Representation of Propositions and Reasonings [1]dans le « Philosophical Magazine and Journal of Science[2] », sur les différentes façons de représenter des propositions par des diagrammes[3]. L'utilisation de ces types de diagrammes en logique formelle, selon F. Ruskey et M. Weston, n'est « pas une histoire facile à tracer, mais il est certain que les diagrammes qui sont couramment associés à Venn, en fait, sont apparus beaucoup plus tôt. Ils sont à juste titre associé à Venn, parce qu'il examinait et formalisait leur utilisation, et a été le premier à les généraliser[4] ».
Venn lui-même n'a pas utilisé le terme « diagramme de Venn », mais les a nommé les « cercles Eulériens ». Par exemple, dans la phrase d'ouverture de son article de 1880, Venn écrit : « Les schémas de représentation par diagrammes ont été introduits si couramment dans les traités de logique depuis environ un siècle que l'on peut supposer que beaucoup de lecteurs, même ceux qui n'ont pas fait d'études avancées en logique, connaissent la nature générale et l'objet de tels dessins. De ces schémas, un seul, communément appelés « cercles Eulériens », a été universellement accepté ». Le premier à utiliser le terme de « diagramme de Venn » a été Clarence Irving Lewis en 1918, dans son livre « A Survey of Symbolic Logic »[4].
Les diagrammes de Venn sont très semblables aux diagrammes d'Euler, qui ont été inventés par Leonhard Euler au XVIIIe siècle[5]. M. E. Baron a noté[6] que Leibniz (1646-1716) au XVIIe siècle a produit des diagrammes similaires avant Euler, mais une grande partie de ceux-ci n'ont pas été publiés. Elle observe également, avant Euler, des diagrammes de Raymond Lulle au XIIIe siècle.
Au XXe siècle, les diagrammes de Venn ont encore été développés. D. W. Henderson a montré en 1963 que l'existence d'un diagramme n-Venn avec n fois une symétrie de rotation implique que n est un nombre premier[7]. Il a également montré que des diagrammes de Venn symétriques existent lorsque n = 5 ou 7. En 2002, Peter Hamburger a trouvé des diagrammes de Venn symétriques pour n = 11 et en 2003, Griggs, Killian et Savage ont montré que les diagrammes de Venn symétriques existent pour tous les autres nombres premiers. Ainsi les diagrammes de Venn symétriques existent si et seulement si n est un nombre premier[8].
Les diagrammes de Venn et d'Euler ont été incorporés à l'enseignement de la théorie des ensembles dans le cadre des mathématiques modernes dans les années 1960. Depuis lors, ils ont également été adoptés dans d'autres domaines tels que la lecture[9].
Aperçu
Un diagramme de Venn est construit avec un ensemble de courbes fermées simples tirés dans un plan. Selon Lewis, le « principe de ces diagrammes est que les classes (ou ensembles) peuvent être représentées par des régions avec des relations logiques entretenues les uns avec les autres. Autrement dit, le diagramme laisse d'abord la place pour toute relation possible des classes, et la relation donnée peut alors être spécifiée en indiquant que certaines régions particulières sont nulles ou non nulles[10]. »
Les diagrammes de Venn comprennent normalement des cercles qui se chevauchent. L'intérieur du cercle représente symboliquement les éléments de l'ensemble, tandis que l'extérieur représente les éléments qui ne sont pas compris dans l'ensemble. Par exemple, dans un diagramme de Venn à deux ensembles, un cercle peut représenter le groupe de tous les objets en bois, tandis qu'un autre cercle peut représenter l'ensemble de toutes les tables. La zone de chevauchement, ou l'intersection, représenterait alors l'ensemble de toutes les tables en bois. D'autres formes que les cercles peuvent être employées, comme illustré ci-dessous. Les diagrammes de Venn ne contiennent généralement pas d'informations sur les tailles relatives ou absolues (cardinalité) des ensembles.
Les diagrammes de Venn sont semblables aux diagrammes d'Euler. Cependant, un diagramme de Venn à n ensembles doit contenir 2n zones possibles correspondant au nombre de combinaisons d'inclusion ou d'exclusion dans chacun des ensembles. Dans les diagrammes de Venn, une zone ombrée peut représenter une zone vide, alors que dans un diagramme d'Euler, la zone correspondante est manquante dans le diagramme[11].
La différence entre les diagrammes d'Euler et de Venn peut être observée dans l'exemple suivant. Soit trois ensembles :
Les diagrammes de Venn et d'Euler de ces ensembles sont :
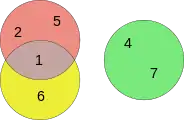 Diagramme d'Euler
Diagramme d'Euler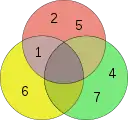 Diagramme de Venn
Diagramme de Venn
Extensions à un grand nombre d'ensembles
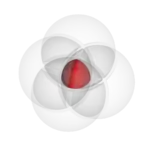
Les diagrammes de Venn représentent généralement deux ou trois ensembles, mais il est possible d'en représenter un plus grand nombre. Ci-dessous, quatre sphères forment le diagramme de Venn d'ordre supérieur qui a la symétrie d'un simplexe et qui peut être représenté visuellement. Les 16 intersections correspondent aux sommets d'un tesseract.
 |

|

|

|
 |
Pour un plus grand nombre d'ensembles, une certaine perte de symétrie est inévitable. Venn était désireux de trouver des « figures symétriques […] élégantes en elles-mêmes[12] », qui représentaient un plus grand nombre d'ensembles, il a alors conçu un diagramme composé de quatre ensembles en utilisant des ellipses (voir ci-dessous). Il a également donné une construction pour les diagrammes de Venn pour tout nombre d'ensembles, où chaque courbe successive qui délimite un ensemble s'entrelace avec les courbes précédentes, en commençant par le diagrammes à trois cercles.
 Construction de Venn pour 4 ensembles
Construction de Venn pour 4 ensembles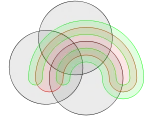 Construction de Venn pour 5 ensembles
Construction de Venn pour 5 ensembles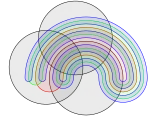 Construction de Venn pour 6 ensembles
Construction de Venn pour 6 ensembles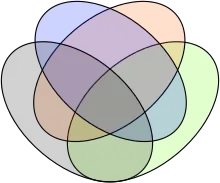 Diagramme de Venn à 4 ensembles utilisant des ellipses
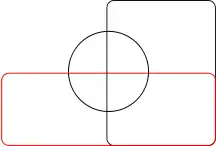
Diagramme de Venn à 4 ensembles utilisant des ellipses Non-exemple : ce diagramme d'Euler n'est pas un diagramme de Venn pour 4 ensembles car il n'a que 14 régions (en comptant l'extérieur) ; il n'existe aucune région où seuls les disques jaune et bleu, ou les disques rouge et vert, se rencontrent.
Non-exemple : ce diagramme d'Euler n'est pas un diagramme de Venn pour 4 ensembles car il n'a que 14 régions (en comptant l'extérieur) ; il n'existe aucune région où seuls les disques jaune et bleu, ou les disques rouge et vert, se rencontrent.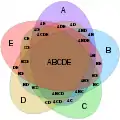 Diagramme de Venn à 5 ensembles utilisant des ellipses congruentes par Branko Grünbaum. Les légendes ont été simplifiées pour une meilleure lisibilité ; par exemple, A représente A ∩ Bc ∩ Cc ∩ Dc ∩ Ec, alors que BCE représente Ac ∩ B ∩ C ∩ Dc ∩ E.
Diagramme de Venn à 5 ensembles utilisant des ellipses congruentes par Branko Grünbaum. Les légendes ont été simplifiées pour une meilleure lisibilité ; par exemple, A représente A ∩ Bc ∩ Cc ∩ Dc ∩ Ec, alors que BCE représente Ac ∩ B ∩ C ∩ Dc ∩ E. Diagramme de Venn à six ensembles utilisant seulement des triangles (version interactive)
Diagramme de Venn à six ensembles utilisant seulement des triangles (version interactive)
Diagrammes de Venn d'Edwards
 Trois ensembles
Trois ensembles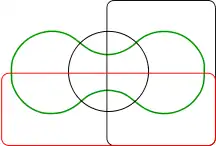 Quatre ensembles
Quatre ensembles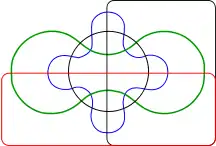 Cinq ensembles
Cinq ensembles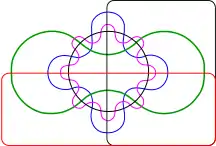 Six ensembles
Six ensembles
A. W. F. Edwards (en) a construit une série de diagrammes de Venn pour un plus grand nombre d'ensembles, en segmentant la surface d'une sphère. Par exemple, trois ensembles peuvent être facilement représentées en prenant trois hémisphères d'une sphère à angle droit (x = 0, y = 0 et z = 0). Une quatrième série peut être ajoutée à la représentation en prenant une courbe similaire à la couture d'une balle de tennis, et ainsi de suite. Ces schémas ont été conçus lors de la conception d'un vitrail à la mémoire de Venn.
Autres diagrammes
Les diagrammes de Venn d'Edwards sont topologiquement équivalents aux diagrammes élaborés par Branko Grünbaum. Ils sont aussi des représentations en 2 dimensions de l'hypercube.
Henry John Stephen Smith a conçu des diagrammes similaires à
Charles Lutwidge Dodgson a conçu un diagramme à cinq ensembles.
Concepts associés

Les diagrammes de Venn correspondent à des tables de vérité pour les propositions , , etc., dans le sens où chaque région du diagramme de Venn correspond à une ligne de la table de vérité[14] - [15].
Notes et références
- John Venn, « On the diagrammatic and mechanical representation of propositions and reasonings », sur Penn Engeneering,
- (en) « The Philosophical Magazine: A Journal of Theoretical Experimental and Applied Physics », Taylor & Francis, (lire en ligne, consulté le )
- Voir :
- (en) J. Venn, « On the diagrammatic and mechanical representation of propositions and reasonings », Philosophical Magazine and Journal of Science, vol. 9, no 59, , p. 1-18 (lire en ligne) ;
- (en) John Venn, « On the employment of geometrical diagrams for the sensible representations of logical propositions », Proc. Cambridge Phil. Soc., vol. 4, , p. 47-59 (lire en ligne).
- F. Ruskey et M. Weston, juin 2005.
- Dans Lettres à une princesse d'Allemagne sur divers sujets de physique et de philosophie d'Euler [Lettres à une princesse allemande sur divers sujets physiques et philosophiques], Académie Impériale des Sciences de Saint-Pétersbourg, 1768, vol. 2, pages 95-126.
- M. E. Baron, mai 1969.
- D. W. Henderson, avril 1963.
- Frank Ruskey, Carla D. Savage et Stan Wagon, décembre 2006.
- Strategies for Reading Comprehension Venn Diagrams
- Clarence Irving Lewis, 1918.
- "Euler Diagrams 2004: Brighton, UK: September 22–23".
- John Venn, 1881.
- Edwards, A. W. F. (2004), Cogwheels of the Mind: The Story of Venn Diagrams, JHU Press, p. 65 (ISBN 9780801874345).
- Ralph P. Grimaldi, 2004.
- (en) D. L. Johnson, Elements of Logic via Numbers and Sets, (lire en ligne), chap. 3.3 (« Laws »).
Voir aussi
Articles connexes
- Connecteur logique
- Octaèdre – Une projection stéréographique d'un octaèdre régulier produit un diagramme de Venn à 3 ensembles.
- Diagramme de Carroll
- Diagrammes d'Euler, de Venn et de Carroll
Bibliographie
- Generalized Venn Diagrams 1987 par E. S. Mahmoodian, avec M. Rezaie et F. Vatan.
- Stewart, Ian (2004). "Ch. 4 Cogwheels of the Mind". Another Fine Math You've Got Me Into. Dover Publications. pp. 51–64. (ISBN 0-486-43181-9).
- Edwards, A.W.F. (2004). Cogwheels of the mind: the story of Venn diagrams. JHU Press. (ISBN 978-0-8018-7434-5).
- Glassner, Andrew (2004). "Venn and Now". Morphs, Mallards, and Montages: Computer-Aided Imagination. Wellesley, MA: A K Peters. pp. 161–184. (ISBN 978-1568812311).
- Ruskey, Khalegh; Ruskey, Frank (27 July 2012). "A New Rose : The First Simple Symmetric 11-Venn Diagram". p. 6452. arXiv: 1207.6452
 . Bibcode:2012arXiv1207.6452M
. Bibcode:2012arXiv1207.6452M
Liens externes
- (en) « Venn diagram », dans Michiel Hazewinkel, Encyclopædia of Mathematics, Springer, (ISBN 978-1556080104, lire en ligne)
- (en) Eric W. Weisstein, « Venn Diagram », sur MathWorld
- Jeu logique de Lewis Carroll – Venn vs. Euler sur Cut-the-knot
- Une Étude sur les diagrammes de Venn
- Génération de diagrammes de Venn pour explorer les Suggestions de résultats sur Google
- Sept ensembles interactifs d'un diagramme de Venn affichant des combinaisons de couleurs
- Diagrammes de Venn à six ensembles fait à partir de triangles
- Postscript pour un diagramme à 9 ensembles de Venn et plus
- Diagramme de Venn dans Excel
- Notices dans des dictionnaires ou encyclopédies généralistes :







