Anomalie dilatométrique

Masse volumique de l'eau en fonction de la température. Le graphe inférieur donne la masse volumique de la glace jusqu'à 0 °C puis celle de l'eau liquide. Le graphe supérieur donne le détail du graphe inférieur pour les masses volumiques de l'eau liquide entre 0 °C et 10 °C. Ce graphe montre le maximum de masse volumique de l'eau liquide autour de 4 °C.

Dans les conditions normales de pression, l'eau atteint sa masse volumique maximale d'environ 1 000 kg·m^-3 à 3,98 °C. En-dessous de 3,98 °C, l'eau commence à se dilater lorsque la température s'abaisse (y compris au cours du gel). Selon les mesures les plus récentes, le maximum de masse volumique de l'eau serait de (999,974 950 ± 0,000 84 kg·m^-3) à une température de 3,983 ± 0,000 67 °C : cet intervalle résulte de la moyenne des résultats obtenus en 2005 par différents instituts de physique allemands.

On peut exprimer la loi de variation de la masse volumique ρ_LF de l’eau exempte d’oxygène dissous en fonction de la température T (exprimée ici en °C) grâce à l'équation du viriel :

${\displaystyle \rho _{\rm {LF}}={\frac {a_{0}+a_{1}T+a_{2}T^{2}+a_{3}T^{3}+a_{4}T^{4}+a_{5}T^{5}}{1+bT}}}$

où les coefficients ont pour valeur :

a₀ = 999,839 52 kg·m^-3 ;

a₁ = 16,952 577 kg·m^-3·°C^-1 ;

a₂ = −7,990 512 7×10^-3 kg·m^-3·°C^-2 ;

a₃ = −4,624 175 7×10^-5 kg·m^-3·°C^-3 ;

a₄ = 1,058 460 1×10^-7 kg·m^-3·°C^-4 ;

a₅ = −2,810 300 6×10^-10 kg·m^-3·°C^-5 ;

et b = 0,016 887 2 °C^-1.

Quant à la masse volumique de l'eau saturée en air dissous, on peut corriger l'équation précédente de la façon suivante[5] :

${\displaystyle \rho _{\text{LG}}=\rho _{\text{LF}}-0{,}004\,612+0{,}000\,106\cdot T}$.

Arrangements moléculaires de la glace (à gauche) et de l'eau (à droite).

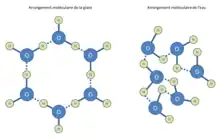
À l’état solide (dans le cas de l'eau on parle alors évidemment de « glace »), la cristallisation aboutit à un empilement ordonné de molécules formant un véritable réseau cristallin. À l’état liquide, la même quantité de molécules occupe en principe un volume plus grand du fait des vitesses élevées des molécules et de l’existence d’un libre parcours moyen. Et puisque le volume augmente, la densité doit diminuer (la masse étant constante). Le chaos devient extrême à l’état gazeux : les molécules s’éloignent en moyenne au maximum de manière à remplir le plus uniformément possible le volume disponible.

L’explication de l’anomalie dilatométrique de l’eau réside dans la formation de chaînes moléculaires par liaison par pont hydrogène. Du fait de la formation spécifique de ces chaînes, l’édifice cristallin solide prend plus de place que les molécules disjointes et mobiles de l’état liquide. La solidification est un processus graduel, ce qui veut dire qu’à l’état liquide il existe déjà des agrégats de molécules d'eau liées. À 3,98 °C l’eau se trouve dans un état où ces agrégats occupent un volume minimum : sa masse volumique est alors maximale. Lorsque l’on continue d’abaisser la température, l’évolution continue de la structure cristalline exige de plus en plus de place ; lorsqu’au contraire on élève la température, l’agitation moléculaire donne naissance à un libre parcours moyen non nul, qui se traduit par une apparente dilatation.

Stratification thermique entre l'été et l'hiver dans un lac.

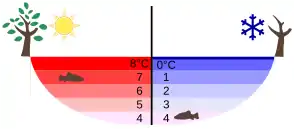
L'anomalie dilatométrique de l'eau joue un rôle considérable pour la survie des espèces lacustres des zones glaciales. Ainsi en raison de cette anomalie dilatométrique, en-dessous d'une température de 4 °C les eaux froides de surface ne convectent plus vers le bas, ce qui empêche le refroidissement des eaux plus profondes. Il y a inversion de la stratification thermique entre l'été et l'hiver (voir illustration ci-contre), donnant, l'hiver, naissance à une couche d'inversion : les eaux profondes restent relativement isothermes, et animaux et plantes peuvent, jusqu'à un certain point, survivre sous la glace.

• Hippolyte Fizeau, « Mémoire sur la dilatation des corps solides par la chaleur », Comptes Rendus des Séances de l'Académie des Sciences, Paris, vol. 62,‎ 1866, p. 1101-1106, 1133-1148.
• B. Dussart, Limnologie – L'étude des eaux continentales, Paris, Gauthier-Villars, 1966 (réimpr. 1992, éd. Boubée), 678 p..
• A. Hade, Nos lacs – les connaître pour mieux les protéger, Éditions Fides, 2002, 360 p..