Transport parallèle
En mathématiques, et plus précisément en géométrie différentielle, le transport parallèle est une façon de définir une relation entre les géométries autour de points le long d'une courbe définie sur une surface, ou plus généralement sur une variété. Si la variété est munie d'une connexion affine (une dérivée covariante ou plus généralement une connexion sur le fibré tangent), alors cette connexion permet de transporter des vecteurs le long des courbes de telle sorte qu'ils restent « parallèles » par rapport à la connexion. Réciproquement, une notion de transport parallèle donne un moyen de relier les géométries de points voisins, et donc, en un certain sens, définit une connexion, qui est l'analogue infinitésimal du transport parallèle.

Le transport parallèle définissant une réalisation locale de la connexion, il définit aussi une réalisation locale de la courbure connue sous le nom d'holonomie. Le théorème d'Ambrose-Singer explicite cette relation entre les deux notions.
D'autres connexions admettent une forme de transport parallèle. Par exemple, une connexion de Koszul sur un fibré vectoriel permet le transport de façon analogue à l'utilisation d'une dérivée covariante. Une connexion d'Ehresmann permet de relever les courbes de la variété à l'espace total du fibré principal, ce qu'on peut interpréter comme un transport parallèle de référentiels.
Transport parallèle sur un fibré vectoriel
Soit M une variété différentielle, E→M un fibré vectoriel de dérivée covariante ∇ et γ: I→M une courbe lisse paramétrée par un intervalle ouvert I. Une section de le long de γ est dite parallèle si
Soit un élément e0 ∈ EP à P = γ(0) ∈ M. Le transport parallèle de e0 le long de γ est l'extension de e0 à une section X le long de γ. Plus précisément, X est la seule section de E le long de γ telle que
- ;
- .
On peut remarquer que, localement, (1) définit une équation différentielle, avec les conditions initiales données par (2). Ainsi, le théorème de Cauchy-Lipschitz garantit l'existence et l'unicité de la solution.
La connexion ∇ définit ainsi une façon de déplacer des éléments des fibres, et plus précisément des isomorphismes linéaires entre les fibres au dessus de points distincts γ(s) et γ(t) de la courbe :
- .
Ces isomorphismes sont les applications de transport parallèle associées à la courbe. Ils dépendent en général du choix de la courbe ; lorsqu'ils n'en dépendent pas, il est alors possible de définir des sections parallèles de E sur M tout entier, mais cela ne se produit que si la courbure de ∇ est nulle.
En particulier, le transport parallèle sur une courbe fermée commençant en un point x définit un automorphisme de l'espace tangent en x, qui n'est pas nécessairement trivial. L'ensemble de ces automorphismes, pour toutes les courbes fermées en x, forme un groupe de transformations appelé le groupe d'holonomie de ∇ en x. Il y a une relation étroite entre ce groupe et la valeur de la courbure de ∇ en x, précisée par le théorème d'Ambrose-Singer.
Reconstruction de la connexion à partir du transport parallèle
Étant donné une dérivée covariante ∇, le transport parallèle le long d'une courbe γ s'obtient en intégrant la condition . Réciproquement, si l'on dispose d'une notion convenable de transport parallèle, on en déduit une connexion par différentiation. Cette approche est essentiellement due à Knebelman, en 1951[1].
Plus précisément, soit, pour chaque courbe γ de la variété, un ensemble d'applications
telles que
- , l'identité de Eγ(s) ;
- ;
- est une fonction « lisse » de γ, s, et t.
La condition 3 est quelque peu délicate à rendre rigoureuse (voir plus bas la discussion concernant le cas des fibrés vectoriels). En particulier, les auteurs modernes comme Shoshichi Kobayashi (en) et Katsumi Nomizu (en) voient généralement le transport parallèle de la connexion comme provenant d'une autre connexion, où la notion de fonction lisse est plus aisément formulée.
Si l'on interprète ces applications comme des transports parallèles , il est possible de retrouver la connexion infinitésimale associée de la manière suivante. Soit γ une courbe différentiable de M d'origine γ(0) et de vecteur tangent initial X = γ′(0). Si V est une section de E sur γ, on pose
Cela définit une connexion ∇, et l'on retrouve Γ comme transport parallèle associé à ∇.
Un cas particulier : le fibré tangent
Soit une variété différentielle. Une connexion sur le fibré tangent de , appelée connexion affine, permet de distinguer une classe de courbes appelées géodésiques (affines)[2]. Une courbe lisse est une géodésique affine si est transportée parallèlement le long de , c'est-à-dire si
En dérivant par rapport au temps, on obtient la forme plus familière :
Transport parallèle en géométrie riemannienne
En géométrie pseudo-riemannienne, une connexion métrique (en) est une connexion dont les applications de transport parallèle préservent le tenseur métrique, c'est-à-dire une connexion telle que pour tout couple de vecteurs de on a :
Prenant la dérivée en , on voit que l'opérateur différentiel associé doit satisfaire une règle du produit par rapport à la métrique :
Géodésiques
Si est une connexion métrique, les géodésiques affines sont les géodésiques usuelles de la géométrie riemannienne, c'est-à-dire les courbes de longueur (localement) minimale. Plus précisément, on remarque d'abord que si est une géodésique (avec intervalle ouvert), la norme de est constante sur , puisque
Appliquant le lemme de Gauss, on en déduit que si est la norme de , la distance induite par la métrique entre deux points de la courbe suffisamment proches et est donnée par
La formule ci-dessus pourrait ne pas être vraie pour les points qui ne sont pas assez proches puisque la géodésique pourrait par exemple s'enrouler autour de la variété (comme dans le cas d'un cylindre).
Généralisations
Le transport parallèle peut être défini de manière plus générale pour d'autres types de connexions, et pas seulement pour celles définies sur un fibré vectoriel. Une de ces généralisations existe pour les connexions principales[3]. Soit P → M un fibré principal sur une variété M sur laquelle opère un groupe de Lie G et une connexion principale (en) ω (c'est-à-dire une 1-forme différentielle à valeurs dans l'algèbre de Lie de G, avec des conditions de compatibilité convenables[4]). Comme pour les fibrés vectoriels, ω définit, pour chaque courbe γ de M, une application
de la fibre au dessus de γ(s) vers celle au dessus de γ(t), qui est un isomorphisme d'espaces homogènes, pour chaque g∈G.
D'autres généralisations du transport parallèle existent. Dans le cas des connexions d'Ehresmann, où la connexion repose sur une notion de « relèvement horizontal (en) » d’espaces tangents, on peut définir un transport parallèle par relèvement horizontaux. Dans le cas des connexions de Cartan (en), qui sont des connexions d'Ehresmann munies de structures supplémentaires, ce transport parallèle peut être vu comme le « roulement » d'un certain « espace modèle (en) » le long d'une courbe de la variété ; ce roulement est appelé un développement, par analogie avec les notions de développée et de courbe développante.
Approximation : l'échelle de Schild
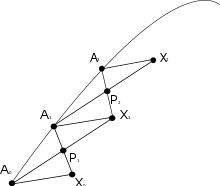
Une approximation discrète du transport parallèle est donnée par l'échelle de Schild (en), qui effectue des pas finis le long de la courbe, et approche les parallélogrammoïdes de Levi-Civita (en) par des parallélogrammes.
Notes et références
- Knebelman 1951, cité par Guggenheimer 1977.
- Kobayashi et Nomizu 1996, chapitre III
- Kobayashi et Nomizu 1996, chapitre II
- De façon précise, ω appartient à et vérifie 1) où Rg est la multiplication à droite par g, et ) ; 2) si et Xξ est le champ de vecteurs sur P associé à ξ en différentiant l'action de G sur P, alors ω(Xξ) = ξ (pour tout ξ).
Voir aussi
Bibliographie
- (en) Heinrich Guggenheimer, Differential Geometry, New York, Dover, , 378 p. (ISBN 0-486-63433-7).
- (en) Knebelman, Spaces of relative parallelism, vol. 53, The Annals of Mathematics, Vol. 53, No. 3, , 387–399 p. (DOI 10.2307/1969562), chap. 3.
- (en) Shoshichi Kobayashi et Katsumi Nomizu, Foundations of Differential Geometry, Volume 1, Wiley-Interscience, , 344 p. (ISBN 0-471-15733-3).
- (en) « Transport parallèle », dans Michiel Hazewinkel, Encyclopædia of Mathematics, Springer, (ISBN 978-1556080104, lire en ligne)
Liens externes
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Parallel transport » (voir la liste des auteurs).
- (en) Démonstration en géométrie sphérique : une applet Java permettant de visualiser le transport parallèle de vecteurs tangents à une sphère.




































