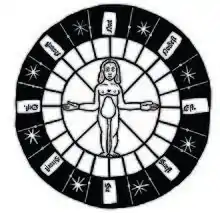
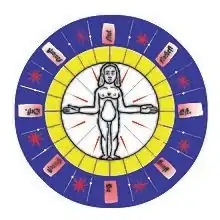
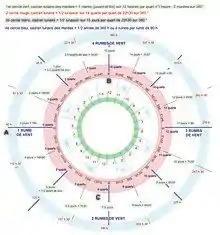
Roue pôle-homme
La roue pôle-homme est un instrument « marinisé » au XVe siècle par les Portugais (roda do homen do polo)[1], qui fournit au marin un cadran des heures, un cadran aux étoiles, un cadran compas, un cadran solaire, un cadran lunaire et un cadran des marées, avec les règlements pour chaque cadran. Il présente une double fonction, en 24 secteurs et 32 aires.
Le Grant Routtier, que Pierre Garcie dit Ferrande[2], termine en 1483, est publié en 1502 et 1520 jusqu’en 1662. Il donne à la communauté maritime française le moyen de naviguer au large. Pierre Garcie rappelle l’importance de cette avancée scientifique maritime : comment naviguer sans voir la terre et sans instrument de marine autre que la roue pôle-homme.
« [J’ai] composé et [t’ai] envoyé le présent livret, qui t’apprendra à reconnaître et connaître les noms des vents et leurs rhumbs, en présupposant toutefois que tu saches, toi ou un autre, distinguer [le cycle de] la Lune [de celui] du Soleil. Le Soleil et la Lune sont les guides et gardiens de tous les braves compagnons qui voguent et naviguent à travers les ondes innombrables de la mer, pour ce qui a trait tant au transport de marchandises qu’à la pêche. Toutefois, bien que le Soleil et la Lune te permettent de reconnaître et connaître les heures - le Soleil, de jour et la Lune, de nuit - j’ai voulu te donner à savoir et reconnaître sans voir ni Soleil ni Lune l’heure de minuit et l’aube du jour. Et tu pourras tout savoir par la figure suivante, sans avoir d’horloge mesurant les heures ou les demies, ni compas, par nuit claire. S’ensuit la figure qui apprend à reconnaître et savoir les heures de nuit, c’est-à-dire minuit et l’aube du jour, sans Soleil ni Lune ni compas, et sans horloge mesurant les heures ou les demies, avec les noms et les rhumbs des vents, ce qui est une chose très délicate et nécessaire pour l’habile et ingénieux métier de la mer. »
— Pierre Garcie dit Ferrande, Le Grant Routtier, f° 2r (p. 3)[2]
Introduction
Le XVe siècle est une période charnière pour la navigation côtière[3]. Celle-ci prend son essor vers le large grâce à l’avancée scientifique.
Elle va bénéficier de deux apports, celui du monde arabe et celui du Portugal (dont Christophe Colomb, 1451 - 1506 est l’éclatant témoignage). Les méthodes des navigations arabes et occidentales ne sont pas des copies identiques. Elles ont, cependant, le point commun d’être le résultat d’une collaboration entre des scientifiques et des marins. La transmission des savoirs scientifiques est affaire de savants, alors que la transmission des techniques est affaire de professionnels. Pierre Garcie dit Ferrande (1441-1502) est un marin français et un savant qui expérimente cette science. Il en fera un trésor avec le premier routier européen, Le Grant Routtier - 1483, 1502 et 1520, viatique indispensable pour tous les marins européens jusqu’au milieu du XVIIe siècle.
Des instruments de navigation marinisés
Avant le XIVe siècle, les instruments d’astronomie sont établis pour un usage à terre. Les arabes, puis les portugais, cherchent à les mariniser. La vraie nouveauté des marins portugais réside dans les instruments utilisés : l’astrolabe nautique, le quadrant de navigation, l'arbalestrille, la roue pôle-homme (ancêtre du nocturlabe)[4].
L'astrolabe, qui mesure la hauteur du Soleil, sera adapté en mer sous une forme très simplifiée, l’astrolabe nautique (en bois au début). En raison du roulis et de la difficulté d’observer le Soleil directement, il sera utilisé à terre, à l’escale. Le marin utilise aussi l’arbalestrille ou bâton de Jacob, sur le bateau, lorsque la mer est calme. La hauteur du Soleil n’est pas fixe dans la durée en raison de la variation journalière de sa déclinaison. Il faut donc impérativement passer par le détour du calcul de la latitude pour pouvoir comparer des valeurs comparables et non plus se contenter du chemin Nord-Sud parcouru. Le calcul est dans les deux sens : si on connaît l’heure, la latitude et la hauteur du Soleil, on a la déclinaison du Soleil ; mais aussi si on connaît l’heure, la déclinaison et la hauteur du Soleil, on a la latitude.
Pour effectuer des mesures astronomiques à bord, il va falloir inventer un nouvel instrument spécifique : le quadrant de navigation. C’est un instrument dérivé du quadrant astronomique, simplifié, qui ne sert qu’à prendre la hauteur de l’astre. On se sert d’un quart de cercle gradué. On vise directement l’étoile selon un des côtés droits du quadrant, un fil à plomb est fixé au centre du cercle et marque la verticale. On lit la hauteur de l’astre visé à l’intersection du fil à plomb et de la graduation sur le secteur circulaire. En fait, on prend, non pas la hauteur, mais la distance zénithale, qui est le complément de cette hauteur. La précision de l’instrument est médiocre et surtout variable selon les mouvements du navire qui influent sur les mouvements du fil à plomb et donc sur la précision de lecture : par expérience de 0,5 à 3 degrés, selon que le temps est calme ou la mer agitée.
Roue pôle-homme
Le quadrant est dérivé d'un instrument ancien, utilisé dans le cadre religieux pour définir la latitude des lieux Saints et l’heure nocturne en vue de l'appel à la prière dans les monastères : la « roue des heures ». Les astronomes vont offrir aux navigateurs un instrument marinisé, la roue pôle-homme, avec une méthode pratique et largement utilisée pour repérer le passage de l’étoile polaire au méridien inférieur ou au méridien supérieur, qui se remarque par le minimum ou le maximum de hauteur de l’astre durant son circuit dans le ciel.
Cet instrument dessiné est une double roue de 24 et 32 secteurs. Sur la 2e couronne (en jaune), que l’on peut appeler un cadran-horloge, le marin lit les 24 secteurs pour 24 heures ou 24 quinzaines. Sur la 1re couronne (en bleu), avec les étoiles (en rouge), la roue définit les 32 aires de vent. Deux étoiles sont séparées par 4 quarts de ¾ d'heure chacun, soit la valeur d’un rhumb. Ces 32 aires de vent délimitent 4 points cardinaux, 8 rhumbs ou points inter-cardinaux. Cette première couronne de la Roue, on peut l’appeler un cadran-compas. Les deux couronnes définissent ainsi une équivalence : chaque rhumb vaut 3 heures (2e couronne) et 4 quarts de ¾ d’heure chacun (1re couronne). Pierre Garcie insiste sur le fait que la rose des vents, à 24 divisions et 32 aires, est à la fois une boussole et une horloge. Quand Pierre Garcie dit que le Soleil est au NE, il ne s’agit pas d’une visée, mais qu’il est 3 heures.
Historique de son développement
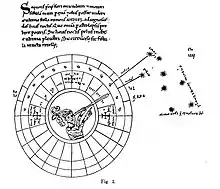
VIIe siècle
L’existence et l’utilisation de la roue pôle-homme sont l’aboutissement d’une recherche scientifique très ancienne, dont la première trace écrite est du VIIe siècle, celle de Sévère Sabok (… ca 659), évêque syriaque : l’astrolabe plan servait surtout à la détermination de l’heure diurne ou nocturne.
L’allusion[1] la plus ancienne que nous connaissions à un instrument du type de la roue pôle-homme est celle de l’horologium nocturnum de Pacificus de Vérone[5] (… ca 844). Ce que l’on sait de cet instrument provient du poème de Pacificus, Spera coeli quater, illustré d’une figure. La plus ancienne représentation date du Xe siècle et se trouve dans un manuscrit de la Bibliothèque du Vatican[6]. Une représentation analogue, datant du XIIe siècle ou XIIIe siècle, apparaît dans un manuscrit conservé à la bibliothèque Marciana de Venise[7]. Ces dessins montrent un observateur visant une étoile ou Polaris à travers un tube optique monté sur un pied. L’extrémité du tube, autour de l’étoile, est entourée d’un disque comprenant trois cercles concentriques, le cercle extérieur étant gradué en 24 heures.
Le manuscrit 235[8] de la Bibliothèque d’Avranches, issu du scriptorium de l’abbaye du Mont-Saint-Michel au XIIe siècle, contient la représentation et la description sommaire d’une roue pôle-homme semblable à l’horologium nocturnum de Pacificus. L’horlogium nocturnum sera diffusé dans tous les lieux monastiques pour poser le début des prières de Laudes à 3 h du matin.
XIe siècle, en Catalogne
.jpg.webp)
Par la suite[1], cette diffusion se fera par les transfuges mozarabes (chrétiens espagnols vivant en Al-Andalus selon l’ancienne foi chrétienne de rite wisigothique). Ils ont été arabisés, à l’apogée de la dynastie Omeyyade de Cordoue. Ces mozarabes, tentés par la vie monastique, ne peuvent la réaliser en terre arabe et gagnent les monastères d’Occident. C’est avec eux qu’est transmise l’étude de la culture arabe par une coopération intellectuelle entre moines occidentaux et moines mozarabes[9]. C’est dans ces monastères catalans que Gerbert d’Aurillac (945…) entre en contact avec les mathématiques arabes. Cet intellectuel deviendra le pape Sylvestre II, mais auparavant, il est le grand responsable du renouveau du quadrivium, c’est-à-dire de l’étude des sciences dans l’enseignement occidental. Il est à l’origine de l’Abaque, la première forme du calcul numérique en Occident et il y introduit les chiffres arabes, sauf le zéro. À la fin d’un manuscrit des Sententiae astrolabii, conservé à Chartres, on trouve une image illustrant l’utilisation d’un instrument de calcul de hauteur de la Polaire. Les savants se succéderont pour améliorer cet instrument :
- 1130-1141, Raymond de Marseille avec un Traité sur l ’ astrolabe, un Liber cursuum planetarum, à partir des acquis de l’astronomie d’Al-Zarqâlluh ;
- 1142, Adélard de Bath traduit les Tables astronomiques (820) d’Al-Khawarizmi, école de Bagdad ;
- 1147, Robert de Chester traduit les Tables astronomiques (929) d’Al-Battani, école de Bagdad ;
- 1150, Moshe et Jacob Ibn Tibbon' à Marseille et Montpellier traduisent des Traités sur l’arithmétique et l’astronomie arabes ;
- 1158-1161, Abraham ibn Ezra, écrit sur les usages des Tables astronomiques et sur un autre traité en hébreu.
- v. 1280, la Carte pisane, de Gênes, est le plus ancien portulan d’origine occidentale connu.
- 1276-1292, Robert Anglès compose le Traité du quadrant.
- 1299, le majorquin Raymond Lulle[10] décrit l’opération d’une horloge nocturne ou Roue des heures par la Polaire, appelé astrolabii nocturni (connu comme Noturlábio). Il écrit dans son Arbor scientiae en 1295 à propos des marins « habent chartam, compassum, acum et stella maris. » Acus c’est l’aiguille, (autrement dit la boussole) ; stella maris, l'Étoile Polaire et son mouvement la Roue polaire.
- 1375, Jehuda Cresques (vers 1350-1427) réalise, avec son père, Abraham Cresques l’Atlas catalan, sur la commande du roi d’Aragon. Vers 1420, Henri le navigateur accueille ce cartographe majorquin, qui devient maître Jaime Ribes « homme très versé dans l’art de naviguer ».
XIIIe siècle, en Occident
La diffusion arabe, espagnole et portugaise gagne les pays qui vont se lancer dans la course aux Grandes Découvertes océaniques[1].
- 1438, le portugais D. Duarte décrit une Roue polaire ou horloge nocturne dans Leal Conselheiro (pt) (1428-1438). Aucune copie de cet instrument n’est connue.
- 1457, l'espagnol Jehuda ibn Verga (en) écrit à Lisbonne un Traité d’astronomie.
- 1472, Joannes de Sacrobosco écrit un Tractatus de Sphaera.
- 1473, Abraham Zacuto, professeur d’astronomie à Salamanque (1474-1492, puis au Portugal dès 1492) commence l’Almanach perpetuum. Il est terminé en 1478, imprimé en 1496 à Leiria, Portugal. Il donne les Tables de déclinaison : la distance du Soleil à l’équateur, c’est-à-dire sa déclinaison.
- 1473-1484, présence de Christophe Colomb au Portugal.
- 1475, Regiomontanus publie les Éphémérides et les Tabula directionum.
Pierre Garcie dit Ferrande (1441-1502)
En France, Pierre Garcie dit Ferrande[2] est le premier français à diffuser son art de la navigation par l'astronomie. Sa publication sera diffusée jusqu'en 1662, tant elle devint indispensable aux marins qui partent en haute mer.
- 1483, Pierre Garcie dit Ferrande signe son manuscrit, Le Routier de la Mer. Il est imprimé en 1502 et prendra pour nom Le Grant Routtier, en 1520. Il sera publié jusqu’en 1662.
- 1484, Martin Behaim arrive à Lisbonne. Il prépare son Erdapfel, le plus vieux globe du monde encore existant, qu'il a conçu pour Nuremberg.
- C’est pour résoudre le problème des Tables de déclinaison à l’usage des marins, que le roi Jean II réunit une commission, Junta dos matematicos do Rei. 1484 ?-1490 ? Elle aura pour mission d’extraire des traités d’astronomie et d’astrologie des tables permettant de prévoir les écarts du Soleil par rapport à l’équateur.
XVe siècle, les voyages océaniques
La recherche scientifique fondamentale et pratique connaîtra un formidable bond avec les voyages océaniques. Peu à peu les instruments de marine, confrontés à leur utilisation sur un bateau vont se perfectionner.
- 1487-1488, Bartolomeu Dias part pour la découverte du cap de Bonne Espérance.
- 1492-1493, Christophe Colomb part pour son premier voyage vers le Nouveau Monde. « Formé à la navigation au milieu du XVe siècle, il a déjà abordé la navigation astronomique. Il connaît et pratique les hauteurs méridiennes de la Polaire, mais sans trop semble-t-il maîtriser le calcul de la latitude. En revanche, il ignore tout des méridiennes de Soleil. Elles ne seront mises au point qu’un peu avant son premier voyage. À cette époque, Christophe Colomb ne réside plus au Portugal et n’a donc pas accès à ces recherches. Il n’en reste pas moins que son journal est l’œuvre d’un professionnel de la mer, un maître de l’estime. C’est la première œuvre centrée sur la technique pratique de la navigation dont nous disposons en Occident. C’ est une source aussi essentielle que celle de son contemporain oriental, Ibn Majid (1430-1500)[3] ».
- 1496, Abraham Zacuto fait imprimer l ’ Almanach Perpetuum. C’est un ensemble de tables de déclinaison[11], reprises des ouvrages de cet astrologue juif. Rédigé d’abord en hébreu, l’Almanach Perpetuum fut traduit en latin par Joseph Vizinho, très probablement Maître Joseph, médecin royal, membre de la Commission installée par le roi, D. João II. Ces tables furent introduites sous les titres de Regimento del sol e del norte et Regimento do Astrolabio e do Quadrante[1]. (Regimento au sens de Règle : Réglement de la Polaire).
- 1503, la traduction du Traité de l’astrolabe de Masha'allah ibn Atharî (astronome musulman, 740-815) par Jean de Séville est imprimée.
- 1509, Règlement de l’astrolabe et Traité de la sphère[12] (Munich)[13]. C’est le premier document connu qui traite de la méthode du calcul des latitudes, d’après la hauteur du Soleil et de la Polaire. Ce Règlement détermine chaque jour la déclinaison, l’emplacement du Soleil et la position de l’étoile polaire ; 1. calcul des latitudes d’après la hauteur du Soleil ; 2. règlement de l’étoile polaire ; 3. liste des latitudes pour les côtes occidentales d’Afrique jusqu’à l’Équateur ; 4. règlement pour évaluer le chemin parcouru par le navire ; 5. calendrier sans indication d’année donnant la position du Soleil dans les signes du zodiaque, sa déclinaison et tables nautiques pour une année bissextile.
- 1514, le Traité de la boussole, par João de Lisboa étudie la déviation de l’aiguille et l’observe à l’aide de l’astrolabe.
- 1516-1518, le Règlement d’Évora[12] traite les mêmes sujets que le Règlement de Munich, ajoutant : 6. le règlement pour déterminer l’heure, la nuit, à l’aide de l’étoile polaire ; 7. le règlement pour déterminer l’heure de la marée haute. Le instruments utilisés sont l’astrolabe, le quadrant et la Roda do Homen do Polo ou roue pôle-homme.
- 1518, Valentim Fernandes publie le Repertório dos Tempos. Il présente la Roue polaire comme horloge nocturne et comme quadrant pour le calcul de la méridienne Nord-Sud. À cette utilisation, Valentim Fernandes va apporter la correction de la déclinaison de la Polaire. À cette époque, l’étoile polaire était éloignée de 3,5° du Pôle, suivant sa place dans le ciel.
- 1520, Fernand de Magellan découvre le détroit de Magalhànes. L’expédition revient en Espagne avec la Victoria en 1522.
- 1520, le manuscrit de Pierre Garcie dit Ferrande (1441-1502) est imprimé en 1520 sous le titre Le Grant Routtier : impression avec 200 pages imprimées, 59 dessins d’amer, la figure de la roue pôle-homme et son utilisation. Ce marin français a reçu de son père espagnol, Jean Ferrande, la science de la navigation hauturière naissante que le Règlement d’Évora a mis en forme pratique. Il est le premier en France à avoir rendu publique la méthode du calcul de l’heure nocturne et celle de la latitude d’un lieu. Dans son ouvrage de 1502, puis surtout de 1520, il propose : le règlement de l’étoile polaire ; la liste des latitudes (distances) des ports et havres ; le règlement pour évaluer le chemin parcouru par le navire ; le règlement pour déterminer l’heure, la nuit, à l’aide de l’étoile polaire ; le calendrier julien et calcul pour le Nombre d’or d’une année et d’une année bissextile ; le calcul de la Nouvelle Lune en début d’année () ; le calcul de l’âge de la Lune et des marées suivant l’établissement du port.
- La recherche scientifique pratique se poursuivra avec Duarte Pacheco Pereira qui fait imprimer Esmeralda de situ Orbis, écrit entre 1505/1508.
- 1523-1524, la première expédition du florentin Giovanni da Verrazzano et du français Antoine de Conflans, en Amérique du Nord, commanditée par le roi de France, François Ier, est à l’origine de la fondation de New York. Dans la liste des ouvrages nautiques d’Antoine de Conflans, il y a Le Grant Routtier de Pierre Garcie.
Les volvelles
La roue pôle-homme devient un instrument de marine pratique à partir du milieu du XVIe siècle, par la création de plusieurs volvelles articulées (roues pivotantes les unes sur les autres).
- 1524, Petrus Apianus publie Cosmographicus Liber. Dans la seconde édition (1530) du De Principiis Astronomiae & Cosmographiae de Gemma Frisius est apparue une figure de Pierre Apian : la volvelle. Cette dernière, associée à un cadran solaire, peut être utilisée comme horloge pour déterminer l’heure de la nuit. Le disque interne est configuré pour afficher la phase actuelle de la Lune à travers la fenêtre. Après avoir déterminé l’angle horaire de la Lune (avec un cadran solaire utilisé comme cadran lunaire et solaire) et ayant réglé le cadran lunaire de la volvelle sur cet angle horaire, on peut trouver l’emplacement du Soleil et déterminer l’heure de la nuit.
- 1526, Pedro Nunes publie l’Astronomici epitome sphœra, puis en 1527 le Traité de la sphère et études nautiques. Il présente la Roue polaire, qu’il appelle « astrolabii Nocturni ». Cet instrument permet de calculer l’heure durant la nuit avec la Polaris, sa position, les marées et l’âge de la Lune.
- 1538 - 1541, les trois Roteiros de João de Castro, Roteiro de Lisboa a Goa - Roteiro de Goa a Dio - Roteiro de Goa a Soez, terminent les travaux portugais dans la première moitié du XVIe siècle. Ses trois Roteiros traitent toutes les questions nautiques d’importance : les courants maritimes, la régularité des vents, la côte, les ports, les marées, instruments nautiques, les horloges, les éclipses et enfin la déviation de l’aiguille et le calcul des longitudes. Ils reprennent la logique éditoriale du Grant Routtier (1520) de Pierre Garcie dit Ferrande.

- 1545, Alphonse de Saintonge adapte l’œuvre de Martín Fernández de Enciso (1519) : La Cosmographie avec l’espère et régime du Soleil du nord par Jean Fonteneau dit Alfonse de Saintonge, capitaine-pilote de François Ier. Il reproduit les tables du Règlement d’Évora, calculées pour un cycle de 4 ans, et la déclinaison du Pôle.
- 1545, Pedro de Medina édite Arte de navegar en espagnol en 1545 puis en français en 1554.
- 1551, Martín Cortés de Albacar, cosmographe du roi d’Espagne, publie des tables plus simples de la déclinaison du Soleil dans son manuel pour marins : Breve Compendio de la sphera y de la Arte de navegar con nuevos instrumentos y reglas, exemplificado comn muy subtiles demonstraciones. Sevilha : casa de Anton Alvarez, 1551. Il est traduit en anglais en 1561 sous le titre de The arte of navigation.
- 1573, A Regiment of the Sea de William Bourne reprend les tables de Martin Cortés (1551) qu’il simplifie pour les mettre à la portée des navigateurs.
- 1670, Oronce Fine est un astronome français (1494-1555), ses travaux sont imprimés : Cosmographie avec la figure d’une roue pôle-homme.
XVIIIe siècle, le nocturlabe
Le nocturlabe sera la dernière étape de cette science pratique de la roue pôle-homme. Il sera remplacé par le sextant, lorsque l'appareil pourra être utilisé en regardant le soleil sans abîmer les yeux.
- 1745, la roue pôle-homme devient un instrument de construction plus complexe, avec deux volvelles pivotantes et une alidade. Elle sera connue comme nocturlábio de ponteiro ou nocturlabe[14]. Celui-ci se compose de deux volvelles concentriques. La première est un cadran des mois. La deuxième, mobile et munie d’un index, est un cadran des heures. La troisième partie est une alidade mobile. Cette alidade est dirigée sur l’étoile Kochab. Sa position permet de lire l’heure sur la deuxième volvelle, à n’importe quel moment de l’année. Au dos de l’instrument, on peut calculer l’établissement du port, à partir d’un cadran des âges de la Lune[15].
Utilisation
cadran des heures
La roue pôle-homme est un cadran des heures qui est étalonné en 24 heures par l’aiguille céleste : étoile polaire > Gardes (Kochab et Perkhab).
Pierre Garcie annonce un instrument nautique, en l’absence de sablier (horloge), quadrant et boussole (compas). Cette roue pôle-homme présente une roue de 24 secteurs, utilisée comme 24 quinzaines de jours pour la 1re couronne et 24 heures (2 fois 12 heures) pour la 2e couronne avec un corps humain au centre. Le sens est direct d’est en ouest (sens inverse des aiguilles d’une montre). En cas de destruction de cet appareil, le corps d’ un marin peut servir de repère mnémotechnique.
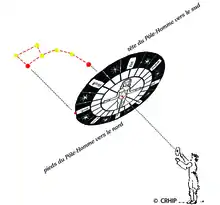
En Atlantique, un marin qui veut calculer l’heure la nuit du met la Roue Pôle-Homme face à soi, contrairement à une utilisation normale d’une rose des vents qui est placée horizontalement pour les mesures d’ angle. Du point de vue astronomique, et contrairement à une carte terrestre, on observe des objets situés au-dessus de vous et non en dessous : d’où le fait que l’est et l’ouest sont respectivement à gauche et à droite ; le haut est le sud et le bas est le nord.
Si on observe le ciel on constate que les étoiles tournent autour du Pôle, de la droite vers la gauche, quand on les observe, face au nord sous nos latitudes. Le Soleil et la Lune tournent, quant à eux, de la gauche vers la droite toujours dans l’hémisphère nord mais on les observe face au sud. Pourtant le mouvement apparent des astres étant dû à la rotation terrestre, les astres tournent d’ un même mouvement dans l’espace, c’est la position de l’observateur qui les fait paraître changer de sens. Il faudrait spécifier chaque fois la position de l’observateur : face au sud ou face au nord ; les explications deviennent alors pénibles. Pour y remédier, on prend pour repère cet homme de la roue pôle-homme, épinglé sur le Pôle Nord céleste et qui regarde donc toujours vers le sud et on parlera de la position d’ un astre en disant qu’ il est dans le bras droit ou bien dans le bras gauche.
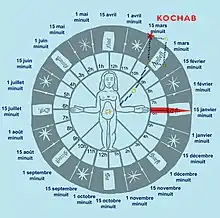
La Polaire étant au nombril du bonhomme, le méridien coupe l’horizon par les pieds au nord et dans le prolongement de la tête au sud. On sait désormais de quoi on parle d’une façon simple. s’agit donc d’ une simple convention de signe exactement comme on a inventé tribord et bâbord qui sont des directions repérées par rapport à l’avant du navire, alors que les mots de droite et gauche sont un repérage par rapport à l’observateur.
§ Exemple d'utilisation pour calculer l’heure nocturne du 15 février 1520
- 1re couronne, [mi-janvier] orientée vers EST ;
- étoile polaire au centre de la roue ;
- pointer Kochab sur le bord extérieur ;
- sur la 2e couronne, compter les heures entre la position/Kochab et la position/mi-janvier soit 4 heures ;
- sur la 1re couronne, positionner la date du et lire l’écart avec la position/mi-janvier, soit 2 heures ;
- faire la différence entre l’ heure relevée de Kochab et l’ heure de la date d’ observation, soit 4 - 2 = 2 heures ;
- Kochab est après la date de lecture du -minuit, d’où rajout à minuit ; il est 2 heures après minuit, au moment de l’ observation.
cadran aux étoiles
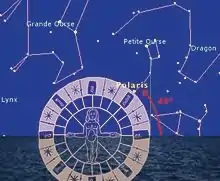
Pierre Garcie propose le calcul de la hauteur de l’étoile polaire, Polaris, et de sa déclinaison au pôle nord, avec la roue pôle-homme utilisée comme quadrant. De là, le marin peut définir la latitude du lieu d'observation. La 3e couronne au centre de 360° représente 8 vents, étalonnée par quart de 1 vent = 45° ; la 2e couronne de 24 quarts représente 360°, étalonnée par quart de 15° ; la 1re couronne de 32 quarts (dessin étoilé), représente 360°, étalonnée en quart de 11,25° (ou 11°15’).
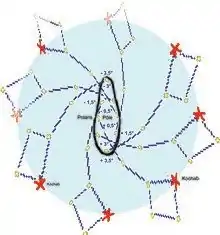
§ Exemple pratique pour calculer la hauteur de la Polaire d'un lieu déterminé
- tenir la roue devant soi, l’axe nord-sud dans l’axe du corps Tête/Pied ;
- orienter la roue de manière que la cardinale EST soit sur l’ horizontale ou ligne d’ eau ;
- trouver l’azimut de Polaris (référence A) sur le bord extérieur de la 1re couronne, en tendant + ou - le bras qui tient la roue ;
- compter le nombre de quarts de l’est à Polaris, soit ici : 4 quarts (pour un cadran de 32 aires) ou 3 quarts (pour un cadran de 24 heures) ;
- chaque quart valant 11,25° (360°, par 32 quarts, 1re couronne) ; ou 15° (360°, par 24 heures, 2e couronne), l’ exemple donne : 45° ;
- la mesure se fait à minuit et au moment du calcul de l’ heure, il est possible de relever la déclinaison de Polaris par rapport au pôle nord (+ ou - 3°), en positionnant cette étoile sur le bord du nombril. Cette valeur sera utilisée pour corriger la hauteur de la Polaire. Cette forme de nombril se rapproche de la forme que propose Ibn Majid : la lettre (arabe) lam : ل. Le marin applique la rectification en plaçant la Polaris sur le bord du nombril déformé et mesurer l'écart avec le bord de la Polaris en référence A ;
- la déclinaison donne +1°30', la latitude serait ainsi : 45°+1°30' = 46°30', soit la latitude au niveau du port des Sables-d'Olonne.
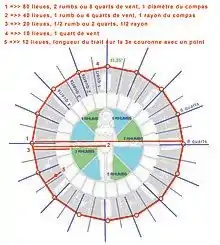
cadran compas
Un marin considère que le navire ne suit jamais la route qu’il est supposé suivre[3]. Les problèmes à résoudre au quotidien sont donc des problèmes de dérive. Pierre Garcie propose un Règlement des lieues et de la dérive à estimer. L’estime est une méthode de navigation où la position actuelle du navire est déduite en reportant la direction suivie et la distance parcourue à partir d’un point de départ parfaitement connu. C’est, à ce moment, une méthode graphique qui doit être reportée sur une carte marine ou portulan. La transcription graphique de la route est le cadre dans lequel s’inscrit le graphique de l’estime. Cela semble sûr, on part sur une route oblique Nord-Sud jusqu’à couper la parallèle du port d’arrivée et, de ce point, on continue sur une route Est-Ouest jusqu’au port d’ arrivée. Mais l’expérience montre que le navire pourra rarement suivre cette route tout du long ; des sautes de vent vont engendrer des parcours parasites qu’il faudra prendre en compte.
Il faut donc à la moindre altération forcée de la route être capable de tracer sur la route initiale le point où cet incident a lieu. Pour cela il suffit de connaître le nombre de milles parcourus depuis le départ et de les reporter sur la carte après les avoir transformés en distance sur la carte par le truchement de l’échelle portée en marge.
Le pilote trace sa route en utilisant les lignes entrecroisées (marteloire) du portulan inscrites à partir de rose des vents sur une carte portulan. Il trace ainsi une route surface à partir de la vitesse estimée et du temps passé, et en conséquence, indique la distance parcourue. Puis il applique une première correction qui concerne la dérive estimée due au courant et une deuxième correction qui concerne la dérive due au vent. On obtient alors le cap vrai, qui est l’ angle avec le nord que l’ on doit suivre au compas pour courir sur la route fond. En utilisant la méthode de calcul par la fin, le pilote estimait le point où il était.
Cette estimation était source d’erreurs accumulées, à la suite de plusieurs jours de route. Un degré en erreur plus ou moins pouvait représenter 20 lieues ou 110 km d’ écart avec le point recherché.
§ Exemple pour calculer la dérive
Pierre Garcie décrit une roue pôle-homme, utilisable comme compas, constitué de 8 rumbs de vent ou 32 quarts de vent. La figure représente les huit directions premières [N - NO - O - SO - S - SE - E - NE] avec huit étoiles intercalées pour les directions secondaires [NNO - ONO - OSO - SSO - SSE - ESE - ENE - NNE]. Le marin a ainsi un cadran compas de 16 directions représentées (chacune de 1/2 rumb ou 2 quarts) et 16 autres directions imaginaires. Ce compas permet d’ exprimer le cap suivi par le navire avec 32 quarts de vent, et par équivalence avec deux fois 12 heures ou huit fois 45°.
Cet ensemble permet d’ évaluer succinctement la dérive d’ un bateau en fonction de sa route, des courants et du vent. Voici un extrait du Règlement des Lieues : « (...) Exemple familier : si tu veux naviguer sur une route qui vise le nord et le sud comme [de La Rochelle à Santander] et que tu prennes un quart de nord-est ou de sud-ouest ou de nord-ouest ou de sud-est, ce quart de vent te déportera [de] 16 lieues en 80 lieues. Sache qu’ en 80 lieues, un demi-rhumb de vent qui fait 2 quarts de vent porte un navire 32 lieues au nord ou au sud. » Le Grant Routtier, f° 7r (p. 13)[2]
Cela signifie que si vous faites 80 lieues à un cap différent de 2 quarts de vent de votre route désirée, vous serez écarté de 32 lieues de votre point désiré. C'est le résultat de la formule : Écart = Longueur parcourue x Sinus de 11°1/4. Cette question était résolue graphiquement, sans calcul, par le marteloire.
cadran lunaire - cadran des marées
Pierre Garcie décrit dans Le Grant Routtier un mode opératoire pour calculer l’âge de la Lune et celui des marées avec la roue pôle-homme. Chaque cadran (celui des dates, celui de l’âge de la Lune, celui des rhumbs et celui des marées) sont sur la même figure. Un marin qui veut calculer, en un lieu donné, l’âge de la Lune et le déroulement des marées, doit d’ abord connaître le nombre d’ or de l’année d’ observation, puis l’épacte. Une fois défini le Nombre d’or et l’épacte calculés, le marin établit la Nouvelle Lune du début de l’ année solaire en mars de l’année considérée (année médiévale). Il est alors possible d’ utiliser la roue pôle-homme pour calculer l’âge des marées, définissant ainsi l’établissement du port, ou le cycle des marées de ce port à un moment donné[16].
En astronome et marin pédagogue, Pierre Garcie décrit quatre étapes pour utiliser la roue pôle-homme. Étape 1 : calculer le Nombre d’or de l’année en cours et détermination de l’épacte ; Étape 2 : calculer la Nouvelle Lune (et Pleine Lune) en mars (début de l’année médiévale) [ou Étape 1 et 2 : Pierre Garcie donne une autre possibilité par la liste des dates du jour de Pâques, dimanche qui suit la Pleine Lune après l’équinoxe de printemps, le 21 mars] ; Étape 3 : lire l’établissement du port, lieu où le pilote veut arriver, dans le chapitre de la zone décrite par Le Grant Routtier[2]. Pointer sur la roue pôle-homme cet azimut ou direction, soit A (figure 5) ; Étape 4 : calculer l’ écart entre le 15e jour de lunaison (cadran date), soit B (figure 5), et l’établissement du port, soit A, ce qui donne un nombre de rhumb, soit C (figure 5) [ou Étape 4 : Pierre Garcie donne deux possibilités de calcul, soit par le cadran heure, soit par le cadran jour (« qui veut compter la Lune par les heures, puis par les jours »)]. La roue pôle-homme est prête. Étape 5 : pour calculer l’heure de la pleine mer un jour défini de l’année, il propose de pointer l’âge de la Lune sur la roue et d’ajouter l’écart C déjà défini précédemment.
§ Exemple de calcul de l'établissement du port
Pierre Garcie propose cinq étapes pour utiliser la roue pôle-homme. Ci-après, en exemple, le calcul de l’ heure de la pleine mer du , aux Îles Anglo-Normandes.
Étape 1 : Règlement de la Lune, suivant Le Grant Routtier (1520) : calcul du Nombre d’ or de l’ année 1520. Ce nombre et celui de l’ Épacte étaient donnés le dimanche par le prêtre lors de son prêche. Pierre Garcie explique comment les calculer, lorsqu’ il est en mer : division de 1520 par 19 et ne retenir que le RESTE de la division. Cela s’ écrit [1520%19] ou [1520 modulo 19] donne un RESTE = 0. À ce résultat, ajouter + 1. Nous sommes en calendrier julien.
Le Nombre d’ or est 1, il correspond à la première année du cycle de 19 ans.
Étape 2 : Calculer l’Épacte pour connaître la Nouvelle Lune (et Pleine Lune) en mars (début de l’ année médiévale) : l’épacte, ou concurrence, est le nombre de jours que l’année civile du Soleil surpasse celle de la Lune ou bien c’est l’âge qu’avait la Lune le dernier jour de l’année qui précède celle qu’on demande. Chaque année, la lune prend un retard sur le soleil de 11 jours. Ce nombre de l’épacte dépend du Nombre d’Or. Pierre Garcie propose ce calcul avec les doigts et mentalement. Son année médiévale commence le , lendemain de l’ équinoxe de printemps. Calcul : A — le Nombre d’Or est 1. B — compter ce nombre sur les trois doigts, soit 1 fois qui aboutit au premier doigt. Ce 1er doigt a un montant de 18. C — assembler le chiffre 1 (doigt) et 18, soit 1 + 18 = 19. D — Pierre Garcie poursuit en tout 3 fois ce calcul ; soit Nombre d’Or 1 sur le 2e doigt (montant 28) qui donne 29 ; enfin Nombre d’ Or 1 sur le 3e doigt (montant 38) qui donne 39. E — assembler le résultat : 19 + 29 + 39 = 87. F — ôter 3 fois 30 (durée d’une lunaison) = 90 de 87 (en E). G — il reste - 3.
L’épacte est – 3. L’année médiévale commence le . La Nouvelle Lune est 3 jours auparavant (19-20-21), soit le ; la pleine mer du est à 6 h solaire.
Étape 3 : Établissement du port au mois de , avec Le Grant Routtier : pour connaître le mouvement de la marée au voisinage d’un port particulier, Pierre Garcie donne des tables qui indiquent l’heure de la pleine mer au méridien du jour de la Nouvelle Lune dans un lieu donné. Nous trouvons ces tables d’établissement du port pour la zone Manche nord et ouest France, Manche sud Angleterre et nord Espagne, dans Le Grant Routtier. La situation du port est l’heure de la haute mer du matin le jour de la nouvelle Lune (âge = 0). « À Chausey, Guernesey, Jersey, Sercq et Herm, la Lune [est] au sud basse mer, à terre,et à l’ouest, [à] plaine mer[2] ».
Cela signifie qu’au premier jour de la lunaison, à la Nouvelle Lune du , aux Îles Anglo-Normandes, la pleine mer est « ouest », ou 6 heures du matin. Comme c’est le premier jour de la lunaison, par définition le Soleil passe en même temps que la Lune au méridien, il est donc 6 heures du matin au Soleil. La pleine mer du soir sera donc 12 heures après, à 18 heures ou 6 heures de l’après-midi.
Étape 4 : calculer l’âge de la lune et de la marée du aux Îles Anglo-Normandes, avec la Roue Pôle-Homme : Pierre Garcie a besoin de : A — un cadran de lunaison de 30 jours qu’il réduit à une demi-lunaison de 15 jours (cercle bleu) sur 360°. B — un cadran compas de 32 rumbs qu’il réduit à 16 quarts ou rumbs (cercle blanc) sur 360°. C — un cadran de marées de 24 heures (cercle vert) sur 360°. D — un cadran annuel des marées, réduit à une demi-année de 360 h (cadran bleu) sur 360°.
- Roue pôle-homme et établissement du port
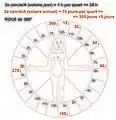 cadran solaire annuel © dessin CRHIP
cadran solaire annuel © dessin CRHIP cadran annuel des marées
cadran annuel des marées cadran lunaire annuel
cadran lunaire annuel cadran journalier des marées
cadran journalier des marées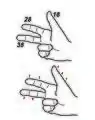 méthode de calcul sur les doigts © dessin CRHIP
méthode de calcul sur les doigts © dessin CRHIP
Étape 5 : poursuite du calcul : E — rappel des données acquises pour 1520, le Nombre d‘Or est 1 ; l’épacte est -3 ; la Nouvelle Lune de mars est le , soit un doigt en B sur la roue pôle-homme. La pleine mer est à 6 h aux Îles anglo-normandes. F — méthode utilisée, 3 [NO 1 + mars + 1er] + 4 (d’avril à juillet) + 1 (1er août) = 8. L’année finissant le , au mois d’août, la date de départ est le . La Nouvelle Lune est 8 jours avant, soit le . La pleine mer est à midi ou minuit. G — la situation du port des Îles Anglo-Normandes, le est 6 h : soit un doigt A posé sur le cadran compas à 6 h ou ouest ou 4 quarts. H — Le , dont l’ âge de la Lune est 7 jours [20-13 août], est à positionner par le cadran lunaison blanc : soit un doigt C posé sur S1/4SO ou 174 h (7 jours x 24 h + 6 h) ou entre 7 et 8 quarts. I — Lire sur le cadran vert des marées, l’heure de pleine mer, soit +/- 11 h 30’.
Par un calcul moderne, elle est définie le à 10 h 46’. La précision relative est suffisante pour arriver en sécurité une à deux heures avant et après sur ce lieu.
Références
- Bensaúde, Joaquim. L’astronomie nautique au Portugal à l ’ époque des grandes découvertes, 1912.
- Bernard de Maisonneuve, Pierre Garcie dit Ferrande ; le routier de la mer, v-1490, 1502, 1520, CRHIP, 2015 (ISBN 978-2-7466-8417-1) Prix de l'Académie de marine, 2016
- Com’ Nougué, Michel. Les Nouvelles Méthodes de Navigation durant le Moyen Âge, Conservatoire national des arts et métiers - CNAM, 2012.
- Amiral François Bellec, Histoire universelle de la navigation, Volume 1, Les découvreurs d'étoiles - J.P de Monza, 2016
- Dutarte, Philippe. Les instruments de l ’ astronomie ancienne de l ’ Antiquité à la Renaissance, Paris, Vuibert, 2006.
- Vaticanus lat. 644 fol. 76r
- bibliothèque Marciana de Venise (Ms lat. VIII.22 fol.1r)
- « Bibliothèque d'Avranches »
- École des interprètes de Tolède, sous la forme de binômes (moine chrétien-lettré arabe), unissant deux spécialistes d’une même matière : un lettré arabisant traduit les textes de l’arabe vers le vernaculaire. Juan Vernet et Julio Samso, Les développements de la science arabe en Andalousie in Roshdi Rashed (éd.), Histoire des sciences arabes. T.1. Astronomie, théorique et appliquée. Paris, Seuil, 1997, p. 285 à 287.
- Guy Beaujouan et Emmanuel Poulle, Les origines de la navigation astronomique du XIVe au XVe siècle in Le navire et l’économie maritime du Moyen Âge au XVIIIe siècle principalement en Méditerranée. SEVPEN, Paris, 1957.
- Deux siècles avant le Christ, l’étoile polaire se trouvait environ à 12° du Pôle. Cette étoile se rapproche du Pôle de plus en plus jusqu’à l’an 2095. Elle arrivera alors à 26’ d’écartement ; ensuite elle commencera à s’en éloigner.
- « Navigation Portugaise »
- Regimento de Munique et Regimento de Evora (Guía Náutico)
- « nocturlabe »
- Bernard et Mireille de Maisonneuve, Le Maidstone, miroir d'une mémoire, Arhims, 1992. (ISBN 978-2-9500688-2-8)
- Com ’ Nougué, Michel. Le calcul des marées au Moyen Âge, Chronique d ’ Histoire Maritime – SFHM, n°78, juin 2015.
Voir aussi
Bibliographie
 : document utilisé comme source pour la rédaction de cet article.
: document utilisé comme source pour la rédaction de cet article.
Bensaúde Joaquim, ingénieur et historien portugais, a apporté une contribution remarquable à l’histoire des grandes découvertes maritimes portugaises et en particulier sur le Règlement de l’astrolabe, appelé aussi Règlement de Munich [1509] et Règlement d’Évora [1516]. Dans cette synthèse est utilisé son ouvrage : L’astronomie nautique au Portugal à l’époque des grandes découvertes. [1912].- Beaujouan Guy, Poulle Emmanuel, Les origines de la navigation astronomique du xive au xve siècle, in Le navire et l’économie maritime du Moyen Âge du XVe au XVIIIe principalement en Méditerranée ; Travaux du 1er colloque international d’histoire maritime, 1956 - Paris, SEVPEN. [1960].
- Amiral François Bellec, Histoire universelle de la navigation, Volume 1, Les découvreurs d'étoiles - J.P de Monza, 2016.
- Com ’ Nougué Michel, ingénieur et historien français, a contribué à l’apport de la science nautique arabe avant l’essor des Portugais. Doctorat CNAM : Les Nouvelles Méthodes de Navigation durant le Moyen Âge. [2012].
- Com ’ Nougué, Michel. Le calcul des marées au Moyen Âge, Chronique d’Histoire Maritime – SFHM, no 78, .
- Dutarte, Philippe. Les instruments de l ’ astronomie ancienne de l ’ Antiquité à la Renaissance, Paris, Vuibert, 2006.
- Maisonneuve Bernard de, Pierre Garcie dit Ferrande - le routier de la mer, v.1490 - 1502 - 1520, CRHIP, 2015.
- Texeira da Mota Avelino, L’art de naviguer en Méditerranée du XIIIe au XVIIe siècle et la création de la navigation astronomique, in Le navire et l’ économie maritime du Moyen Âge au XVIIIe siècle principalement en Méditerranée ; Travaux du 2e colloque international d’histoire maritime, 1957 - Paris, SEVPEN. [1958].