Quadrant horaire
Les quadrants horaires sont des cadrans solaires de hauteur anciens, portables et de la famille des quadrants.
La hauteur du Soleil étant prise, ils permettent, à l'aide d'un fil à plomb et d'un pointeur, de lire l'heure sur le corps de l'instrument où est tracé un réseau de lignes horaires.
Au préalable à la lecture de l'heure, il convient d'effectuer quelques réglages simples en fonction du type de quadrant utilisé et de la date de l'observation.

Ils sont connus en Occident depuis le Moyen Âge, mais leur origine se trouve assurément dans les pays arabo-musulmans (une mention en ayant été trouvée dans un manuscrit égyptien daté probablement du IXe siècle ou Xe siècle).
Approche élémentaire
Description
L'instrument est composé de quelques éléments de base que l'on retrouve sur pratiquement tous les quadrants horaires. Ce sont :
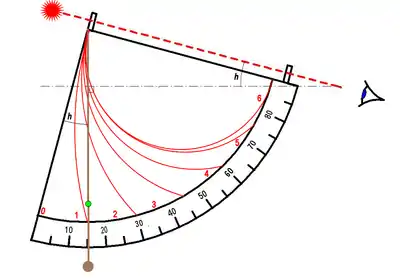
- le corps du quadrant, ayant la forme générale d'un quart de cercle, sur lequel on trouve un secteur gradué de 90° vers son bord extérieur : le limbe ;
- le système de visée comprenant deux pinnules à œilleton fixées sur un côté du quadrant ;
- un fil à plomb qui permet de vérifier la verticalité de l'instrument lors de la visée du Soleil (qui ne doit pas être regardé en face) et qui indique sur le limbe la hauteur de l'astre du jour ;
- un réseau d'heures tracé sur le corps du cadran. Ce réseau, qui dépend de la méthode de construction choisie, est de forme variable et les heures, suivant l'époque, peuvent être des heures temporaires et/ou des heures équinoxiales ;
- une petite perle-index, ajustée « glissant serré » sur le fil à plomb, après un réglage adéquat, indiquera, lors de la visée du Soleil, l'heure d'observation sur le réseau horaire[1].
Sur la figure ci-contre le réseau horaire (en rouge) représente les six heures temporaires du matin, l'heure de midi étant la sixième heure ; les heures de l'après-midi se superposent par symétrie sur les heures du matin, soit par exemple les couples 5-7, 3-9, 1-11. La perle coulissante (en vert) indique que l'on est au début de la deuxième heure du matin ou un peu avant la onzième heure de l'après-midi.
Réglage
La hauteur du Soleil varie en fonction de la latitude, de la déclinaison solaire et de l'heure de l'observation.
La formule suivante donne cette hauteur :

où h est la hauteur angulaire du Soleil, φ la latitude du lieu, δ la déclinaison du Soleil et H l'angle horaire du Soleil (H vaut 0° à midi et par exemple 15° à 13 h…).
La hauteur du Soleil à midi où H = 0° est donnée par :
Le réglage de la perle s'effectue sur la ligne horaire de midi en tenant compte de la latitude du lieu d'observation et de la déclinaison solaire[N 1].
Pour une latitude de 47° et pour une déclinaison actuelle de 23°26', arrondie à 23,5°, qui correspond à la date du solstice d'été vers le [N 2], on procédera au réglage de la façon suivante :
- déterminer la hauteur méridienne du Soleil à la date considérée, d'après l'expression (2) : hm = 90 - 47 + 23,5 = 66,5° ;
- tendre le fil sur la graduation 66,5° ;
- amener la perle sur le demi-cercle de la 6e heure[2].
Lecture de l'heure
Après réglage, il suffit de viser le Soleil avec le quadrant.
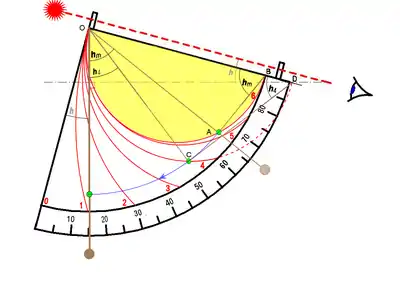
Le fil à plomb, vertical, indique sur le limbe la hauteur du Soleil et la perle donne l'heure (ici temporaire), soit h = 15,5° relevée un peu après la première heure du matin ou un peu avant la onzième heure de l'après-midi.
On peut remarquer que le lieu de la perle lors du déplacement journalier du fil à plomb est un arc de cercle centré en O et que son rayon correspond à sin h que l'on retrouve dans (1) expression de la hauteur du Soleil.
Ainsi, sur la figure, où tous les demi-cercles horaires sont centrés sur la droite OD, on aura :
- pour la sixième heure, si l'on considère le triangle rectangle OAB inscrit dans le demi-cercle de diamètre OB pris égal à 1 on a : l'angle OBA = hm comme angles à côtés perpendiculaires et OA = sin hm ;
- pour la quatrième heure, dans le triangle OCD, on aura l'angle ODC = h4 et OC = sin h4.
Quelle que soit l'heure considérée, la valeur sin h caractérise le lieu de déplacement de la perle[3].
Cette propriété se retrouvera sur tous les types de quadrants présentés.
Typologie
Les quadrants horaires sont d'origine arabe, mais les sources manuscrites sont rares et elles ont été publiées tardivement. Les quadrants arabes ne seront abordés ici qu'après étude des différents types d'instruments connus en Occident.
Les plus anciennes mentions occidentales des cadrans horaires datent du Moyen Âge central qui s'étend du XIe aux XIIe et XIIIe siècles. Ils sont assez bien documentés mais leur désignation était assez floue du fait de l'absence de règles typologiques.
Ce n'est qu'en 1981 qu'Emmanuel Poulle propose une classification en prenant en compte les définitions d'usage des instruments. Cette typologie se veut chronologique. Dans l'ordre d'apparition en Occident on trouve alors[4] :
- le quadrant sinus ou quadrans vetustissimus - superlatif latin du quadrant suivant, le quadrans vetus. C'est certainement le premier quadrant introduit en Occident à la fin du Xe siècle. Il comprend un réseau de lignes parallèles à définition trigonométrique. Ce n'est donc pas un quadrant horaire. Il ne sera pas abordé ici ;
- le quadrant ancien ou quadrans vetus, connu depuis le XIIe siècle. C'est la première famille de quadrants horaires caractérisés à l'origine par un diagramme d'heures temporaires se présentant sous forme d'arcs de cercles (comme sur les figures précédentes). Certains quadrants seront adaptés à une seule latitude, d'autres dits universels seront utilisables sous différentes latitudes grâce à un curseur-calendrier facilitant le réglage. Plus tard le quadrant ancien inspirera le tracé de quadrants à heures égales ;
- le quadrant nouveau ou quadrans novus[N 3], dit aussi astrolabe-quadrant, dont l'invention a longtemps été attribuée à Profacius en 1263. Ce n'est qu'un astrolabe planisphérique réduit par rabattements et rotation à un quart de cercle ; Certains de ces instruments comportent un diagramme d'heures temporaires, comme le quadrant ancien ;
- des quadrants à heures égales, apparaissent dès avant le XVe siècle. Ils sont liés à l'usage de l'horloge mécanique et à sa mise à l'heure. De construction simple, ils sont dédiés à une seule latitude et le réseau des heures équinoxiales est obtenu de différentes façons.
Récemment, en l'an 2000, l'étude d'un manuscrit conservé à la bibliothèque du Vatican fait apparaitre un nouveau quadrant daté du milieu du XIIe siècle[5]. Il va perturber l'ordre précédemment établi en prenant sa place avant le quadrans vetus. Il portera le nom de quadrans vetustior[N 4], nom proposé par E. Poulle entouré d'une équipe d'érudits spécialistes.
Les différents types de quadrants horaires seront présentés ici chronologiquement en tenant compte de ce dernier instrument.
Le quadrant vetustior
L'introduction en Occident de ce quadrant est supposée être antérieure au XIIe siècle : il est admis correspondre au quadra astrolabii mentionné par Hermann le Boiteux (1013-1054) dans son traité De utilitatibus astrolabii[6].
Quadrant théorique
Comme son nom quadra astrolabii l'indique, il est dérivé de l'astrolabe planisphérique ; c'est donc un instrument conçu pour une latitude unique. La latitude de 47°, comme celle de l'exemple du manuscrit du Vatican, sera choisie pour ce modèle théorique[7].
Il reprend le tracé des cercles astronomiques de l'astrolabe obtenus par projection stéréographique (équateur, tropiques, écliptique) et les place dans un quart de cercle par un double rabattement[N 5].
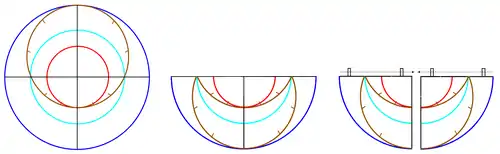
- la figure de base est la projection stéréographique des cercles astronomiques de l'astrolabe. Le cercle de l'équateur est de couleur émeraude, le tropique du Cancer (été) est en rouge, celui du Capricorne (hiver) en bleu et l'écliptique avec sa division zodiacale est en marron ;
- la deuxième vue montre le premier rabattement ;
- la troisième vue, correspondant au second rabattement, peut donner deux quarts de cercle, ou quadrants, suivant le sens (droit ou gauche) du rabattement.
Le modèle privilégie ici le quadrant avec rabattement à droite. Cette figure de base est construite à priori pour le milieu du XIIe siècle avec la latitude précitée de 47°, une inclinaison de l'écliptique « vraie » de 23°33' et une division angulaire zodiacale de base de 27,9°, 29,9°, 32,2° pour respectivement les signes du Bélier, Taureau et Gémeaux[N 6].
Après ce tracé préliminaire, sont mis en place les arcs de cercle de déclinaison solaire pour l'entrée et le milieu de chaque signe zodiacal.
Pour finir, les lignes horaires temporaires, numérotées de 1 à 6 (midi) pour les heures du matin et de 7 à 11 pour les heures de l’après-midi, sont tracées point à point à partir d'une table des hauteurs du Soleil.

Cette table est, elle aussi, construite à priori pour le milieu du XIIe siècle, avec la latitude précitée de 47°[N 7] - [8].
Tracé du quadrant
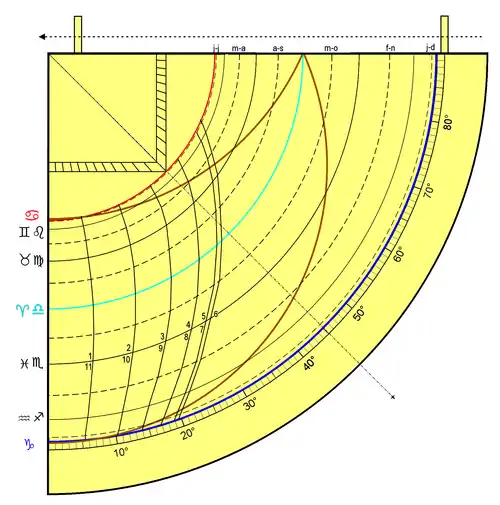
Quelques remarques :
- vers le milieu du XIIe siècle, le jour du printemps, correspondant à l'entrée du Soleil dans le signe du Bélier, se trouve être le 15 du mois de mars du calendrier julien employé à l'époque ;
- pour usage, le début des mois est donc admis être confondu avec le milieu de chaque signe zodiacal ; ce sera aussi l'hypothèse retenue dans l'exemple du manuscrit du Vatican ;
- le quadrant est agrémenté d’un carré des ombres - comme sur certains astrolabes - à usage topographique.
L'exemple du manuscrit du Vatican
Le quadrant du manuscrit Vaticano, BAV Ott. lat. 1631, commenté et illustré par Catherine Jacquemard, Olivier Desbordes et Alain Hairie, est du même type que le modèle théorique présenté précédemment. Par contre, le protocole de construction proposé est intéressant dans la mesure où il simplifie le tracé du quadrant en faisant abstraction de tout calcul astronomique[9].
- le tracé du double rabattement des cercles célestes est réalisé à partir d'une construction géométrique originale bien développée dans l'article présenté. Cette proposition implique une valeur de l'obliquité ε ≈ 23°35' donnée par les auteurs de l'article[N 8] ;
- l'emplacement du début des signes zodiacaux et des mois sur les arcs brisés de l'écliptique est proposé de 15° en 15°[N 9], ce qui est assez inexact ;
- suit le tracé des arcs des cercles de déclinaison du Soleil, centrés en O, qui s'appuient sur les points précédemment définis ;
- le tracé des lignes horaires est alors obtenu à partir d'une table des hauteurs du Soleil dont les valeurs sont données pour l'entrée et le milieu de chacun des signes du zodiaque[N 10]. Ces lignes horaires sont tracées point à point et reprises par les auteurs de l'article.
Un fil à plomb, apparemment sans perle-index permet la lecture, alors incommode, de l'heure.
Pour finir le quadrant est agrémenté d'un carré des ombres, dont la finalité est topographique.
Il est intéressant d'avoir une idée de l'erreur sur la lecture de l'heure due au tracé simplifié du quadrant du manuscrit du Vatican. Ceci pour sa finalité reconnue : donner l'heure vers 1150.
Une première solution consiste à superposer le quadrant du manuscrit avec son modèle théorique. Cette superposition est grossièrement correcte mais le quadrant du manuscrit n'étant pas publiable, l'illustration ne peut être donnée ici.
Par contre, l'examen de la table des hauteurs du Soleil donnée en annexe du manuscrit est exploitable dans ce sens.
Sa comparaison avec le modèle théorique - supposé exact -, en relevant les écarts entre les deux tables, permet de voir où se trouvent les erreurs les plus importantes[10].
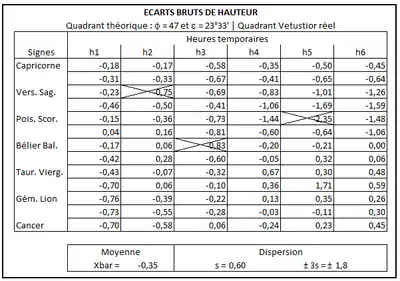
Dans cette table des écarts, après élimination de quelques valeurs aberrantes et analyse, on constate que la valeur moyenne des écarts de hauteur est de l'ordre de 0,35° et la dispersion, à 3 écarts-types, est inférieure à ±2°.
On peut alors en déduire les erreurs de temps brutes, pour chaque heure temporaire, dues aux hypothèses simplificatrices.
Sans entrer dans les détails, l'erreur la plus significative est due à l'emploi de la table des hauteurs établie pour une obliquité de 24° au lieu de 23°35' ; les autres simplifications n'ont guère d'influence au vu de la précision de l'instrument.
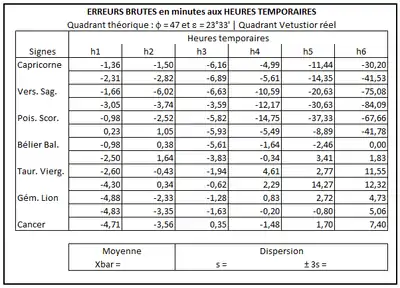
Globalement l'instrument donne l'heure avec une exactitude dont on pouvait se satisfaire à l'époque, à l'exception des valeurs relevées vers midi (h6) où l'erreur est très importante[N 11] - [11].
Le quadrant ancien ou quadrans vetus
D'origine arabe, il a vraisemblablement été introduit en Occident avant le XIIIe siècle. À partir de cette époque, Il est mentionné dans différents traités :
- le traité du quadrant de Sacrobosco mort en 1244 ou 1256 ;
- le traité du quadrant de maître Robert Anglès [Robert l'Anglais] à Montpellier, ca 1231-1276[12].
- un traité de Campanus de Novare (1220-1296) ;
- il fait l'objet du livre 9, le Libro del cuadrante, dans l'encyclopédie du savoir astronomique, le Libro del saber de astrología dit d'Alphonse X Le Sage, paru vers 1276.
Le quadrant ancien simple
Son approche élémentaire (description, réglage et lecture de l'heure) a servi d'exemple dans la première section de cette page.
Précisons ici le tracé des lignes horaires temporaires.
Diagramme des lignes horaires
Les lignes horaires ne sont pas tracées à partir des formules exactes (1) et (2) données plus haut. C'est une formule approximative qui est employée ; elle donne néanmoins de bons résultats pour des latitudes pas trop élevées. Elle permet de simplifier - mieux que pour le quadrant vetustior - le tracé des lignes horaires qui sont alors représentées simplement par des arcs de cercles.
- Construction géométrique

La partie utile du quadrant, recevant le diagramme des heures (temporaires) est le secteur de rayon .
Chaque ligne horaire passe par un premier point, le point et un second, situé sur l'arc , dont la position est donnée par l'arc , avec = 15°, = 30°, = 45°, = 60°, = 75° et = 90°[N 12].
Les centres des arcs de cercles , … des heures temporaires se trouvent respectivement sur la médiatrice des segments , … et sur l'axe .
- Formule mathématique
Chaque rayon de ligne horaire ( variant de 1 à 6) est donné par la formule suivante :
où est exprimé en degrés (de 15 en 15 pour variant de 1 à 6)[N 13] - [13].
- Erreur commise
Les lignes horaires n'étant pas tracées à partir des formules exactes, elles entrainent une erreur théorique sur la lecture de l'heure soulignée ici ; l'erreur est donnée en minutes d'heures temporaires.
| Latitude φ | Erreur max. |
|---|---|
| 30° | 6 min |
| 40° | 9 min |
| 50° | 14 min |
Utilisation du diagramme
L'intérêt du diagramme d'heures temporaires est qu'il est utilisable pour des latitudes quelconques pas trop élevées[N 14].
Guère employé sous sa forme simple comme instrument, il est néanmoins très utilisé au Moyen Âge islamique et occidental, dans les versions suivantes :
- tracé au dos de l'astrolabe planisphérique ;
- comme quadrant ancien simple dédié à une latitude donnée ;
- mais surtout, il servira de base au quadrant ancien universel ;
- il sera aussi tracé sur l'astrolabe-quadrant dit aussi quadrant nouveau.
Tracé au dos de l'astrolabe
C'est un tracé qui figure fréquemment au dos de l'astrolabe, sous sa forme simple et le plus souvent sous sa forme double plus fonctionnelle et esthétique. Ce diagramme permet de déterminer l'heure approximative temporaire pour une latitude quelconque ; c'est donc une avancée par rapport à l'astrolabe classique qui ne peut donner l'heure temporaire (exacte) qu'en utilisant les tympans l'accompagnant[15].
- Diagramme double d'heures temporaires
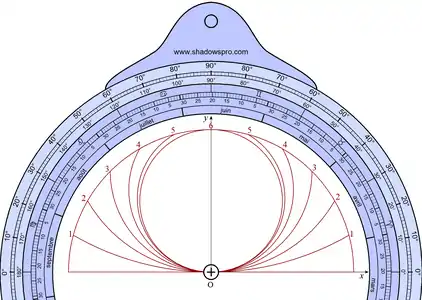 Localisation au dos d'un astrolabe.
Localisation au dos d'un astrolabe.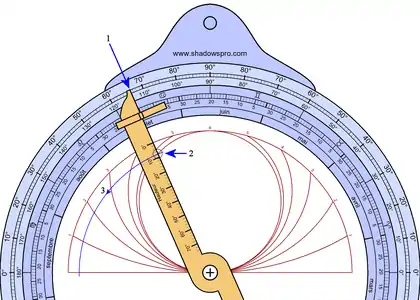 Utilisation avec l'alidade.
Utilisation avec l'alidade.
Soit à rechercher l'heure temporaire pour une latitude de 47° au jour du solstice d'été, comme vu précédemment :
- après avoir lu sur l'écliptique de l'araignée (sur la face avant de l'astrolabe) la déclinaison du Soleil à son entrée dans le signe du Cancer, 23,5°, déterminer la hauteur méridienne du Soleil à la date considérée, d'après (2) : hm = 90 - 47 + 23,5 = 66,5° ; au dos de l'instrument pointer avec l'alidade la hauteur 66,5° ;
- repérer l'intersection de l'alidade avec le demi-cercle de la sixième heure, la noter sur l'alidade (ici sur la graduation 9 de « hauteur[N 15] » ; l'heure du jour se trouve sur l'arc de cercle de rayon O9 ;
- faire pivoter l'alidade, pour l'amener en direction du Soleil. À cet instant lire l'heure au point 9 de « hauteur » de l'alidade. Par exemple, pour une hauteur de 27° il sera 2 heures temporaires du matin ou 10 heures temporaires de l'après-midi.
L'instrument « quadrant ancien simple »
Le quadrant est dédié à une latitude donnée :
On trouve sur l'instrument un calendrier zodiacal qui dispense de l'utilisation de tables de déclinaison du Soleil. Ce calendrier est construit dans un secteur circulaire, sur le pourtour du quadrant, en suivant les divisions angulaires de chaque signe zodiacal, données par la relation (2).
Pour la lecture de l'heure temporaire on procède comme précédemment en réglant d'abord le fil sur la date du jour et en amenant la perle sur le demi-cercle de la sixième heure, puis on vise le Soleil ; le fil à plomb donne l'angle de hauteur du Soleil et la perle indique alors l'heure temporaire.
Sur la figure on remarquera la colatitude 40°, correspondant à une latitude de 50°, et les angles de 16,5° et de 63,5° aux solstices donnés par la formule hm = 90 - 50 ± 23,5.
Il ne semble pas subsister d'exemplaires de ce type de quadrant. On trouve simplement sa description dans quelques ouvrages traitant du quadant ancien en général, tels Oronce Fine et Sebastian Münster.
Le quadrant ancien universel
Il s'agit d'un quadrant ancien utilisable sous n'importe quelle latitude, celle-ci étant donnée[16].
Il reprend le principe du quadrant ancien simple, décrit précédemment, en remarquant que le secteur circulaire qui reçoit le calendrier est constant dans ses dimensions angulaires, quelle que soit la latitude. Il suffit de déplacer le secteur pour le régler sur la colatitude adéquate.
Dans sa construction, le secteur circulaire mobile appelé curseur peut se déplacer dans une rainure semi-circulaire.
Réglé en position, il s'utilise comme le cadran ancien simple.
Le calendrier, zodiacal à l'origine, s'est vu adjoindre un calendrier civil pour en faciliter l'utilisation.
Le quadrant du Musée Galilée est pris comme exemple.
Commentaires : La chiffraison est de type gothique (fin XIVe siècle).
- la latitude est de l'ordre de 44,4° ; la colatitude correspondante est de 45,6°, elle permet le réglage du curseur en alignant l'entrée du signe du Bélier sur l'angle 45,6° du limbe[N 16] ;
- le jour de l'observation est supposé être le 1er mai, dans l'après-midi. Le fil à plomb est placé sur la graduation 62,6° correspondant à la date, la perle est glissée sur la sixième heure, heure de midi ;
- Pour finir, l'observation du Soleil donne sa hauteur h = 35° à un instant t où la perle indique l'heure : un peu avant le milieu de la dixième heure de l'après-midi.
- Premières représentations occidentales
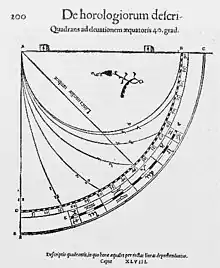
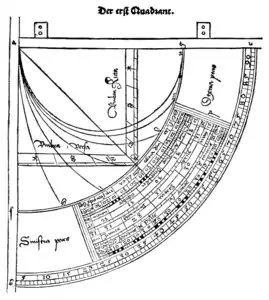 Quadrant de Sacrobosco, première moitié du XIIIe siècle, édition de 1534.
Quadrant de Sacrobosco, première moitié du XIIIe siècle, édition de 1534.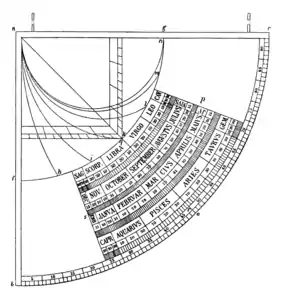 Quadrant de Robert Angles, ca 1231-1276, édition 1897.
Quadrant de Robert Angles, ca 1231-1276, édition 1897.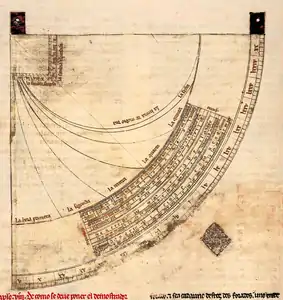 Quadrant du Libro del Saber, ca 1276.
Quadrant du Libro del Saber, ca 1276.
Des origines arabes
Les sources sont rares sur l'origine du Quadrans Vetus. En Occident, il n'existait, comme on a pu le voir, que des références latines médiévales et Castillanes.
C'est un article publié en 2002 par David A. King qui présente une source arabe probablement du IXe siècle ou au plus tard du Xe siècle. Il s'agit du Traité de Bagdad, conservé dans un manuscrit de la Bibliothèque nationale égyptienne au Caire[17]. David A. King suggère que ce traité anonyme soit dû à l'astronome Al-Khwârizmî.
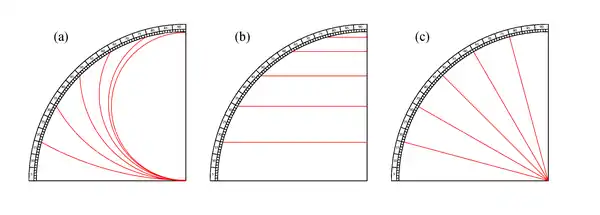
Il y est mentionné différents types de quadrants anciens universels donnés schématiquement ci-dessous. Les lignes horaires peuvent être représentées sous forme d'arcs de cercles (a), de lignes parallèles (b) ou de lignes rayonnantes (c).
Excepté pour le quadrant de type (a) décrit plus haut, l'usage des deux autres quadrants schématisés par King n'est guère explicite. King précise dans son article que l'astronome de Bagdad écrit simplement « l'usage de tous ceux-là [(b) et (c)] est le même »[18].
Le quadrant nouveau ou quadrans novus

Ce quadrant est une invention d'origine orientale qui a longtemps été attribuée à Profacius en 1263.
Ce n'est qu'un astrolabe planisphérique réduit par rabattements à un quart de cercle ; il est décrit sur la page astrolabe-quadrant. Comme l'indique R. D'Hollander « il nécessite une gymnastique intellectuelle particulière qui contraste avec la simplicité d'emploi de l'astrolabe planisphérique[19]. »
La détermination de l'heure inégale avec cet instrument admet différentes solutions :
- par des calculs trigonométriques facilités par l'instrument lui-même, à partir de la hauteur du Soleil ;
- par l'intermédiaire d'un diagramme d'heures inégales, comme décrit plus haut, qu'on trouve sur certains instruments ;
- en mesurant de nuit la hauteur d'une étoile[20].
Développons la détermination de l'heure en utilisant le diagramme des heures inégales, avec l'exemple suivant :
On doit pour cela calculer la hauteur méridienne du Soleil à la date donnée, d'après la formule (2) :
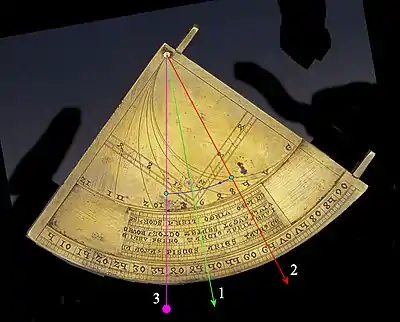
La déclinaison solaire est déterminée sur l'instrument (ici l'astrolabe-quadrant de Rouen tracé pour l'époque de Profacius) :
- au verso du quadrant, comme sur un astrolabe planisphérique, un calendrier civil et zodiacal indique que, le 1er mai, le Soleil est à 17° dans le signe du Taureau[N 17] ;
- sur l'échelle intérieure du limbe, repérer la place du Soleil dans le signe du Taureau (surligné en vert), ♉17° ; tendre le fil (de couleur fuchsia) sur ce point ; amener la perle sur le secteur « Taureau » de l'écliptique rabattue ; faire tourner ensuite le fil et sa perle (trajectoire fuchsia pointillée et fléchée) pour amener cette dernière sur l'échelle de déclinaison solaire, sur le côté du quadrant où est notée « l'échelle de 10 cm ».
Dans ces conditions :
Ce qui permet de déterminer l'heure suivant les étapes décrites plus haut. Au résultat final, pour h = 26° on trouve un peu plus de deux heures temporaires.
- Détermination de l'heure temporaire sur l'astrolabe-quadrant de Rouen
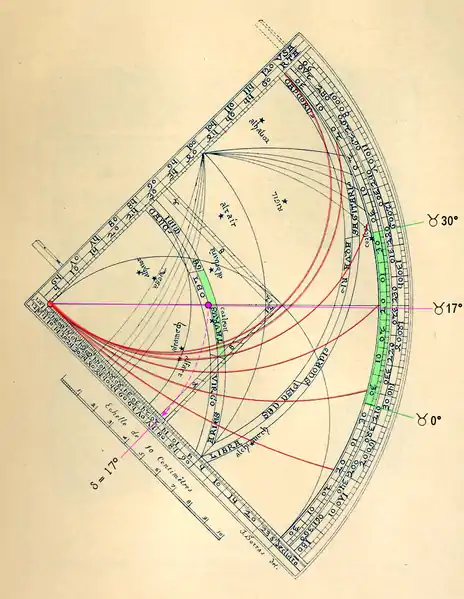 Recherche de la déclinaison solaire.
Recherche de la déclinaison solaire.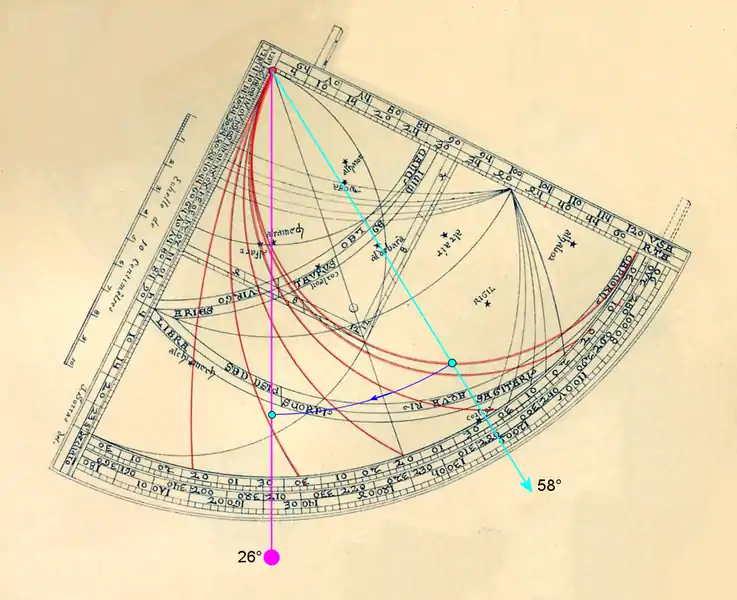 Réglages pour trouver l'heure.
Réglages pour trouver l'heure.
Les quadrants à heures égales
En Occident, au XIVe siècle, l'essor de l'horloge mécanique a probablement favorisé l'adaptation aux heures égales des instruments horaires de l'époque. Cette transformation a été nécessaire pour mettre à l'heure ce nouveau gardien du temps. Parmi ces instruments, dont certains étaient utilisés dès l'Antiquité, les quadrants dérivés du quadrant ancien occupent une place importante.
Ces nouveaux quadrants ne pourront être universels, la complexité et la confusion entre lignes horaires rendant cette représentation impossible. Ils seront alors tracés simplement pour une latitude donnée et différents modèles verront le jour au cours des siècles suivants.
Probablement en bois aux origines, les quelques exemplaires existants sont en laiton et dédiés à de riches personnalités.
Version de base
Il s'inspire du « quadrant ancien simple », mais le diagramme des heures, approximatif, est construit suivant un nouveau principe[21].

Du quadrant ancien simple sont conservés :
- d'une part, le secteur circulaire fixe dédié au calendrier zodiacal et tracé pour une latitude donnée. Sur la figure d'Oronce Fine, la latitude est de 48°40', soit une colatitude de 41,33° correspondant à l'entrée du Soleil dans le signe du Bélier ;
- d'autre part, le demi-cercle de la sixième heure inégale (heure de midi) qui devient la douzième heure égale.
Le diagramme des heures égales autres que l'heure de midi est construit à partir des lignes de déclinaison solaire des équinoxes (Aequinoxialis) et des solstices (Tropicus…), tracées sur le quadrant.
Une table des hauteurs du Soleil va permettre de définir sur les lignes de déclinaison précitées 3 points pour chaque heure. Ainsi, pour 10 heures du matin ou deux heures de l'après-midi on aura les 3 points suivants : 13°0' pour l'entrée dans le signe du Capricorne, 34°53' pour les équinoxes, 55°27' pour l'entrée dans le signe du Cancer.
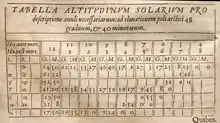
Ces 3 points étant reportés sur le quadrant, il sera tracé l'arc de cercle passant par ces trois points pour définir la ligne horaire correspondante.
Ce tracé est approximatif ; il va permettre néanmoins de définir un diagramme horaire simple. On pourra y adjoindre des lignes de déclinaison solaire supplémentaires qui par la suite permettront de se dispenser du secteur circulaire du calendrier zodiacal.
Quatre quadrants anglais, datés de la fin du XIVe siècle, semblent être les plus anciens quadrants de ce type conservés à ce jour. Il s'agit de quadrants tracés pour une latitude du sud de l'Angleterre et confectionnés pour le roi Richard II et son entourage.
- Quadrants dits de Richard II
 Quadrant de 1396, face d'usage (après consultation de la table du verso).
Quadrant de 1396, face d'usage (après consultation de la table du verso). Quadrant de 1396, face AR avec table de hauteurs méridiennes du Soleil.
Quadrant de 1396, face AR avec table de hauteurs méridiennes du Soleil. Quadrant de 1399 pour le roi d'Angleterre.
Quadrant de 1399 pour le roi d'Angleterre.
Ils sont datés respectivement de 1396 (marqué du signe du roi et mis en vente en 2011 par Bonhams), 1398 (Musée Dorset du comté de Dorchester), 1399[22] et ca 1400 (British Museum Londres)[N 19].
On peut souligner que, dans les dernières décennies du siècle, la cour de Richard II comme celle de Charles V pourraient bien avoir favorisé l'utilisation des heures égales ; un dossier administratif utilise les heures égales à l'occasion de l'abdication de Richard II, le [23].
Des versions supplémentaires de ce quadrant de base ont été proposées par différents auteurs aux siècles suivants :
Version mixte
Cette version propose sur un même quadrant un tracé des heures temporaires accompagné d'un tracé des heures égales.
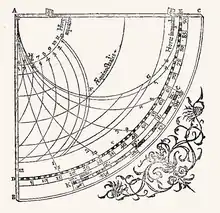
Pour éviter la confusion entre les lignes, le diagramme des heures égales est inversé : les quarts de cercle des « tropiques » sont intervertis.
Pour lire l'heure égale il faut alors régler la perle sur la date symétrique du calendrier zodiacal.
Version au tracé rectiligne
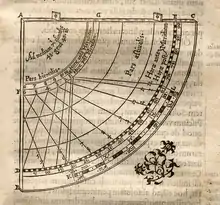
Les lignes d'heures égales sont rectilignes, le principe de tracé est alors différent de la version de base présentée plus haut.
- sur le quart de cercle FG on reporte, d'après des tables, les hauteurs du Soleil aux différentes heures des équinoxes ;
- sur le quart de cercle DE on reporte les hauteurs du Soleil aux différentes heures du solstice d'été ;
- tracer alors, pour chaque heure, les segments horaires qui sont dirigés vers la droite ;
- la lecture de l'heure, entre les équinoxes et solstice d'été, s'effectue en réglant la perle du fil à plomb sur le segment de 12 heures.
Les lignes horaires « d'hiver » sont tracées de la même façon ; elles sont dirigées vers la gauche.
Ces tracés sont approximatifs.
Ce type de quadrant a sa place sur le célèbre tableau Les Ambassadeurs d' Hans Holbein le jeune, peint en 1533.

Les quadrants tracés point à point
À la fin du Moyen Âge et au début de la Renaissance, le souci d'exactitude a peut-être favorisé l'émergence de diagrammes horaires obtenus directement à partir de tables de hauteurs du Soleil.

Ces tables, calculées ou construites et/ou vérifiées par l'expérience ont permis le tracé « exact » des lignes horaires.
Le report des valeurs de ces tables sur les quadrants s'est d'abord effectué point à point, puis les lignes horaires ont été représentées par des courbes lissées se rapprochant d'un modèle mathématique.
Une superposition de quelques lignes horaires tracées suivant le principe du quadrant « ancien » permet de constater les erreurs dues à ce dernier.
- Quadrants aux tracés mathématiques
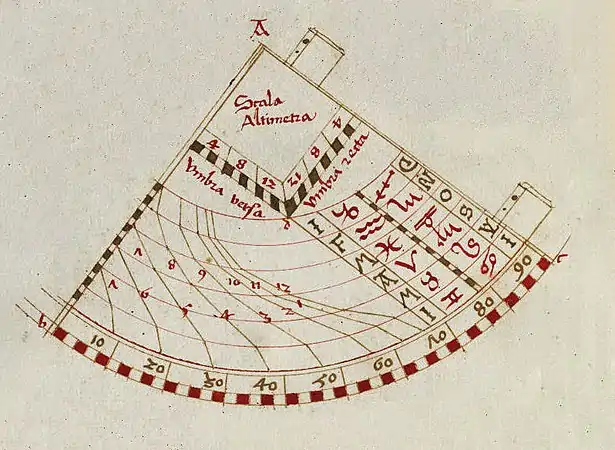 Quadrant à heures égales pour une latitude de 48°, construit point à point, esquisse manuscrite, vers 1500.
Quadrant à heures égales pour une latitude de 48°, construit point à point, esquisse manuscrite, vers 1500.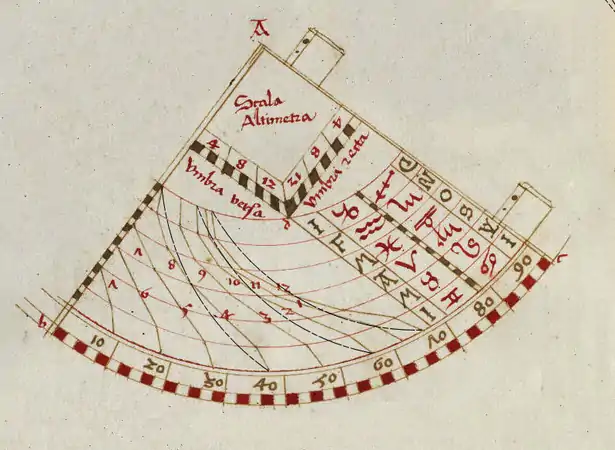 Comparaison du tracé point à point avec un tracé de type quadrant « ancien » (en trait mixte noir) pour les heures 8, 10, 12.
Comparaison du tracé point à point avec un tracé de type quadrant « ancien » (en trait mixte noir) pour les heures 8, 10, 12.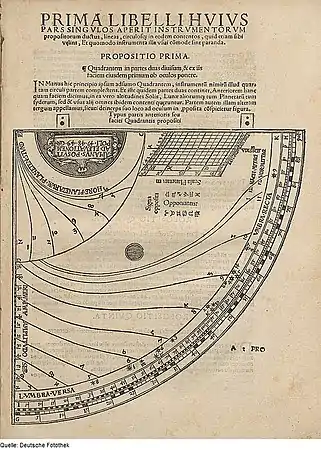 Quadrant aux tracés temporaire et équinoxial « exacts », Apian, 1532.
Quadrant aux tracés temporaire et équinoxial « exacts », Apian, 1532.
Le quadrant de Gunter

Ce quadrant, un peu particulier, a été conceptualisé par Edmund Gunter (1581-1626), mathématicien et astronome anglais[24].
En usage aux XVIIe et XVIIIe siècles, il en existe différents exemplaires disséminés dans les musées anglais.
Il est dit avoir été utilisé en navigation. Mais son exploitation n'est possible que pour une latitude donnée, celle du quadrant, ce qui ne peut que laisser dubitatif sur son emploi en mer.
C'est un instrument, dérivé de l'astrolabe, sur lequel on trouve en projection stéréographique - comme sur le quadrant vetustior et le quadrant nouveau - l'équateur (de couleur émeraude sur la figure), le tropique du Capricorne (en bleu), l'écliptique (en marron) et l'horizon du lieu, non représenté ici. La partie située au-dessus de l'équateur n'apparait plus dans la construction du quadrant.

Pour le reste il s'apparente plutôt au quadrant « ancien » à heures égales. On y trouve en effet le secteur circulaire fixe dédié au calendrier civil ainsi qu'un diagramme des heures équinoxiales sur la partie gauche en position d'utilisation. Ce diagramme est composé de deux réseaux d'heures : heures d'été dirigées vers l'intérieur du quadrant (sur la droite) et heures d'hiver dirigées vers l'extérieur (sur la gauche) ; ces réseaux sont construits point à point, en suivant le principe de disposition du quadrant au tracé rectiligne.
La partie droite est réservée à un diagramme des azimuts.
Ce quadrant a pu être agrémenté d'un carré des ombres ou d'autres compléments en fonction de l'usage escompté (tableau d'étoiles notamment).
D'après l'ouvrage de Gunter de 1623, De Sectore et Radio[25], le quadrant permet de trouver :
- le jour du mois ;
- l'heure du jour ;
- l'heure du lever et du coucher du Soleil, donc la durée du jour ;
- l'heure de nuit par les étoiles ;
- [l'azimut du Soleil]…

On peut remarquer sur la figure, sur le côté gauche, l'échelle de déclinaison solaire graduée de 0 à 23,5° ; au-dessus du limbe, le secteur calendaire civil où on peut deviner la colatitude de 37° ; la projection de l'horizon est chiffrée de 10 à 30 et l'écliptique est graduée de 10 à 90 ; au centre du quadrant, sur la gauche le diagramme des heures égales numérotées de 6 à 11 pour les heures d'hiver (sur l'équateur) et de 8 à 12 pour les heures d'été (sur le tropique du Capricorne).
Sur la partie droite on trouve le diagramme des azimuts numérotés de 20 à 120.
Un applet permet d'avancer pas à pas dans l'usage du quadrant[26].
D'autres sites présentent des quadrants de diverses collections[27].
Les quadrants ottomans

Ces quadrants ont été très en vogue dans l'empire ottoman, notamment à partir du XVIIe siècle jusqu'au début du XXe siècle.
Ils reprennent les grands principes de construction du quadrant vetustior ou du quadrant nouveau dit aussi astrolabe-quadrant décrits précédemment.
Leur fonction essentielle est la détermination des heures des prières islamiques pour une latitude donnée : la face astrolabique est dédiée aux différentes mesures, l'autre est à usage trigonométrique.
À l'examen, les quadrants ottomans se différencient des astrolabes-quadrants par une grande encoche sur le côté qui remplace les pinnules de visée ; la ligne de visée vers le Soleil est ajustée quand l'ombre du talon supérieur recouvre le talon inférieur.
De belle facture, ils sont généralement en bois verni avec de nombreuses décorations[28].
Description
La construction de ce type de quadrant résulte du tracé des cercles astronomiques de l'astrolabe obtenus par projection stéréographique et placés dans le quart supérieur gauche par un double rabattement.
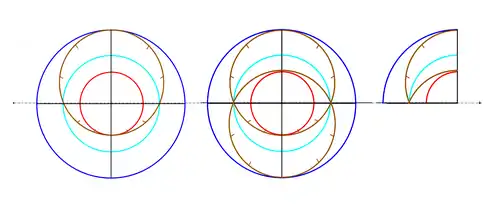
Le cercle de l'équateur est de couleur émeraude, le tropique du Cancer (été) est en rouge, celui du Capricorne (hiver) en bleu et l'écliptique avec sa division zodiacale est en marron.
Un dessin simplifié et chiffré à l'« occidental » d'un quadrant construit pour une latitude de 42° (colatitude 48°) met en évidence ces premiers éléments.
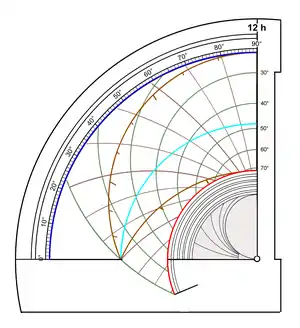
Sur ce quadrant on trouve en plus :
- d'une part, le réseau des arcs de cercles d'égale hauteur ou almucantarats tracés en vert. L'almucantarat 0° (hauteur = 0°) qui correspond à l'horizon du lieu d'observation, en gras, limite la zone d'exploitation du quadrant.
- d'autre part, le réseau des arcs d'azimuts du secteur correspondant est tracé en trait fin de couleur marron.
Ces deux derniers éléments, almucantarats et azimuts, permettent aussi de reconnaitre un quadrant ottoman et de le différencier de l'astrolabe-quadrant dit « quadrant nouveau ».
Le limbe reçoit vers l'intérieur une échelle graduée en degrés et, vers l'extérieur une échelle des cotangentes (non graduée ici) pour déterminer des longueurs d'ombre.
Le méridien (ligne de 12 h) reçoit les graduations des hauteurs solaires à midi.
La partie fonctionnelle de l'instrument se limite vers le centre (pôle) du quadrant à l'arc de cercle du tropique du Cancer. Dans cette zone centrale on trouve éventuellement un diagramme des heures temporaires (quadrant ancien simple ombré), puis différentes échelles graduées non détaillées ici[29].
Heures des prières
Les règles coraniques sont très vagues sur les instants où doivent être effectuées les prières.
À l'époque de l'usage des quadrants ottomans, par convention, le jour musulman qui se divise en 24 heures égales, commence au coucher du Soleil ; les heures de midi, du lever et du coucher du Soleil, « heures sataniques », sont interdites à la prière[30].
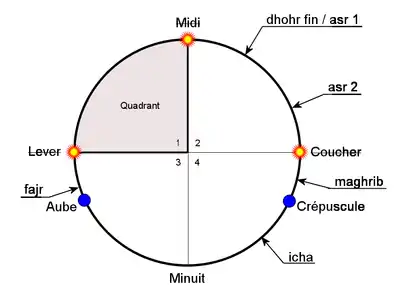
Les cinq prières traditionnelles de l'Islam, en suivant ces conventions, étaient dans l'ordre :
- Maghrib (prière du coucher) : prière qui commence après le coucher du soleil et se termine au crépuscule ;
- Icha (prière de la nuit) : prière qui commence quand la nuit tombe et que le crépuscule du soir disparaît ;
- Fajr (prière de l'aube) : prière qui commence à l’aube ou au crépuscule du matin ;
- Dhohr (prière de la mi-journée) : prière qui commence à la mi-journée, quand les rayons du soleil ont dépassé le méridien ; le dhor se termine au début du Asr (Asr1).
- Asr (prière de l’après-midi) : son horaire dépend de la grandeur de l'ombre d'un gnomon de référence. Plusieurs écoles s'affrontent pour en déterminer les instants de début et de fin. Sur les quadrants ottomans, il semble que les tracés de Asr soient conformes aux règles édictées par al-Biruni au IXe siècle dans son Traité exhaustif des ombres.

Tracé
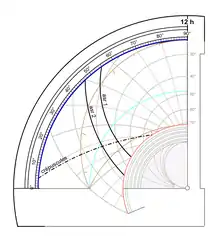
Le tracé de l'asr est supposé suivre les règles de Biruni. Asr 1 et Asr 2 sont deux courbes sensiblement parallèles. Elles proviennent du rabattement des courbes originelles du secteur 2 sur le secteur 1 du quadrant.
Le tracé des autres prières n'est pas représenté ici par manque d'informations. Il faut noter que ces dernières prières ne peuvent être obtenues à partir de la visée du Soleil puisqu'elles ont lieu quand ce dernier est sous l'horizon. Leur tracé sur les quadrants ottomans ne servait qu'à déterminer les instants où elles devaient être récitées.
À la place de ces tracés on trouvera celui des crépuscules astronomiques du matin (aube) et du soir qui interviennent dans la position respective des différentes prières éludées. Il faut noter que le crépuscule du soir appartient à l'origine au secteur 3 et celui du matin au secteur 4.
Usage
La fonction essentielle du quadrant ottoman est de déterminer les heures de prières. Son mode d'emploi s'inspire en partie du quadrant vetustior et surtout de l'astrolabe.
Dans la démarche développée ci-dessous, on prendra l'exemple d'un quadrant tracé pour une latitude de 42° et utilisé le jour de l'entrée du Soleil dans le signe des Poissons ou du Scorpion.

Détermination de l'instant où doit être annoncée la prière de l'asr 1[N 20] :
- tendre le fil à plomb sur le repère A qui correspond à l'entrée du Soleil dans les signes zodiacaux des Poissons-Scorpion sur l'écliptique ;
- amener la perle en ce point ;
- l'arc de cercle de déclinaison solaire, lieu du Soleil pour la journée, a sensiblement pour rayon la hauteur méridienne de 37° définie par la position de la perle sur le fil ;
- cet arc de cercle coupe la courbe de l'asr 1 en B. Ce point permet de déterminer la hauteur (≈ 23°) et l'azimut (≈ 48°) de l'instant de la prière qui se lit sur le limbe : 45° ou 3h de l'après-midi (15° sur le limbe correspond à une heure équinoxiale). En visant le Soleil, le muezzin annoncera l'heure de la prière quand la perle recouvrira la courbe de l'asr 1.
Usage de la courbe des crépuscules :
d'abord, sur la figure précédente on voit qu'au jour défini, le lever et le coucher du Soleil, d'almucantarat 0°, donne sur le limbe un angle de 10° (3/4 d'heure). Le lever a donc lieu à 6 h 40 min et le coucher à 17 h 20 min.
Ensuite, pour les crépuscules, on trouve sur le limbe, à partir de l'intersection de l'arc de déclinaison avec la courbe des crépuscules, un angle de 14° (56 min). Ce qui permet de déterminer l'instant de l'aube, 5 h 04 min, par rabattement dans le secteur 4 et l'instant du crépuscule du soir, 18 h 56 min, par double rabattement dans le secteur 3[N 21].
Ainsi, sommairement, on peut déterminer les intervalles de temps où le muezzin peut annoncer les prières liées aux crépuscules.

Notes et références
Notes
- En gnomonique, à une date donnée, la déclinaison solaire est considérée comme constante ; sa valeur est celle du midi solaire du jour considéré.
- Il existe des tables donnant la correspondance entre la déclinaison solaire et les calendriers civil et/ou zodiacal ; on verra plus loin comment se dispenser de ces tables.
- E. Poulle indique que « c'est l'érudition moderne qui a précisé les termes latins employés, et que le quadrans vetustissimus a été forgé par J.-M Millas-Villacrosa en 1932. »
- vetustior est le comparatif de vetus.
- La méthode des rabattements des cercles de l'astrolabe se retrouvera un peu plus tard en Occident sur le quadrant nouveau proposé par Profatius en 1288.
- Les angles de graduation de l'écliptique sont calculés à partir de la formule où α est l'ascension droite, ε l'inclinaison de l'écliptique et λ la longitude écliptique.
- Cette table est calculée à partir d'une formule moderne donnant obliquité de l'écliptique, longitude et déclinaison du Soleil en fonction du jour julien considéré.
- Pour information, ε = 23°35' = 23,583° correspond à une obliquité des années 900 - époque de création de ce type de quadrant ?
- À titre indicatif, les valeurs angulaires « vraies » de chaque signe, correspondant à l'ascension droite du Soleil sur l'écliptique vers les années 1150, du Capricorne au Gémeaux sont sensiblement dans l'ordre, de 32,2°, 29,9°, 27,9°, 27,9°, 29,9°, 32,2°.
- L'obtention de cette table est dite suivre la relation (1) donnée précédemment. Pour obtenir ces hauteurs, la déclinaison, non précisée, doit être connue ; est-elle obtenue graphiquement ou à partir de la relation ? Relation où δ est la déclinaison, ε l'obliquité de l'écliptique et λ la longitude écliptique du Soleil.
- C'est aussi vers midi que la mesure de hauteur - comme sur tout cadran de hauteur - est la plus incertaine ; les deux « imprécisions » se « cumulent » statistiquement, ce qui détériore encore plus le résultat.
- Les point i2, i4, i6 ne sont pas représenter pour ne pas surcharger la figure.
- Par exemple, à la fin de la première heure temporaire alors ; pour , alors ; pour , alors .
- Voir le tableau précédent.
- Les graduations de « hauteur » tracées sur l'alidade n'ont aucun rapport avec le problème traité.
- Sur l'instrument, l'entrée dans le signe du Bélier correspond à la date du 13 mars du calendrier julien. Ceci permet de dater la table calendaire à partir de laquelle a été tracé le quadrant, vers les années 1300 - Voir la source Wiki.
- La figure, non représentée, se trouve en planche I, dans l'ouvrage d'Anthiome et Sottas
- Ces 17° n'ont pas de rapport avec les 17° du Taureau repérant le lieu du Soleil au 1er mai
- Voir des illustrations en ligne.
- Cet instant correspond aussi à la limite de fin de la prière de dhohr.
- Cette petite gymnastique intellectuelle était aussi nécessaire pour lire l'heure sur les courbes des prières éludées.
Références
- D'après R. D'Hollander 1999, p. 213.
- D'après Philippe Dutarte 2006, p. 206-209.
- D'après Philippe Dutarte 2006, p. 208
- Emmanuel Poulle, Les sources astronomiques, Turnhout-Belgium, Brepols, , p. 36, 40, 42.
- Catherine Jacquemard, Olivier Desbordes et Alain Hairie 2007, p. 79
- R. D'Hollander 1999, p. 213.
- Sur le modèle théorique voir : Gérard Aubry 2019, p. _ _ _ ?
- La formule de référence, complexe, est donnée dans Denis Savoie, La gnomonique, Paris, Les Belles Lettres, coll. « L'Âne d'or », , 521 p. (ISBN 978-2-251-42030-1), p. 56-58.
- Rappel : Catherine Jacquemard, Olivier Desbordes et Alain Hairie 2007, p. 79
- Sur l'erreur sur la lecture de l'heure voir : Gérard Aubry 2019, p. _ _ _ ?
- Sur l'incertitude sur la lecture de l'heure voir : Gérard Aubry 2019, p. _ _ _ ?
- Voir la référence BnF, et sa publication par Paul Tannery, lire en ligne
- D'après R. D'Hollander 1999, p. 137.
- D'après Philippe Dutarte 2006, p. 209 ; voir aussi R. D'Hollander 1999, p. 143.
- D'après R. D'Hollander 1999, p. 144.
- D'après R. D'Hollander 1999, p. 214-215 et David A. King 2002.
- David A. King 2002, p. 237-238.
- David A. King 2002, p. 240-241.
- R. D'Hollander 1999, p. 233.
- Voir R. D'Hollander 1999, p. 230-233 pour une présentation détaillée ; source : Anthiaume & Sottas, L'astrolabe-quadrant du Musée des Antiquités de Rouen, Paris, G. Thomas, (lire en ligne).
 .
. - D'après Philippe Dutarte 2006, p. 209-213.
- Illustration en ligne du British Museum.
- D'après un article temporaire de Bonhams Archive ?
- Voir le site de Whipple Collections, Sur le quadrant de Gunter.
- Voir une édition de 1721 sur l'utilisation du quadrant :Google books : The Description and Use of... Gunter's Quadrant
- Un applet sur le sujet;
- Un quadrant de 1657. ; Image du British Museum (ca 1800).
- Pour une description détaillée voir : Philippe Dutarte 2006, p. 219-231.
- D'après Philippe Dutarte 2006, p. 219-224.
- Pour les heures des prières voir Philippe Dutarte 2006, p. 224-227.
Voir aussi
Bibliographie
- R. D'Hollander, L'Astrolabe : Histoire, théorie et pratique, Paris, Institut océanographique, (ISBN 2-903581-19-3).
 .
. - Philippe Dutarte, Les instruments de l'astronomie ancienne de l’Antiquité à la Renaissance, Paris, Vuibert, , 294 p. (ISBN 2-7117-7164-4).
 .
. - Catherine Jacquemard, Olivier Desbordes et Alain Hairie, Du quadrant vetustior à l’horologium viatorum d’Hermann de Reichenau : étude du manuscrit Vaticano, BAV Ott. lat. 1631, f. 16-17v, vol. 23, Caen, Kentron, (lire en ligne), p. 79-124.
 .
. - Gérard Aubry, Le quadrant « vetustior », vol. 39, Paris, Cadran-Info - Société Astronomique de France, .
 .
. - (en) David A. King, A Vetustissimus Arabic Treatise on the Quadrans Vetus, vol. 33, Journal for the History of Astronomy, (lire en ligne), p. 237-255.
 .
.
Articles connexes
Liens externes
- Approche générale, images
- Michel Lalos (voir : Types de cadrans solaires. Cadrans de hauteur. Quadrants), « Gnomonique un peu de théorie : Quadrants », sur Cadrans solaires - La mesure du temps, s.l., Michel Lalos (site personnel hébergé par Free) (consulté en )
- Musée de Greenwich (40 quadrants)
- Quadrants à heures inégales
Quadrant vetustior :
Quadrant ancien :
Quadrant nouveau ou astrolabe-quadrant :
- Quadrants à heures égales
- Quadrant de Richard II
- Quadrant au tracé rectiligne XVIIe siècle RMN
- Quadrants ottomans
- Quadrant sinus