Quadrant astronomique
Le quadrant astronomique ou quart de cercle[N 1] est un ancien instrument de mesure angulaire de la famille des quadrants employé dans les observatoires astronomiques.

À l'origine, cet instrument permettait de mesurer la hauteur d'un objet visé. Connu dans l'Antiquité, il est développé, jusqu'au gigantisme, par les Arabes. Introduit en Occident au Moyen Âge, il sera un des instruments astronomiques privilégiés de Tycho Brahe. Plus tard, des perfectionnements multiples, comme l'adjonction de lunettes de visée, le porteront au maximum de ses possibilités, mais favoriseront aussi l'apparition de transfuges : lunettes méridiennes par exemple. Ces innovations scelleront la disparition progressive et pratiquement définitive du quadrant astronomique au XIXe siècle.
Cet instrument peut être fixe : quadrant mural, ou avoir quelques degrés de mobilité : quadrant pivotant, quadrant pivotant azimutal, quadrant sur rotule. Vu ses dimensions, cet instruments est, par principe, le plus exact des anciens quadrants[1].
Histoire et évolution
Dans l'Antiquité
Dans l'Antiquité, les premiers quadrants seraient apparus - sous une forme archaïque - chez les Ioniens pour certains auteurs. Cependant les graduations en degrés sur les instruments d'observation n'apparaissent qu'au IIe siècle av. J.-C. Cette division du cercle est le fait d'Hipparque qui emploie des armilles pour ses mesures astronomiques ; mais le quadrant, comprenant un secteur gradué, n'est pas pour autant cité comme un de ses instruments[2].
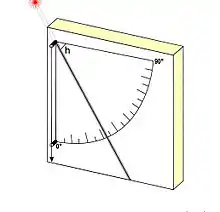
Ce n'est qu'au IIe siècle que l'existence du quadrant est prouvée. Ptolémée, dans l'Almageste, décrit le premier instrument, un peu particulier, qui lui sert à mesurer la hauteur méridienne du soleil[3]. Il est constitué d'un parallélépipède rectangle de pierre ou de bois, avec une face bien polie sur laquelle est tracé le secteur gradué. Au centre du cercle est emmanchée, perpendiculairement, une pige cylindrique ou « gnomon » ; une autre l'est au point zéro du secteur gradué. Le bloc est « calé » verticalement par un fil à plomb et au niveau d'eau, ceci dans le plan méridien tracé au sol. La lecture de la hauteur se fait « en marquant le milieu de l'ombre » laissée par la pige supérieure sur la face du bloc de pierre. Ptolémée trouve que cette façon de mesurer est « plus commode » que d'employer des « cercles » ou armilles. En effet la mesure au cercle s'effectue par l'intermédiaire de pinnules de visée, ce qui est dangereux pour l'œil, ou par de petits prismes, ce qui peut être moins précis à la lecture[N 2]. Ptolémée ne donne pas les dimensions de son quadrant, mais il indique que le secteur gradué est marqué « des degrés et de ses subdivisions » - ce qui implique, au minimum, une division du degré en 3 fois 20'. Cette indication tendrait à montrer que le quadrant fait au minimum 50 cm de rayon (soit un arc de 8,7 mm pour 1°), ce qui lui assurerait un poids de 125 kg pour un quadrant en pierre d'une largeur de 20 cm. Ainsi la stabilité de ce grand quadrant serait-elle assurée.
Le mesurage de la hauteur méridienne hm du soleil aux équinoxes permet alors de calculer la valeur approchée de la latitude φ du lieu : hm = 90° - φ. Ptolémée ne donne pas dans le chapitre X de l'Almageste de valeurs chiffrées, ni pour la hauteur méridienne, ni pour la latitude. D'autre part, les hauteurs méridiennes au solstice d'été hm max. et d'hiver hm min. donnent :
- une valeur plus exacte de la latitude φ = (hm max. + hm min.) / 2 ;
- l'obliquité de l'écliptique ε = (hm max. - hm min.) / 2.
Ptolémée trouve pour 2ε des valeurs comprises entre 47° 1⁄3 et 47° 3⁄4 , ce qui lui donne pour l'obliquité de l'écliptique ε une valeur comprise entre 23,665° et 23,875°[N 3].
Dans le monde arabe
Les astronomes arabes s'appuyant sur les écrits de Ptolémée, s'inspirent de ses instruments, les améliorent et en construisent de nouveaux. Ils emploient, entre autres, des quadrants gigantesques dans leurs observatoires.
| N° | Quadrant | Nbre | Observatoire(s) | Date | Notes |
|---|---|---|---|---|---|
| 1 | non documenté | Damas, Bagdad | IXe siècle | ||
| 2 | mural | 1 | Ar-Raqqa en Syrie | Xe siècle | |
| 3 | mural | 1 | Ray (Téhéran) en Iran | Xe siècle | r = 20 m ; 1° = 35 cm ; 10" = 1 mm |
| 4 | mural | 1 | Maragha en Iran | XIIIe siècle | r = 18 m ; 1° = 31,5 cm ; 6" = 0,5 mm |
| 5 | double azimutal | 1 | d° | XIIIe siècle | |
| 6 | mural | 1 | Samarcande en Ouzbékistan | XVe siècle | r = 40 m ; 1° = 70 cm ; 6" = 1,2 mm |
| 7 | azimutal | 1 | d° | XVe siècle | |
| 8 | double mural[N 4] | 1 | Istanbul en Turquie | XVIe siècle | |
| 9 | pivotant | 1 | d° | XVIe siècle | r = 4,5 m ; 1° = 8 cm ; 1' = 1,3 mm |
Les quadrants muraux sont fixes. Ils sont donc placés suivant un plan privilégié qui est le plan du méridien du lieu d'implantation :
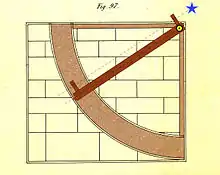
Les muraux munis d'une alidade à pinnules permettent de mesurer la hauteur méridienne des astres. Leur exactitude est fonction de leur grandeur : un mural, décrit dans un manuscrit arabe[5], mesure environ 3 m de rayon et son limbe est divisé en minutes (un arc de 1° mesure 52 mm et 1' mesure 0,9 mm : 1' est ici la résolution de l'instrument).
D'autres muraux, sans alidade, permettent de mesurer la hauteur méridienne du soleil en utilisant le principe de la chambre noire - principe employé aussi dans les grandes méridiennes que l'on trouve dans les églises : le mural est plongé dans l'obscurité d'un bâtiment dédié ; un trou de petit diamètre, situé au centre théorique du quadrant, laisse passer les rayons du soleil qui vont former une tache de lumière « circulaire » sur le secteur d'observation. Le centre du disque lumineux donne la hauteur du soleil à midi en passant sur la ligne méridienne. Cette hauteur hm permet, comme vu précédemment, de déterminer la latitude φ, l'inclinaison de l'écliptique ε et aussi la déclinaison solaire δ pour chaque jour, à midi vrai, déclinaison[N 5] qui sera bien utile pour faire le point en navigation. Les muraux (3), (4), (6) sont de ce type.
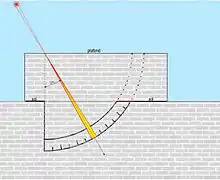
- le mural (3) de Ray est bien documenté[6] ; de 20 m de rayon, il est gradué uniquement sur le secteur fonctionnel, soit de 0 à 60°, d'où son nom de « sextant ». C'est alors la hauteur zénithale à midi zm qui est lue au lieu de son complément hm. La résolution est de 10", mais l'incertitude de mesure, inconnue, doit être bien supérieure[N 6]. Pour réduire l'incertitude du mesurage, les astronomes employaient un cercle réticulé, de la dimension de la tache de lumière, qu'ils déplaçaient sur l'image du soleil. La détection du lieu de l'intersection était de ce fait plus exacte.
- le mural (4) de Maragha est aussi bien documenté[7] ; il comporte en son centre « une ouverture circulaire ou oculus dont le diamètre est de 1/6 de coudée [75 mm] avec un « tuyau » [en vrai, un petit anneau calibré] , il se composait d'un arc de 60°, divisé de 6 en 6" » ;
- le mural (6) de Samarcande est aussi documenté[8] ; ses fondations subsistent et peuvent se visiter. C'est le plus gigantesque. Il avait un rayon de 40 m, 1° mesurant 70 cm, sa résolution pouvait atteindre 3" au mieux. Les observations effectuées permirent notamment l'établissement des tables astronomiques d'Ulugh Beg.
 Ulugh Beg et le mural de Samarcande.
Ulugh Beg et le mural de Samarcande. Le mural aujourd'hui.
Le mural aujourd'hui. Quadrant pivotant, BnF, manuscrit Turc, 1580.
Quadrant pivotant, BnF, manuscrit Turc, 1580.
Les quadrants pivotants et azimutaux sont à alidade et peuvent tourner autour d'un axe vertical. Le quadrant (9) d'Istanbul est simplement pivotant[9], il permet de mesurer la hauteur d'un astre d'orientation quelconque. Les quadrants azimutaux sont montés sur un cercle gradué horizontal, le zéro étant dans le plan méridien. Ils permettent de mesurer l'azimut d'un astre simultanément avec sa hauteur. Le quadrant (5) de Maragha était double, il permettait de mesurer simultanément la position de 2 astres[10].
En Occident (et en Chine)
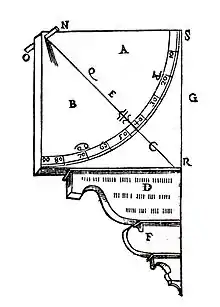

Dans le monde occidental, les quadrants apparaissent dès le XIIIe siècle. En 1283, Pierre de Limoges se sert d'un « grand quadrant ». Il est en bois et en laiton ; le limbe est gradué de 5 en 5 minutes[1]. En 1319, Jean de Murs utilise un « kardaga », grand quart de cercle d'un peu moins de 5 m, gradué sur un secteur de 15°. « il était dressé fixe sur une pierre et établi dans le plan méridien »[11]. Au début du XVe siècle, Jean Fusoris utilise un grand quadrant, chez Guillaume de Sens, à Paris, pour établir des tables de hauteur du soleil[12]. Les valeurs des tables sont conformes aux valeurs théoriques à ± 10 minutes de degré, ce qui peut correspondre grossièrement à une résolution de 2 minutes, soit un rayon du quadrant de 1,5 m.
Au XVIe siècle, Ignazio Danti place un quadrant astronomique dans le plan du méridien, sur la façade de l'église S.M. Novella, à Florence (en 1574). Ce quadrant est une réplique du quadrant de Ptolémée ; d'une surface d'environ 1,5 m², Danti s'en sert, entre autres, pour déterminer l'obliquité de l'écliptique avec, selon lui, beaucoup de précision ; valeur qu'il inscrit sur le socle du quadrant soit 23°26'49"55'" ! Il aurait dû trouver 23°29'44"[13]. Ce quadrant existe toujours aujourd'hui (2014).
Au XVIe siècle encore, Tycho Brahe utilise un grand nombre d'instruments d'observation[14] de dimensions imposantes dans son observatoire d'Uraniborg. Parmi les 22 instruments décrits dans son ouvrage, on ne compte pas moins de 8 quadrants différents sans compter les sextants :
 Petit quadrant pivotant à division de Nonius.
Petit quadrant pivotant à division de Nonius. Très grand quadrant pivotant
Très grand quadrant pivotant Quadrant moyen azimutal.
Quadrant moyen azimutal. Grand quadrant tournant azimutal.
Grand quadrant tournant azimutal. Très grand quadrant azimutal avec carré géométrique.
Très grand quadrant azimutal avec carré géométrique.
- 1 mural d'environ 2,25 m de rayon. Il possède un viseur mobile qui coulisse sur le limbe. Les degrés sont divisés en minutes et les minutes sont divisées en dix par « transversales » permettant une résolution de 5" (voir illustration d'en-tête) ;
- 2 pivotants : un petit « quadrans minor» avec divisions de Nonius et un grand « quadrans maximus» ;
- 5 azimutaux : de différentes tailles, avec ou sans transversales ; certains ont un double système de graduations du type « carré géométrique » pour avoir directement des valeurs trigonométriques des angles relevés (voir quadrant géométrique).
D'une façon générale, l'exactitude des mesures effectuées est de l'ordre de la minute d'angle ; « Tycho courait après la minute » d'après J-B Delambre[15].
Au XVIIe siècle, Hevelius, lui aussi se servira d'un grand nombre d'instruments du même type que Tycho. Ils illustrent son ouvrage Machinæ coelestis[16].
 Quadrant pivotant.
Quadrant pivotant.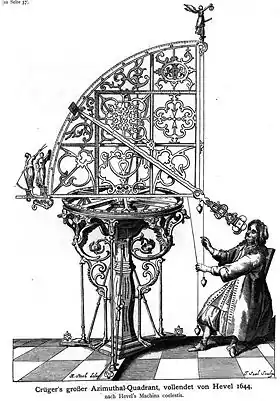 Quadrant pivotant azimutal.
Quadrant pivotant azimutal. Autre quadrant pivotant azimutal.
Autre quadrant pivotant azimutal. Grand quadrant sur rotule.
Grand quadrant sur rotule.
À la fin du XVIIe siècle, en Chine, Ferdinand Verbiest fait construire pour l'observatoire antique de Pékin un certain nombre d'instruments dont un quadrant pivotant de 3,6 m de rayon[17].
 Grand quadrant pivotant.
Grand quadrant pivotant.
Simultanément, en Occident, après l'apparition de la lunette de Galilée en 1609 et l'adjonction d'un réticule au foyer de l'instrument, vers 1670, par Picard, les astronomes adaptent des lunettes sur les quarts de cercle mobiles et, un peu plus tard, sur les quadrants astronomiques. Vers 1644, Hevelius, dans son observatoire, préfère encore l'alidade à pinnules, mais les progrès sur les lentilles des lunettes scelleront bientôt la disparition de ce type de matériel. Jean-Dominique Cassini fait construire un instrument azimutal avec lunette vers 1678 à l'Observatoire de Paris et Picard y fait installer un mural de 5 pieds de rayon (environ 1,6 m) qui ne sera opérationnel qu'en 1683, après sa mort. Flamsteed, la même année, fait installer un secteur mural de 135° à l'Observatoire royal de Greenwich. En 1721, est décrit dans le détail un petit quart de cercle mural de l'Académie des Sciences. C'est un quadrant de 1,15 m à deux lunettes qui permet d'apprécier la minute par les transversales[18].


De plus, l'adjonction d'un micromètre, dont l'invention date de 1640, augmente considérablement la résolution métrologique, ceci vers les années 1730. « Les grands appareils d'observation de cette époque sont fabriqués par une quinzaine de spécialistes, une dizaine en Angleterre et quatre ou cinq en France ». Parmi eux : Graham, John Bird, Dollond en Angleterre et Langlois, Canivet, Lenoir en France. Les derniers muraux sont de leurs fabrications. Ainsi, Bird, en Angleterre, en fait plusieurs de 2,5 m, tout en laiton, au prix de 8 000 livres [19]. Certains d'entre eux existent toujours ; Canivet, en France, « en fait de 6 pieds [2 m], au prix de 5 000 livres[20], qui seront considérés comme les meilleurs après ceux du constructeur anglais. ». Le Monnier adapte, pour un quadrant de Bird, une articulation sphérique qui permet de faire pivoter le quadrant de 180° sur son bloc de maçonnerie [21].
Les progrès de la construction font que la résolution de ces instruments descendra en-dessous de la seconde de degré à la fin du XVIIIe siècle , mais malgré tout, ce type de quadrant sera remplacé progressivement par les instruments méridiens, encore plus exacts, et dont certains sont toujours en activité au XXIe siècle[22].
Notes et références
Notes
- Dans « l'école française d'astronomie », au XVIIIe siècle, cet instrument est appelé « quart de cercle » ; il est cité comme tel par Le Monnier dans Description et usage des instruments d'astronomie, 1774, Lien permanent. Le terme « quadrant » est plutôt de culture anglaise.
- D'autre part, à encombrement égal, le quadrant est 2 fois plus précis : un arc de 1° sur un cercle d'un diamètre de 1 m mesure 8,7 mm et le même arc sur un quadrant d'un rayon de 1 m mesure 17,4 mm.
- Il trouve une valeur moyenne de 23,854° mais adopte 23,856° ou 23° 51' 20", valeur obtenue par Eratosthène et admise par Hipparque, alors qu'il aurait dû trouver 23,678° ou 23°40'42" (d'après R. d'Hollander op. cit. p. 251).
- Probablement : l'un orienté sud, l'autre orienté nord.
- La déclinaison du soleil varie entre ±ε valeurs atteintes aux solstices en passant par 0, valeur aux équinoxes ; la relation qui lie les trois variables est la suivante : φ = δ + 90 - hm pour un lieu situé au nord du tropique du Cancer.
- Au XXIe siècle, on admet, en métrologie, que la résolution d'un instrument soit environ 10 fois inférieure à la tolérance à vérifier.
Références
- Dutarte, Op. cit. en bibliographie : Les quadrants, p. 183-231.
- Raymond d'Hollander, Sciences géographiques dans l'Antiquité : connaissance du monde, conception de l'univers, Paris, Aft, , 465 p. (ISBN 2-901264-53-0), p. 157-179
- Ptolémée traduction Halma, Composition mathématique, t. 1, livre I, chapitre X, Paris, Hermann, (lire en ligne), p. 47-48
- L. Am. Sédillot, Mémoires de l'académie royale : Mémoire sur les instruments astronomiques des Arabes, t. 1, Paris, ; Dutarte, Op. cit., p. 186-189.
- Ms. ar. n° 1157, Bibliothèque Nationale de Paris, cité par L. Am. Sédillot, Op. cit. (lire en ligne), p. 194, 195
- Dutarte cite al-Biruni comme référence.
- D'après Abu Ali al-Hasan al-Marrakushi (en) dans L. Am. Sédillot, Op. cit., t. 1 (lire en ligne), p. 202-206
- Dutarte cite al-Kashi comme référence.
- Denis Savoie, dans ouvrage collectif, L'âge d'or des sciences arabes : Les astrolabes, t. 1, Paris, Actes Sud et Institut du monde arabe, (ISBN 2-7427-5672-8), p. 96
- L. Am. Sédillot, Op. cit., t. 1 (lire en ligne), p. 199-200
- Emmanuel Poulle, Les astronomes parisiens au XIVe siècle et l'astronomie alphonsine : Jean de Murs, t. 43, Paris, Boccard, coll. « Histoire littéraire de la France », (ISBN 2-87754-172-X), p. 21
- D'après Emmanuel Poulle, Un constructeur d'instruments astronomiques au XVe siècle : Jean Fusoris, Paris, Champion, ; étude et analyse de Gérard Aubry, Les cadrans de Jean Fusoris, Paris, Société Astronomique de France, coll. « Cadran-Info », 2008-2009
- John L. Heilbron, Astronomie et églises, Paris, Belin, coll. « Pour la science », (ISBN 2-7011-2814-5), p. 70-71 ; source : Danti, Primo volume dell'uso e fabbrica dell'astrolabio, Florence, Giunti,
- (la) Tycho Brahé, Astromiae instauratae mechanica, , ouvrage traduit par Jean Peyroux, Mécanique de l'astronomie rénovée, Bordeaux, Bergeret,
- Jean-Baptiste Delambre, Histoire de l'astronomie moderne, t. 1, Paris, Coursier, (lire en ligne), p. 233
- (la) Hevelius, Machinæ coelestis, (lire en ligne)
- Voir aussi les informations du site de l'observatoire de Pékin (traduire) :
- Maurice Daumas, Op. cit. en bibliographie, p. 68-84.
- Lalande, Astronomie, t. 1, Paris, (lire en ligne), xlix
- Lalande, Op. cit, dito.
- Pierre-Charles Le Monnier, Description et usage des principaux instruments d'astronomie, Paris, (lire en ligne)
- Maurice Daumas, Op. cit., p. 230-239
Voir aussi
Bibliographie
![]() : document utilisé comme source pour la rédaction de cet article.
: document utilisé comme source pour la rédaction de cet article.
 Philippe Dutarte, Les instruments de l'astronomie ancienne, de l'Antiquité à la Renaissance, Paris, Vuibert, , 294 p. (ISBN 2-7117-7164-4).
Philippe Dutarte, Les instruments de l'astronomie ancienne, de l'Antiquité à la Renaissance, Paris, Vuibert, , 294 p. (ISBN 2-7117-7164-4). Maurice Daumas, Les instruments scientifiques aux XVIIe et XVIIIe siècles, Paris, P.U.F., .
Maurice Daumas, Les instruments scientifiques aux XVIIe et XVIIIe siècles, Paris, P.U.F., . (en) David A. King, Islamic Astronomical Instruments, Londres, Variorum, (présentation en ligne)
(en) David A. King, Islamic Astronomical Instruments, Londres, Variorum, (présentation en ligne)