Navigation astronomique
La navigation astronomique est une technique de navigation qui consiste à déterminer sa position à l'aide de l'observation des astres et la mesure de leur hauteur (c'est-à-dire l'angle entre la direction de l'astre et l'horizon). Elle est utilisée traditionnellement par les Polynésiens[1] (voir Peuplement de l'Océanie > Navigations austronésiennes). En Europe, elle est mise au point à partir de la Renaissance par les navigateurs portugais.
En navigation maritime, comme autrefois en navigation aérienne[2], la détermination de la position nécessite l'emploi d'un sextant, la consultation d'éphémérides, un identificateur d'étoiles, la mesure de l'heure exacte, et l'application de formules de mathématiques[3].
En navigation spatiale, l'engin spatial embarque un viseur d'étoiles.
Ces méthodes, indépendantes de tout système extérieur, peuvent être mises en œuvre en complète autonomie et sans aucun appareil électrique. La navigation astronomique n'est dépendante que des seules conditions météorologiques : sans astres visibles, aucune mesure n'est possible.
La navigation astronomique est restée longtemps l'unique technique permettant aux navigateurs de se situer hors de vue de terre, à condition que l'heure soit connue avec une très bonne précision et que leur estime soit bien tenue. Le Soleil est l'astre utilisé le plus souvent, mais les mesures les plus précises sont obtenues à l'aide d'autres étoiles, au crépuscule parce qu'il est nécessaire que l'horizon soit visible. Il est aussi possible de viser la Lune et les planètes, (avec des résultats moins précis) pourvu qu'elles soient décrites dans des éphémérides. L'observation de plusieurs étoiles permet d'obtenir une bonne position à l'aube et au coucher du soleil (point crépusculaire) ainsi que celle du Soleil, à toute heure de la journée ou à la méridienne (point à midi).
Principe de base
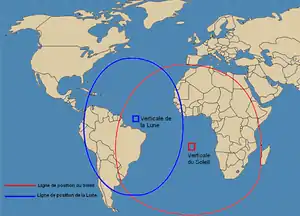
Le lieu des points, d'où l'on relève un astre donné à un instant donné à une certaine hauteur au-dessus de l'horizon, dessine un cercle sur la sphère terrestre. Le centre de ce cercle correspond à la position à laquelle cet astre est au zénith. On connaît avec exactitude (par les éphémérides) la latitude et la longitude de cette position[4], aussi appelé "pied" de l'astre ou point substellaire. Le rayon du cercle est le produit du rayon de la Terre et de la distance zénithale de l'astre, où , étant la hauteur de l'astre au-dessus de l'horizon.
En mesurant plusieurs hauteurs d'astres différents ou en établissant des mesures du même astre à des heures différentes, il est possible de déterminer une position à l'intersection de ces différents cercles. Des méthodes de calculs, à partir de tables de logarithmes ou d'une calculatrice scientifique, permettent de déterminer ces positions à partir des angles mesurés.
Mesure de la hauteur au sextant
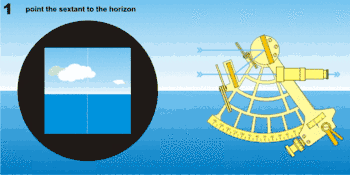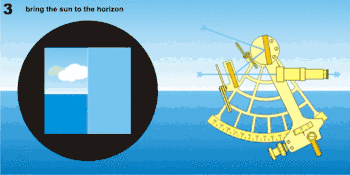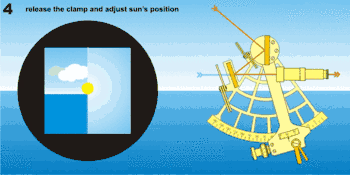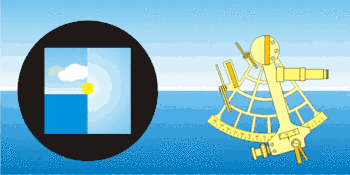
La précision des outils de mesure a évolué avec le temps. Une méthode simple et très approximative est de lever la main avec le bras tendu. La largeur d'un doigt correspondant environ à 1,5°. La nécessité de disposer d'outils de mesure plus précis a entrainé le développement de nombreux outils de plus en plus performant, le bâton de Jacob, le kamal, le quadrant, l'astrolabe, l'octant et aujourd'hui le sextant, qui permet par un jeu de miroirs de mesurer la hauteur de l'astre au-dessus de l'horizon avec une bonne précision.

La lecture d'un sextant bien réglé permet une précision de 0,2' d'arc. En théorie, un observateur peut donc déterminer sa position avec une précision de 0,2 milles marins[5]. Dans la pratique, les navigateurs obtiennent une précision de l'ordre de 1 ou 2 milles marins (mouvements du navire, houle, horizon plus ou moins net, imprécisions de l'heure).
L'observation consiste à «faire descendre» l'image réfléchie de l'astre sur l'horizon et la faire tangenter l'horizon (d'où le mouvement de balancier de la main qui tient le sextant). S'il s'agit du Soleil ou de la Lune, on fait tangenter son bord inférieur ou supérieur. Pour les étoiles et les planètes, il est conseillé de «monter l'horizon» au voisinage de l'astre en retournant le sextant, puis d'observer normalement.
La hauteur mesurée au sextant doit être corrigée d'un certain nombre de paramètres propres à l'optique du sextant utilisé, à la hauteur de l'observateur au-dessus de l'eau, à la réfraction astronomique et à l'astre visé.
La hauteur vraie est déduite de la hauteur mesurée par la formule :
- avec :
- , l'excentricité du sextant, affichée dans la boîte du sextant ;
- , la collimation du sextant à mesurer et éventuellement à corriger avant chaque observation ;
- , la dépression de l'horizon, fonction de la hauteur de l'œil de l'observateur, donné par les éphémérides ;
- , la réfraction astronomique ;
- , la parallaxe (négligeable pour les étoiles et les planètes) ;
- , le demi-diamètre (apparent) de la Lune ou du Soleil, affecté du signe + si on a visé le bord inférieur, du signe - si on visé le bord supérieur.
- Pour le Soleil, les éphémérides donnent la valeur journalière de ainsi que la somme ; étant le demi-diamètre moyen et on applique une deuxième correction : pour le bord inférieur et pour le bord supérieur.
- Pour la Lune on applique une formule analogue avec des valeurs données par les éphémérides.
- Pour les étoiles et planètes : est négligeable ; est négligeable, sauf pour Mars et Vénus. La somme est fournie par les éphémérides ainsi que la valeur de pour Mars et Vénus.
La droite de hauteur
On a vu que le lieu des points, d'où l'on relève un astre donné à un moment donné à une hauteur donnée est un cercle sur la sphère terrestre. Ce cercle, dit cercle de hauteur, ne peut généralement pas être tracé entièrement pour des raisons matérielles (taille et planéité des cartes utilisées) mais, pour définir une position réelle, il suffit d'en tracer un arc proche de la position estimée de l'observateur. En pratique, cet arc peut être confondu avec sa tangente, à plusieurs conditions : observation de l'astre à une hauteur au-dessus de l'horizon inférieure à 65° et longueur inférieure à 60 milles[6]. Cette portion de tangente est appelée « droite de hauteur ».
Le calcul consiste alors à déterminer à partir de sa position estimée la hauteur à laquelle on devrait observer l'astre et à la comparer à la hauteur observée . La différence est appelée intercept (en minutes d'angle, et 1'= 1 mille marin). On trace la droite de hauteur depuis sa position estimée perpendiculairement à l'azimut d'observation de l'astre à une distance égale à l'intercept (à l'opposé, si négatif).
La hauteur estimée est donnée par la formule :
- avec :
- , la latitude du point estimée à l'heure de l'observation ;
- , la déclinaison de l'astre à l'heure de l'observation, donnée par les éphémérides
- , l'angle horaire de l'astre à l'heure de l'observation et à la longitude estimée :
- pour le Soleil, la Lune et les planètes principales : ; l'angle horaire au méridien d'origine est donné par les éphémérides
- pour les étoiles : ; l'angle horaire du point vernal (temps sidéral) au méridien origine et l'ascension verse de l'étoile , , sont donnés par les éphémérides.
Autrefois, le calcul était effectué au moyen de tables logarithmiques spécifiques (tables de Friocourt [7], tables 900 qui ne sont plus éditées ou HO 211 du Hydrographic Office de l'U.S. Navy). On pouvait aussi utiliser des tables, comme les HO-249, donnant des résultats pré-calculés pour un très grand nombre de points du globe. Dans ce cas, on n'utilisait pas sa position estimée mais la position la plus proche disponible dans la table. Aujourd'hui, on peut utiliser une calculette scientifique ou un logiciel adhoc sur micro-ordinateur.
De jour, on relève le Soleil à différents instants en rapportant le déplacement du navire, et généralement, on couple ces observations avec une hauteur méridienne.
À l'aube ou au coucher du soleil, on repère à l'identificateur d'étoiles les astres qui seront visibles pendant la période crépusculaire ainsi que les secteurs du ciel à surveiller pour les identifier. Puis on vise successivement ces étoiles et planètes. Ce point crépusculaire, où les observations sont presque simultanées, n'est pas entaché de l'erreur due à l'incertitude de l'estime entre chaque observation comme les droites du matin et la méridienne. On calcule l'intercept en utilisant pour chaque droite le même point estimé, à l'heure de la dernière observation, mais on reporte sur la carte les azimuts et intercepts depuis les points estimés dans l'ordre inverse des instants d'observation (méthode dite du point estimé).
Le point à midi
La méridienne
L'observation d'un astre à son passage supérieur dans le méridien du lieu permet de déterminer la latitude par la simple addition algébrique de la distance zénithale et de la déclinaison de l'astre :
- étant la hauteur et la déclinaison de l'astre, donnée par les éphémérides. La distance zénithale est affectée du signe du pôle auquel on tourne le dos pour l'observation.
Le plan du méridien n'étant pas matérialisable en mer, le passage de l'astre dans ce plan est défini par l'heure, heure qui n'a pas besoin d'être connue avec une grande précision[8] puisque la distance zénithale de l'astre varie peu aux environs du passage.
Pratiquement, cette observation n'est réalisable qu'avec le Soleil, car la culmination d'autres astres ne sera observable que de nuit, alors que l'horizon n'est, en général, plus visible. On peut observer la méridienne entre une minute avant et une minute après l'heure calculée ; dans ces limites on notera la hauteur obtenue au moment où le contact est le meilleur.
Le report d'une ou plusieurs droites de hauteur observées dans la matinée permet avec la méridienne d'obtenir un point à midi.
Circumméridienne
Si l'observation de la méridienne n'a pas pu se faire (un nuage par exemple) dans les limites de temps (+ ou - 1 minute), la circumméridienne permet d'exploiter rapidement l'observation faite.
Circumzénithales correspondantes
Lorsqu'un astre culmine près du zénith , on peut déduire en quelques minutes la position du navire[9]. La latitude est la latitude méridienne et la longitude est déduite de l'heure de la culmination :
- avec :
- la longitude estimée ;
- la différence entre l'heure réelle et l'heure estimée de culmination
L'heure réelle de la culmination ne peut s'observer directement ; on l'obtient en prenant la moyenne des heures de passage à des hauteurs égales observées de part et d'autre du méridien, ni trop près parce que la variation de la hauteur serait peu sensible, ni trop loin parce que la moyenne des heures de passage s'écarterait trop de l'heure de la culmination.
- Calcul de l'heure précise (en temps universel) de la culmination au méridien (longitude estimée) :
- avec :
- , heure de passage de l'astre au méridien. Pour le Soleil le passage au méridien origine est donnée par les éphémérides ainsi que la variation journalière qui doit être pondérée de la longitude estimée ;
- , vitesse du navire en latitude (positive si composante nord)
- , variation de la déclinaison , donnée par les éphémérides
- commencer les observations à environ (13 min pour une distance zénithale entre 8 et 10° ; à diminuer progressivement et jusqu'à 6 min si elle est inférieure à 2°) en observant des hauteurs croissantes de 3' en 3' (à augmenter progressivement et jusqu'à 7' si la distance zénithale est inférieure à 2°) ;
- observer la hauteur de culmination ;
- observer la série des hauteurs décroissantes égales à celles prises avant la culmination ;
- calculer l'heure de culmination par la moyenne des heures de passage à hauteurs égales ; en tirer d'où
- calculer la latitude :
Navigation sans instruments
En 1965, à bord de Rehu Moana, le britannique David Lewis navigue de Tahiti jusqu'au nord de la Nouvelle-Zélande, en utilisant les méthodes de navigation des Polynésiens[10] - [11]. Sans sextant et sans compas, il parcourt près de 2000 milles, s'aidant notamment d'une table avec palier de coucher et de lever de soleil[12].
Notes et références
- Georges Boulinier et Geneviève Boulinier, « Les Polynésiens et la navigation astronomique », Journal de la Société des océanistes, t. 28, no 36, , p. 275–284 (lire en ligne)
- cette méthode n'est plus utilisée aujourd'hui en aéronautique, au profit des systèmes de positionnement radioélectriques terrestres ou par satellites. Les sextants utilisés en aéronautique - comme ceux utilisés dans les périscopes de sous-marins - devaient disposer d'un système gyroscopique donnant un horizon artificiel
- trigonométrie sphérique
- elles correspondent aux coordonnées horaires de l'astre : la latitude est égale à la déclinaison de l'astre et la longitude à son angle horaire
- puisque 1 mille correspond à 1' d'arc de grand cercle
- Navigation Astronomique M. DE KERVILER (C.R)
- Diverses tables utilisées depuis la fin du XIXe siècle
- d'où le grand intérêt de la méridienne et ce qui explique pourquoi, autrefois avant l'invention de chronomètres fiables au XVIIIe siècle, seule la latitude était connue avec précision en mer
- ne peut donc se pratiquer avec le Soleil qu'en zone tropicale et selon la saison
- S'orienter en mer sans instrument : le savoir-faire des tahitiens
- Science et savoir-faire, l'exemple de la navigation astronomique des Polynésiens
- (en) Ben Finney, Voyage of Rediscovery : A Cultural Odyssey through Polynesia, , 401 p. (ISBN 978-0-520-08002-7, lire en ligne), chap. 2 (« Experimental voyaging : Rehu Moana »), p. 35-36
Voir aussi
Articles connexes
Liens externes
- Ephémérides nautiques
- La navigation astronomique ? Mais, c'est très simple !
- et association Sail The World délivrent des logiciels gratuits de calculs de point astronomiques, d'éphémérides nautiques et d'identificateur d'étoiles.
- Du Kamal au GPS, une petite histoire de la navigation (site réalisé par le musée national de la Marine)