Pseudo-vecteur (mathématiques)
Dans un espace vectoriel de dimension 3, un pseudo-vecteur est un objet mathématique qui peut être représenté par une forme bilinéaire alternée ou par un tenseur antisymétrique d'ordre 2 ou, dans une base donnée, par une matrice antisymétrique. Il porte aussi le nom de bivecteur car il peut s'écrire comme le produit extérieur de deux formes linéaires. Si l'espace est euclidien et orienté, on lui fait correspondre un vecteur de l'espace appelé vecteur dual. On peut généraliser cela à toute dimension supérieure à 3.
Par exemple, la vitesse d'un point quelconque d'un solide en rotation dans l'espace est déterminée à l'aide d'un tenseur antisymétrique c'est-à-dire un pseudo-vecteur. Cependant, il est plus pratique d'utiliser son vecteur dual car celui-ci indique (entre autres) la direction de l'axe de rotation.
Notations
Les notions évoquées ci-dessus (et détaillées ci-dessous) s'organisent suivant le schéma suivant :
On désigne par un espace vectoriel de dimension . Afin de distinguer le produit extérieur et le produit vectoriel, on utilisera de façon exclusive la notation « » pour le produit extérieur (notation universelle donc incontournable) et la notation « » pour le produit vectoriel (notation extrêmement répandue, même si elle n'est pas encore utilisée partout et en particulier en France).
Espace dual
On note l'espace dual de c'est-à-dire l'espace vectoriel des formes linéaires sur ; ses éléments sont appelés des covecteurs. Cet espace vectoriel est aussi de dimension .
Base duale
On note la forme linéaire définie par si et si c'est-à-dire où est le tenseur de Kronecker. La base de l'espace dual est appelée base duale[1] de . Tout changement de base dans induit automatiquement le changement de sa base duale.
La position des indices dans la base n'est qu'une convention d'écriture parmi d'autres pour distinguer les vecteurs des deux bases. On aurait pu écrire ou par exemple. La convention choisie est celle qui est adaptée à l'écriture tensorielle et à la convention de sommation d'Einstein que l'on utilisera systématiquement.
Covariance et contravariance
En cohérence avec la dénomination tensorielle, un vecteur est un tenseur de type (1,0) et est dit contravariant ; de même un covecteur est un tenseur de type (0,1) et est dit covariant. C'est une définition intrinsèque (qui ne fait pas appel aux bases) et, comme toute définition, elle ne nécessite aucune justification[2].
- La base , constituée de vecteurs contravariants, est dite contravariante. Soit un vecteur ; ses coordonnées dans la base contravariante sont définies par et sont appelées les coordonnées contravariantes de . Dans , l'indice est dite en position contravariante (position haute) car il se réfère à des coordonnées contravariantes. On vérifie que .
- La base , constituée de vecteurs covariants, est dite covariante. Soit un covecteur ; ses coordonnées dans la base covariante sont définies par et sont appelées les coordonnées covariantes de . Dans , l'indice est dite en position covariante (position basse) car il se réfère à des coordonnées covariantes. On vérifie que .
Remarque : La position covariante ou contravariante d'un indice ne concerne que les coordonnées. En effet le vecteur est contravariant bien que l'indice soit en position basse. De même le covecteur est covariant bien que l'indice soit en position haute. Cela est simplement dû à la position des indices dans la convention d'Einstein.
Cas Euclidien
Isomorphismes musicaux
Dans le cas où est un espace vectoriel euclidien, à tout vecteur on fait correspondre la forme linéaire définie par (où « » est le produit scalaire). L'application linéaire est un isomorphisme de sur . On note son isomorphisme réciproque[3] et on définit sur un produit scalaire (que l'on note encore « »), appelé produit scalaire dual[4], par . Muni de ce produit scalaire, est un espace vectoriel euclidien et ces isomorphismes sont des isométries qui permettent d'identifier les espaces euclidiens et . Dans ce cas, quand on parle d'un vecteur (sans préciser davantage) on parle indifféremment d'un élément de ou d'un élément de ; on ne fait donc plus la distinction entre vecteurs et covecteurs.
Comme les formes linéaires sont identifiées à des vecteurs de , on a . Par exemple en dimension 3 on a et . Par conséquent où est le projeté orthogonal de sur la droite orthogonale au plan engendré par les vecteurs et .
On ne fait plus la distinction entre vecteur et covecteur c'est-à-dire que l'on ne fait plus la distinction entre vecteur contravariant et vecteur covariant. Par contre, comme la base est aussi une base de , les coordonnées d'un vecteur peuvent être calculées aussi bien dans la base que dans la base . Il faut donc toujours faire la distinction entre coordonnées covariantes et coordonnées contravariantes[5].
- Dans la base on a et ses coordonnées contravariantes vérifient .
- Dans la base on a et ses coordonnées covariantes vérifient .
Tenseur métrique
Le produit scalaire défini sur est un cas particulier de métrique[6]. Son tenseur associé est un tenseur covariant[7] appelé tenseur métrique. De même le produit scalaire dual, définit sur , est la métrique duale. Son tenseur associé est un tenseur contravariant appelé tenseur métrique dual.
On note les coordonnées dans la base du tenseur métrique et les coordonnées dans la base du tenseur métrique dual. Par définition des produits scalaires, on a les relations et . Ces tenseurs sont symétriques et on vérifie que , et . De plus, pour tout vecteur on a et . Ces formules montrent que la matrice est la matrice de changement de base de vers et que sa matrice inverse est .
Si et alors . Il est très inhabituel d'utiliser de cette manière les coordonnées issues de deux bases différentes, mais et ne sont pas indépendantes.
Par la suite il n'y a pas d'inconvénient à supposer que l'espace vectoriel est euclidien, le contexte permettant de savoir si la notion est utile ou non.
Algèbre extérieure
Formes extérieures
Soit un espace vectoriel. Pour on note l'espace vectoriel des p-formes alternées définies sur . On complète ces notations en posant , et pour . La dimension de l'espace vectoriel est avec la convention si . Les espaces vectoriels et ont donc la même dimension.
On note la somme directe de ces espaces vectoriels, c'est-à-dire
Les éléments de sont appelés des formes extérieures et ceux de des p-formes extérieures ou des p-vecteurs.
Produit extérieur
Le produit extérieur des covecteurs et est noté et est défini pour tout et tout par
C'est une forme bilinéaire car elle est linéaire en et linéaire en . Elle est de plus alternée car pour tout et donc antisymétrique, c'est-à-dire que
On peut définir le produit extérieur sur . Comme la définition formelle du produit extérieur est assez complexe[8], on se contentera d'en donner ses principales propriétés.
- le produit extérieur est une application bilinéaire de dans
- si et alors
- si et alors
- le produit extérieur est associatif c'est-à-dire que que l'on note alors plus simplement
Muni de cette loi, est une algèbre extérieure.
Pseudo-vecteur
Les éléments de sont appelés des bivecteurs. D'autre part est, tout comme , de dimension . Les éléments de sont pour cela appelés des pseudo-vecteurs. Le préfixe pseudo signale seulement que ces vecteurs, bien qu'appartenant à un espace vectoriel de même dimension que , ne sont pas des éléments de . Dans le cas , les pseudo-vecteurs sont donc des bivecteurs ; cette coïncidence n'a lieu que pour .
Soit et deux covecteurs. Comme et alors . Avec le vocabulaire ci-dessus, est donc un bivecteur. Dans le cas c'est aussi un pseudo-vecteur et tout pseudo-vecteur peut s'écrire comme le produit extérieur de deux covecteurs.
Bases des p-vecteurs
Étant donnée une base de , on a défini la base duale qui est donc la base canonique de associée à . Pour , on peut aussi définir une base de de façon naturelle (canonique) ; cependant, on ne peut définir aucun ordre naturel sur cette base.
Soit . Pour tout p-uplet ordonné vérifiant on pose . Puisque alors . Par exemple, et . L'ensemble des p-vecteurs où est un p-uplet ordonné est une base de notée . C'est la base covariante associée à la base et tout changement de base dans induit automatiquement un changement de base dans . Par abus de langage, les coordonnées d'un p-vecteur dans cette base sont appelées les coordonnées covariantes de dans (il est clair que c'est un abus de langage car ).
Pour , la base covariante de est . Tout bivecteur peut s'écrire (de manière unique) sous la forme ce qui donne
car on doit sommer sur l'ensemble des couples possibles vérifiant (convention d'Einstein généralisée).
Dans le cas où est un espace euclidien, les vecteurs sont identifiés à des covecteurs. De la même manière, on peut alors poser . La base constituée de ces p-vecteurs, notée , est la base contravariante associée à . Par abus de langage, les coordonnées d'un p-vecteur dans cette base sont appelées les coordonnées contravariantes de dans .
Pour , la base contravariante de est . Tout bivecteur peut s'écrire (de manière unique) sous la forme ce qui donne
Remarque : Il existe un isomorphisme canonique (c'est-à-dire indépendant des bases) entre les bivecteurs et les tenseurs antisymétrique d'ordre 2. En général on distingue ces tenseurs suivant qu'ils sont covariants, contravariants ou mixtes. Dans le cas d'un espace euclidien, ces distinctions sont sans objet car on identifie et . Cependant, même dans ce cas, il faut toujours faire la distinction entre les coordonnées contravariantes et covariantes car cela revient à indiquer dans quelle base ( ou ) les coordonnées sont calculées[5].
Espace orienté
Définition
L'espace vectoriel est, tout comme , de dimension 1. Ses éléments sont pour cela appelés des pseudo-scalaires. Là encore, le préfixe pseudo signale simplement que les éléments de ne sont pas des éléments de .
Une forme volume sur est un élément non nul de . Comme cet espace est de dimension 1, la relation d’équivalence définie sur par
permet de définir deux classes d’équivalence appelées orientations de . L'espace vectoriel muni de l'orientation est noté et appelé espace vectoriel orienté[9]. Même si le plus souvent, en l'absence d'ambiguïté, on note encore l'espace vectoriel orienté, il est mathématiquement important de distinguer l'espace vectoriel de l'espace vectoriel orienté .
Bases directes
Soit une base de et une forme volume. On dit que est directe (ou orientée positivement) si et indirecte (ou rétrograde ou orientée négativement) si . Cela est indépendant de .
On peut remarquer que la définition mathématique ci-dessus de l'orientation est intrinsèque. Elle ne fait pas intervenir les bases qui, de ce point de vue, sont des éléments étrangers à la notion. Il existe cependant une propriété concernant les bases qui sert parfois de définition alternative. Soit une base de (espace non orienté). L'ensemble des formes volumes telles que est une orientation. Cette orientation est appelée « orientation définie par ». Si on la note alors (par définition) est une base directe de l'espace orienté .
En physique, on peut ainsi définir une orientation telle que les bases directes soient des bases orientées à droite[10]. Pour cela on choisit une base orientée à droite (par la règle de la main droite, par exemple). D'après ce qui précède, cela détermine une orientation pour laquelle la base est directe. Cette orientation est identique à celle déterminée par le tire-bouchon de Maxwell.
Tenseur de Levi-Civita
Dans le cas d'un espace euclidien, on dit que est un vecteur unitaire si et seulement s'il existe une base orthonormale de notée telle que . Les propriétés du déterminant montrent alors que cette égalité est vérifiée pour toute base orthonormale. Il n'existe que deux vecteurs unitaires, chacun appartenant à une orientation. Soit un vecteur unitaire ; l'ensemble des formes volumes telles que est une orientation et on note l'espace vectoriel euclidien orienté par cette orientation. Cette définition de coïncide avec celle du tenseur de Levi-Civita qui peut donc aussi être appelé forme volume unité ou unité pseudo-scalaire.
Le tenseur de Levi-Civita permet de définir une bijection (canonique au signe près) appelée loi étoile de Hodge qui met en dualité les espaces vectoriels et . Ces espaces sont dits duaux l'un de l'autre, le contexte permettant de ne pas confondre avec l'espace dual .
Soit vecteurs de . L'expression est parfois notée et porte alors le nom de produit mixte. En dimension 3 on a, d'après la définition du produit vectoriel, la relation
Cette formule est à l'origine de l'appellation « produit mixte ». Les propriétés d'antisymétrie de donnent des relations analogues par permutation circulaire sur les indices.
Si les vecteurs sont coplanaires le résultat est nul. Sinon sa valeur absolue est égale au volume du parallélépipède construit sur ces trois vecteurs. Cela explique a posteriori le nom de « forme volume » donnée aux éléments de .
Espace euclidien orienté en dimension 3
Vecteur instantané de rotation
Soit un solide mobile indéformable et une base quelconque[11] de liée à Les vecteurs dépendent du temps mais les coordonnées du tenseur métrique dans cette base restent constantes. On note sa base duale. Comme alors . On note . D'où et car les sont les coordonnées covariantes de dans la base .
Si est un vecteur lié à alors où les ne dépendent pas du temps. D'où . Finalement
Il existe une forme bilinéaire alternée unique notée telle que (puisque les sont les coordonnées d'un tenseur, ne dépend pas de la base ). Par conséquent , c'est-à-dire que est un bivecteur et aussi un pseudo-vecteur puisque la dimension de est égale à 3.
D'un point de vue théorique, le pseudo-vecteur est l'outil adapté au problème mais il présente un double inconvénient. Tout d'abord, on ne travaille pas avec les objets eux-mêmes mais avec leurs coordonnées. Ensuite, il n'est pas facile de visualiser l'action d'un tel tenseur sur un schéma.
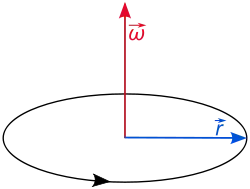
On cherche un outil ne présentant pas ces inconvénients ; pour cela on a besoin que l'espace soit orienté (on n'en avait pas besoin jusque là). Le dual de Hodge de est un vecteur et on pose (où est la loi étoile de Hodge). Les coordonnées de dans la base sont où est le tenseur de Levi-Civita. On obtient et . D'où
L'avantage est immédiat. On travaille avec un vecteur, qui est un objet plus simple qu'un tenseur (ici un bivecteur) et la formule n'utilise pas les coordonnées. Mais il faut être conscient que l'on a introduit artificiellement l'orientation de l'espace dans un problème qui, au départ, n'en dépend pas. Une première fois pour définir le vecteur , une seconde fois pour l'utiliser à l'aide du produit vectoriel. Le vecteur dual peut donc être considéré comme un simple intermédiaire de calcul qui a l'avantage de pouvoir être représenté graphiquement mais qui possède l'inconvénient de mal supporter les transformations, contrairement au pseudo-vecteur (voir ci-dessous).
Éléments correspondants
On reprend les notations précédentes. Soit une isométrie de indépendante du temps. Pour chaque élément défini sur on note avec un « ' » l'élément correspondant sur . Le plus souvent les éléments se correspondent à l'aide de l'isométrie, mais pas toujours.
On a . Si alors est la base image de car . De même est la base image de car . On a aussi et . Mais pour on a si est directe et si est indirecte.
Si l'isométrie est indirecte, le correspondant du vecteur dual est l'opposé de son image. En physique, on retrouve cette correspondance avec les vecteurs axiaux.
Dualité vecteur / pseudo-vecteur
En dimension 3, les espaces vectoriels et sont duaux c'est-à-dire que chaque pseudo-vecteur est associé par la loi étoile de Hodge à un vecteur et réciproquement. Si est un pseudo-vecteur, on note son vecteur dual. De même si et un vecteur on note son bivecteur dual. Les relations tensorielles entre les coordonnées sont
où est le tenseur de Levi-Civita. On a donc et .
En dimension 3, tout pseudo-vecteur peut s'écrire comme le produit extérieur de deux vecteurs. Le cas général se réduit donc à ce qui pourrait passer pour un cas particulier. Avec on obtient
c'est-à-dire que le produit vectoriel est le vecteur dual du produit extérieur[13].
Transformation isométrique
Soit une isométrie de . On note son déterminant. On a suivant que l'isométrie est directe ou indirecte.
- Pour le produit extérieur : [12]
- Pour le produit vectoriel :
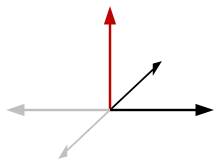
On a donc le schéma suivant :
Lorsque l'on transforme un bivecteur et son vecteur dual par une isométrie indirecte, le dual de l'image et l'image du dual sont des vecteurs opposés. Ce schéma ne fait que mettre en évidence la correspondance entre les deux vecteurs duaux ; il ne modifie pas l'image de qui est toujours et non .
En particulier si est l'inversion de l'espace[14], alors et l'opposé du produit n'est pas le produit des opposés. Cette relation n'a rien d'extraordinaire[15] et ne reflète pas un caractère "spécial" du produit vectoriel. Elle est, par exemple, vérifiée dans les réels : mais .
Représentation matricielle
Dans l'espace vectoriel des matrices carrées , on peut définir deux produits.
- le premier, noté " " ou (le plus souvent) par une absence de signe, correspond au produit matriciel usuel : ou
- le second, noté , est le crochet de Lie :
Il est à remarquer que le sous espace vectoriel des matrices antisymétriques n'est pas stable pour le produit usuel mais qu'il est stable pour le crochet de Lie. C'est-à-dire que si et sont antisymétriques alors est aussi antisymétrique.
Soit un espace euclidien et une base orthonormale directe de . Comme , on ne fait plus la distinction entre covariant et contravariant et la position des indices n'a plus aucune importance. On note la base canonique de , c'est-à-dire de l'espace vectoriel des pseudo-vecteurs (ou bien ici des bivecteurs). Par rapport à leurs bases respectives, un pseudo-vecteur et son vecteur dual peuvent être représentés par des matrices : une matrice (3,1) pour le vecteur et une matrice (3,3) antisymétrique pour le pseudo-vecteur.
Par rapport à leur bases respectives, un pseudo-vecteur et son vecteur dual ont presque[16] les mêmes coordonnées et les matrices se correspondent de façon simple. Par exemple si alors et donc . Les matrices correspondantes sont donc
et
Pour des raisons pratiques (cf les formules ci-dessous) on considère aussi la matrice transposée appelée la représentation antisymétrique de . Ces deux représentations sont utilisées ; par exemple, elles sont présentes comme sous matrices du tenseur de Maxwell selon la signature de la métrique.
On peut vérifier que
- : matrice vecteur colonne = vecteur colonne
- : matrice antisymétrique, matrice antisymétrique = matrice antisymétrique
- (cf. Exponentielle d'une matrice). C'est donc une matrice de rotation. Plus précisément, l'axe de rotation est de direction et l'angle de rotation (en radians) est égal à .
Remarque : Si la base n'est pas orthonormale ou même seulement indirecte, alors les coordonnées ne sont plus les mêmes et la correspondance ci-dessus n'est plus valable. Par exemple, rien de changé dans l'expression du produit extérieur (pseudo-vecteur) mais pour le produit vectoriel (vecteur dual) l'expression n'est plus aussi simple. La représentation matricielle n'a alors plus aucun intérêt.
Généralisation
Ce qui précède peut se généraliser aux Variétés différentiables. On parle alors de champ : champ de vecteurs, champ de covecteurs, champ de bivecteurs, etc.
Si est un système de coordonnées locales, alors la base associée des champs de vecteurs est où et la base duale (celle des covecteurs) est . On retrouve la position des indices.
La dérivée extérieure joue un rôle essentiel dans ce contexte. Exemple en dimension 3 : si est un champ de covecteurs alors est un champ de pseudo-vecteurs et est son champ de vecteurs duaux. Les relations correspondantes utilisant les coordonnées sont et .
De même, l'intégration des champs de p-vecteurs (qui portent alors le nom de p-formes différentielles) est un outil puissant ayant de nombreuses applications aussi bien en mathématiques qu'en physique (voir les articles détaillés).
Notes et références
- En physique et particulièrement en cristallographie, on parle de "base réciproque".
- Expliquer le choix des mots utilisés sort du cadre mathématique mais n'est pas dénué d'intérêt pour autant. Soit , et avec et donc . Si alors et donc . De même si alors et donc . On voit donc que les coordonnées du covecteur varient dans le même sens que la base alors que celles du vecteur varient en sens contraire.
- Ces isomorphismes canoniques sont appelés les isomorphismes musicauxBerger, p. 21.
- Ce produit scalaire est compatible avec la norme duale, c'est-à-dire que avec .
- Excepté si la base est orthonormale car alors .
- Une métrique (à ne pas confondre avec la distance d'un espace métrique) est une généralisation du produit scalaire (métriques euclidiennes). Elle intervient dans les espaces quadratiques (par exemple métrique de Minkowski, métriques lorentziennes) ainsi que dans les variétés différentiables.
- Landau, p. 295 §83.
- Godbillon, p. 23 §4.
- Contrairement à ce qui se passe en physique où l'orientation parait indépendante de l'espace physique, l'orientation d'un espace vectoriel orienté fait partie intégrante de cet espace et il n'est pas question d'envisager d'en changer. Cela n'aurait pas plus de sens que de vouloir changer la loi de multiplication dans .
- C'est la définition ci-dessus (mathématique) de « base directe » qui est utilisée ici. Cette phrase n'aurait aucun sens si les notions de « base directe » et de « base orientée à droite » étaient pris pour synonymes, comme c'est souvent le cas en physique.
- base quelconque : non nécessairement orthogonale ni même directe.
- Godbillon, p. 24 §4.
- On voit, une fois de plus, tout l'intérêt de pouvoir disposer de notations distinctes pour ces deux opérateurs à la fois si étroitement liés et si différents.
- Transformation qui à tout vecteur fait correspondre son opposé . A ne pas confondre avec l'inversion de la base : .
- C'est même la règle générale lorsque le produit est bilinéaire.
- Si l'on modifie de façon ad hoc la base canonique de en prenant , alors les coordonnées sont exactement les mêmes.
Voir aussi
Bibliographie
- Marcel Berger, Paul Gauduchon et Edmond Mazet, Le spectre d'une variété riemannienne, Berlin · Heidelberg, Springer-Verlag, coll. « Lecture Notes in Mathematics »,
- Claude Godbillon, Géométrie différentielle et mécanique analytique, Paris, Hermann, coll. « Méthode »,
- L.Landau et E.Lifchitz (trad. Edouard Gloukhian), Théorie du champ, Moscou, Mir,
Articles connexes
- Pseudovecteur ou vecteur axial
- Produit vectoriel
- Tenseur
- Analyse vectorielle
- Orientation
![{\displaystyle {\begin{matrix}&{\text{pseudo-vecteur}}&\displaystyle {\xleftarrow {} }\!{\xrightarrow[{\text{(loi étoile de Hodge)}}]{\displaystyle \star }}&{\text{vecteur dual}}\quad &\\&&{\bigg \uparrow }&&\\{\text{orientation}}&\xrightarrow {} &{\text{tenseur de Levi-Civita}}&\xleftarrow {} &{\text{produit scalaire}}\end{matrix}}}](https://img.franco.wiki/i/9e708c5a5c5aceb62991f7487bc2bff781817b7b.svg)





















































![{\displaystyle [g^{ij}]}](https://img.franco.wiki/i/192d42a2a8711bfd79663ad27c021ac79a471bdc.svg)
![{\displaystyle [g_{ij}]}](https://img.franco.wiki/i/7f7bb234146361057001a9e7c274a062f5e96a33.svg)














































































![{\displaystyle [x_{1},\cdots ,x_{n}]}](https://img.franco.wiki/i/33f38e11f6da502c3cc42ce03382ba854a229a58.svg)
![{\displaystyle [x_{1},x_{2},x_{3}]=(x_{1}\times x_{2})\centerdot x_{3}}](https://img.franco.wiki/i/8b52b34bb83d5b5a273c6674052a1e8d691b6267.svg)




































































![{\displaystyle {\begin{aligned}(h\,u\times h\,v)\centerdot t=&[h\,u,h\,v,t]\\=&\det(h)\,[u,v,h^{-1}t]\\=&\det(h)\,(u\times v)\centerdot h^{-1}t\\=&\det(h)\,(h^{-1})^{T}(u\times v)\centerdot t\end{aligned}}}](https://img.franco.wiki/i/98169207bc0a1d6d15e404848c7e795f0ce91a51.svg)













![[\ ,\ ]](https://img.franco.wiki/i/e7717dae012f042ad66888075df87a1ebac4392a.svg)
![{\displaystyle [X,Y]=XY-YX}](https://img.franco.wiki/i/838f73010b4f791eeaf245317fb4b6e07c45d741.svg)

![{\displaystyle [X,Y]}](https://img.franco.wiki/i/94470b44d283fde62130212956058ca6b727da37.svg)





![{\displaystyle [x]={\begin{bmatrix}x_{1}\\x_{2}\\x_{3}\end{bmatrix}}}](https://img.franco.wiki/i/74a95f1dd35d0a7eeadbe92f9cedc531e7b1a618.svg)
![{\displaystyle [\star x]={\begin{bmatrix}0&x_{3}&-x_{2}\\-x_{3}&0&x_{1}\\x_{2}&-x_{1}&0\\\end{bmatrix}}}](https://img.franco.wiki/i/f15c2cda48f59044bd5220e073233395cd0a4430.svg)
![{\displaystyle Q_{x}=[\star x]^{T}=-[\star x]}](https://img.franco.wiki/i/8807092389423885e00e21b2ff444971a710eda8.svg)
![{\displaystyle \quad [u\times v]=Q_{u}\ [v]}](https://img.franco.wiki/i/1b9662bbee20347362ab5818e5c1d30f6ab41fd5.svg)
![{\displaystyle \quad [u\wedge v]={\big [}\ [\star u],[\star v]\ {\big ]}=\left[Q_{u},Q_{v}\right]}](https://img.franco.wiki/i/41fa3c0afcdd0ebf390c2597635d021a5132b3bf.svg)

![{\displaystyle {\big ]}}](https://img.franco.wiki/i/31d63350d68291e3f56604a089e0e0b5a86c2472.svg)
























