Fonction nulle

En mathématiques, une fonction nulle est une fonction constante dont l'image est zéro. Elle possède de nombreuses propriétés et intervient dans de nombreux domaines des mathématiques. Elle est souvent utilisée comme exemple ou contre-exemple trivial.

Énoncé

On appelle généralement fonction nulle la fonction constante définie sur l'ensemble des nombres réels ou complexes par : ƒ(x) = 0. De manière plus rigoureuse, on dit qu'une fonction définie sur A sous-ensemble de ℂ, par exemple, est une fonction nulle (ou est la fonction nulle de A) si c'est la restriction à A de la fonction nulle précédente (autrement dit, si ∀ x ∈ A, ƒ(x) = 0 et si ƒ n'est pas définie en dehors de A).

Plus généralement, soient (E, +) un ensemble muni d'une opération ayant un élément neutre noté 0 (par exemple un groupe commutatif, un anneau, un espace vectoriel) et X un ensemble quelconque. L'application nulle est l'application ƒ de X dans E définie par ƒ(x) = 0 pour tout élément x de X.

Propriétés

Signe

C'est la seule fonction, qui, pour tout réel x, est à la fois négative et positive puisqu'elle est nulle.

Parité

Une des conséquences de son signe est qu'elle est la seule fonction définie sur ℝ ou sur ℂ à la fois paire et impaire, puisque pour tout réel x, on a ƒ(x) = ƒ(–x) = –ƒ(x) = 0. On remarquera que ce résultat ne s'étend pas au cas général : pour que la fonction nulle de A soit paire (et impaire), il faut que A soit « symétrique » par rapport à 0, c'est-à-dire que x ∈ A ⇒ –x ∈ A.

Opérations algébriques

Si X est un ensemble et (E, ∗) un ensemble ayant un élément neutre 0, alors la fonction nulle est l'élément neutre de l'espace E^X des applications de X dans E, muni de l'opération induite par l'opération ∗ de E.

En particulier, si (E, +, ⋅) est un espace vectoriel (ℝ ou ℂ munis de leurs lois usuelles par exemple), alors la somme d'une fonction ƒ et de la fonction nulle est la fonction ƒ et le produit de la fonction nulle par un scalaire est la fonction nulle.

Dérivée

La fonction nulle sur ℝ est l'unique solution de l'équation différentielle y' = y s'annulant en au moins un point.

Intégrale et primitives

L'intégrale de la fonction nulle est nulle sur tout intervalle inclus dans l'ensemble des réels ; les primitives de la fonction nulle (sur ℝ) sont donc les fonctions constantes.

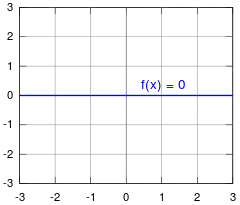
Représentation graphique

La représentation graphique de la fonction nulle sur ℝ est la droite d'équation y = 0 : c'est l'axe des abscisses.

Liens avec le polynôme nul

À tout polynôme à coefficients dans un anneau commutatif A est associée une fonction polynomiale de A dans A. La fonction associée au polynôme nul est la fonction nulle. Si l'anneau A est intègre et infini (par exemple si A est un corps infini, comme ℝ ou ℂ), alors la réciproque est vraie, c'est-à-dire qu'un polynôme est nul dès que sa fonction polynomiale associée l'est (ou même, dès qu'elle s'annule sur une partie infinie de A).

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.