Différence entre masse et poids
Dans l'usage courant, on parle souvent de poids pour désigner la masse d'un objet, bien qu'il s'agisse en fait de concepts et de quantités différents. Néanmoins, lorsque deux objets sont soumis à la même gravité (c'est-à-dire à la même intensité de champ gravitationnel), l'objet ayant plus de masse pèse toujours plus que l'autre.
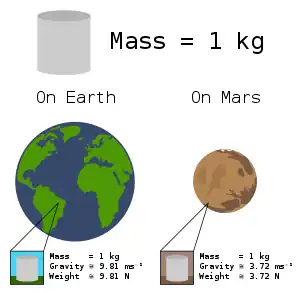
Du point de vue de la science, la masse est la quantité de « matière » contenue dans un objet (bien que la matière puisse être difficile à définir), alors que le poids est la force exercée sur la matière de l'objet par la gravité[1]. À la surface de la Terre, un objet dont la masse est d'un kilogramme pèse environ 9,81 newtons, ce qui correspond à la masse de l'objet multiplié par l'intensité du champ gravitationnel à l'endroit où se trouve l'objet. Le poids de l'objet est plus faible sur Mars, où la gravité est moins intense ; il est plus élevé sur Saturne, où la gravité est supérieure ; et il est très faible dans l'espace, loin de toute source importante de gravité. Mais dans tous les cas, l'objet a toujours la même masse.
Les objets matériels à la surface de la Terre ont tous un poids, bien qu'il soit parfois difficile de le mesurer. Un objet flottant librement sur l'eau, par exemple, ne semble pas avoir de poids puisqu'il est porté par l'eau. Mais s'il est ajouté à l'eau dans un récipient entièrement posé sur une balance, le poids total du récipient augmente. Ainsi, « l'objet en apesanteur » flottant dans l'eau transfère son poids au fond du récipient (où la pression augmente) et à la balance. De même, un ballon d'hélium a une masse mais il peut sembler n'avoir aucun poids, voire un poids négatif, en raison de sa flottabilité dans l'air. En fait, le poids du ballon et du gaz qu'il contient a tout simplement été transféré sur une grande partie de la surface de la Terre, ce qui rend sa mesure plus difficile. Le poids d'un avion en vol ne disparaît pas, il est également réparti sur la surface de la Terre. Lorsque l'avion est en vol, le poids qui est réparti sur le sol est le même que celui qu'avait l'avion lorsqu'il était posé sur la piste, sauf qu'il est réparti sur une plus grande surface.
Une définition scientifique plus rigoureuse de la masse est que celle-ci est une mesure de l'inertie d'un objet. L'inertie est la tendance qu'a un objet à ne pas changer son état de mouvement (à rester à vitesse constante) à moins d'être sollicité par une force externe non compensée. Le « poids » gravitationnel est la force créée lorsqu'une masse est soumise à un champ gravitationnel et que l'objet ne peut pas tomber librement, car il est soutenu ou ralenti par une contrainte mécanique, telle que la surface de la Terre. C'est cette force qui constitue le poids[2]. Cette force peut s'ajouter ou se soustraire à n'importe quel autre type de force qui agit sur l'objet.
Alors que le poids d'un objet varie proportionnellement à la force du champ gravitationnel, sa masse reste constante tant que l'on ne rajoute ni énergie, ni matière à l'objet[note 1]. Par exemple, bien qu'un satellite en orbite (qui est une forme particulière de chute libre) soit en « apesanteur », il conserve toujours sa masse et son inertie. Par conséquent, même en orbite, un astronaute essayant d'accélérer le satellite dans n'importe quelle direction doit toujours exercer une force. De plus, il devra exercer une force dix fois plus intense pour accélérer un satellite de 10 tonnes que pour accélérer un satellite d'une seule tonne s'il veut obtenir la même accélération pour les deux.
Aperçu

La masse est (entre autres choses) une propriété « inertielle », c'est-à-dire la tendance qu'a un objet à rester à vitesse constante tant qu'il n'est pas sollicité par une force extérieure. D'après les lois du mouvement d'Isaac Newton, qui datent de 1687[3], ainsi que de la formule importante issue de son travail : F = ma, un objet ayant une masse m d'un kilogramme, subit une accélération a d'un mètre par seconde par seconde (environ un dixième de l'accélération due à la gravité terrestre[note 2]), lorsqu'il est soumis à une force F d'un newton.
On peut observer l'inertie lorsqu'une boule de bowling est lancée horizontalement sur une surface plane et lisse, et qu'elle poursuit son mouvement horizontal. Ceci est tout à fait distinct du poids de la boule, qui est la force gravitationnelle vers le bas que l'on doit compenser si l'on veut maintenir la boule au-dessus du sol sans qu'elle ne le touche. Le poids de la boule de bowling sur la Lune serait le sixième de celui qu'il est sur Terre, bien que sa masse soit la même. Par conséquent, chaque fois que la physique de la cinétique des chocs (masse, vitesse, inertie, collisions élastiques et collision inélastiques) domine et que l'influence de la gravité est un facteur négligeable, le comportement des objets reste identique, même lorsque la gravité n'est pas la même. Par exemple, des boules de billard se disperseraient et reculeraient avec les mêmes vitesses et les mêmes énergies lors de la casse du début de la partie, que cette dernière se déroule sur la Lune ou sur Terre. En revanche, elles tomberaient beaucoup plus lentement dans les poches de la table.
En sciences physiques, les termes « masse » et « poids » ont été définis de manière rigoureuse comme des mesures distinctes car ce sont des propriétés physiques différentes. Mais dans l'usage quotidien, puisque tous les objets courants ont à la fois une masse et un poids et qu'ils sont presque proportionnels, le « poids » sert souvent à décrire les deux propriétés, sa signification étant sous-entendue selon le contexte. Par exemple, dans le commerce du détail, le « poids net » des produits fait en réalité référence à leur masse et est d'ailleurs exprimé en unités de masse telles que le gramme, les kilogramme, l'once ou la livre. À l'inverse, l'indice de charge d'un pneu automobile, qui précise la charge structurelle maximale qu'un pneu peut supporter, est indiqué en kilogrammes alors qu'il fait référence au poids maximal, c'est-à-dire à la force due à la gravité. Avant la fin du XXe siècle, la distinction entre les deux n'était pas strictement appliquée dans les documentations techniques de sorte que l'on trouve encore des expressions telles que « poids moléculaire », au lieu de « masse moléculaire ».
Parce que la masse et le poids sont des quantités distinctes, ils ont des unités de mesure différentes. Dans le système international d'unités (SI)[4] - [5], l'unité de masse est le kilogramme et l'unité de force (et par conséquent celle du poids) est le newton. Le kilogramme-force, qui n'appartient pas au SI, est également une unité de force généralement utilisée dans la mesure des poids. Il représente la force exercée par la gravité sur une masse d'un kilogramme, à la surface de la Terre. De même, la livre avoirdupois, utilisée à la fois dans le système impérial et dans les unités usuelles américaines, est une unité de masse et son unité de force associée est la livre-force.
Conversion entre unités de masse et de forces sur Terre
Lorsque le poids d'un objet (sa force gravitationnelle) est exprimé en « kilogrammes », il s'agit en fait du kilogramme-force (kgf ou kg-f), également connu sous le nom de kilopond (kp) dans les pays anglo-saxons, qui est une unité de force non SI. Tous les objets à la surface de la Terre sont soumis à une accélération gravitationnelle (de symbole g) d'environ 9,8 m/s2. La conférence générale des poids et mesures[6] - [7] - [8] a fixé la valeur de l'accélération normale de la pesanteur terrestre à exactement 9,806 65 m/s2 afin que des disciplines telles que la métrologie aient une valeur standard leur permettant de convertir des unités de masses en unités de forces et de pressions. Ainsi, le kilogramme-force est défini comme étant exactement 9,806 65 newtons. En réalité, l'accélération gravitationnelle varie légèrement en fonction de la latitude, de l'altitude et de la densité du sol. Ces variations sont généralement de quelques dixièmes de pour cent.
Pour les ingénieurs et les scientifiques, la distinction entre masse, force et poids est importante. Les ingénieurs dans les disciplines impliquant une charge pondérale (une force s'appliquant sur une structure du fait de la gravité), comme l'ingénierie des structures, convertissent la masse d'objets comme le béton et les automobiles, exprimée en kilogrammes, en une force, exprimée en newtons, en multipliant par un facteur d'environ 9,8 (deux chiffres significatifs sont généralement suffisants pour de tels calculs) pour déduire la charge de l'objet. Les propriétés des matériaux comme le module d'élasticité sont mesurées et publiées en termes de newton et de pascal (l'unité de pression SI).
Flottabilité et poids


Habituellement, la relation entre la masse et le poids sur Terre est hautement proportionnelle. Les objets qui sont cent fois plus massifs qu'une bouteille de limonade d'un litre pèsent presque toujours cent fois plus (environ 1000 newtons), ce qui est le poids auquel on pourrait s'attendre sur Terre pour un objet dont la masse est légèrement supérieure à 100 kilogrammes. Pourtant, ce n'est pas toujours le cas et il y a des objets familiers qui violent la proportionnalité entre masse et poids.
Un ballon gonflable rempli d'hélium est un objet familier pour beaucoup. Lorsqu'un tel ballon est entièrement rempli d'hélium, il a une certaine flottabilité, c'est-à-dire une force qui s'oppose à la gravité et qui le fait monter. Lorsque le ballon est partiellement dégonflé, il devient neutre et peut flotter dans la maison à un mètre ou deux du sol. Dans un tel état, il y a des moments où le ballon reste à la même hauteur, sans monter, ni descendre. Si le ballon est alors placé au-dessus d'une balance, aucune force ne s'y applique, le ballon n'a aucun poids et se trouve, dans un sens, en apesanteur. (En fait, comme indiqué plus loin, le poids a simplement été redistribué sur toute la surface de la Terre de sorte qu'il ne peut pas être mesuré.) S'il est vrai que la masse du caoutchouc formant le ballon ne fait que quelques grammes, ce qui pourrait être presque imperceptible, il conserve toujours cette masse, même lorsqu'il est gonflé et qu'il n'a plus de poids.
Contrairement à l'effet que les environnements à faible gravité ont sur le poids, la flottabilité ne fait pas disparaître le poids d'un objet. Le poids manquant est en réalité supporté par le sol, ce qui laisse moins de force (moins de poids) appliquée sur la balance théorique placée sous l'objet en question (bien que l'on puisse avoir quelques problèmes avec les aspects pratiques pour réaliser la pesée précise d'un objet individuel dans cette situation). Si l'on devait cependant peser une petite piscine remplie d'eau dans laquelle quelqu'un entrerait et commencerait à flotter, on constaterait que tout le poids de la personne est supporté par la piscine et, finalement, par la balance placée sous la piscine. Alors qu'un objet flottant, posé sur une balance fonctionnant correctement pour peser des objets flottants, pèserait moins, la masse de l'ensemble objet/fluide augmente de la valeur de la masse de l'objet une fois qu'il a été ajouté. L'air étant un fluide, ce principe s'applique également aux systèmes objet/air : le poids que l'objet perd grâce à la flottabilité dans l'air est supporté par un grand volume d'air entourant l'objet, ainsi que par le sol supportant l'air.
Les effets de la flottabilité n'affectent pas seulement les ballons. En sciences physiques, les liquides et les gaz sont des fluides, et lorsque les objets de taille macroscopique plus grand que les particules de poussière sont immergés dans un fluide sur Terre, ils ont un certain degré de flottabilité[note 3]. Dans le cas d'un nageur flottant dans une piscine ou d'un ballon flottant dans l'air, la flottabilité peut complètement compenser le poids gravitationnel de l'objet. Cependant, comme indiqué ci-dessus, un objet en suspension dans un fluide n'est fondamentalement pas différent d'un objet supporté par une élingue ou par un câble, le poids a simplement été transféré à un autre endroit, il n'a pas disparu.
La masse des ballons en « apesanteur » (donc de flottabilité neutre) peut être mieux appréciée avec des objets beaucoup plus gros tels que les montgolfières. Bien qu'il suffise d'un petit effort pour compenser leur poids lorsqu'elles se trouvent proche du vol stationnaire au-dessus du sol (elles peuvent souvent être à moins de cent newtons du poids zéro), l'inertie associée à leur masse de plusieurs centaines de kilogrammes, voire plus, peut facilement faire tomber un homme adulte lorsque la nacelle du ballon se déplace horizontalement au-dessus du sol.
La flottabilité des objets en cours de pesé, et la réduction de la force vers le bas qui en résulte, sous-tendent le principe d'Archimède, qui stipule que la force de flottabilité est égale au poids du fluide que l'objet déplace (remplace). Si ce fluide est de l'air, la force est faible et elle peut être négligée lorsque l'on pèse des objets beaucoup plus denses que l'air.
Effets de flottabilité dans l'air sur la mesure
L'effet de la flottabilité dans l'air sur les objets de la vie quotidienne est trop faible pour avoir une quelconque conséquence pour les activités de tous les jours. Par exemple, l'effet de diminution de la flottabilité sur le poids corporel (de densité relativement faible) est de 1⁄860 fois celle de la gravité (pour l'eau pure c'est environ 1⁄770 fois). Qui plus est, les variations de pression barométrique affectent rarement le poids d'une personne de plus de ±1⁄30 000[note 4]. Cependant, en métrologie (la science de la mesure), les étalons de masse de précision pour l'étalonnage des balances de laboratoire sont fabriqués avec une telle précision que la masse volumique de l'air doit être prise en compte pour compenser les effets de flottabilité. Compte tenu du coût des étalons de masse en platine-iridium, comme le prototype international du kilogramme (conservé en France et qui définissait la valeur du kilogramme avant 2019), des étalons de « travail » de haute qualité sont fabriqués à partir d'alliages spéciaux d'acier inoxydable[9] - [note 5]. Ils ont des masses volumiques d'environ 8000 kg/m3, et occupent un plus grand volume que ceux en platine-iridium, qui ont une masse volumique d'environ 21 550 kg/m3. Par commodité, une valeur standard de flottabilité par rapport à l'acier inoxydable a été développée pour les travaux de métrologie. Cette valeur se traduit par le terme de « masse conventionnelle »[10], qui est définie comme suit : « Pour un poids pris à la température de référence de 20 °C, la masse conventionnelle est la masse d’un poids de référence d’une masse volumique de 8000 kg/m3 qu’elle équilibre dans un air de masse volumique de 1,2 kg/m3 ». L'effet est faible, 150 ppm pour les étalons de masse en acier inoxydable, mais des corrections adéquates sont apportées lors de la fabrication de tous les étalons de masse de précision afin qu'ils aient la véritable masse étiquetée.
Chaque fois qu'une balance de laboratoire de haute précision est calibrée à l'aide d'un étalon en acier inoxydable, la balance est en fait calibrée à la masse conventionnelle, c'est-à-dire la masse réelle moins les 150 ppm de flottabilité. Étant donné que des objets de même masse ayant des densités différentes déplacent des volumes d'air différents (ils ont donc des flottabilités et des poids différents), la masse de l'objet mesurée par cette balance (par comparaison avec l'étalon de masse en acier inoxydable) est en réalité sa masse conventionnelle, c'est-à-dire sa masse réelle moins un degré inconnu de flottabilité. Pour des travaux de haute précision, le volume de l'objet doit être mesuré pour annuler mathématiquement l'effet de la flottabilité.
Types de balances et ce qu'elles mesurent


Quand on se tient debout sur une balance mécanique dans un cabinet médical, on mesure directement sa masse. En effet, les balances de type comparateurs de masses à « double plateau » comparent la force gravitationnelle exercée sur la personne se tenant sur la plate-forme avec celle exercée sur les contrepoids coulissants sur le fléau de la balance. La gravité est donc le mécanisme générateur de la force qui compense l'effet de la gravité sur votre propre masse et permet à l'aiguille de diverger de son point d'équilibre. Ces balances pourraient être placées à l'équateur terrestre ou aux pôles et donner exactement la même mesure, c'est-à-dire qu'elles n'indiqueraient pas faussement que le patient est 0,3 % plus lourd aux pôles qu'à l'équateur. Elles sont également immunisées contre la force centrifuge due à la rotation de la Terre autour de son axe et qui s'oppose à la gravité. Maintenant, si vous montez sur une balance à ressort ou sur une balance utilisant des capteurs de forces électroniques (les appareils à plateau unique), l'effet de la gravité sur votre masse est compensé par la force exercée par la résistance du ressort ou du capteur. Cette résistance ne dépend pas de la gravité. C'est donc votre poids (la force gravitationnelle) qui est mesuré par le ressort, et l'intensité du champ gravitationnel affectent la lecture. En pratique, lorsque de telles balances sont utilisées dans le commerce ou dans les hôpitaux, elles sont souvent ajustées sur place et certifiées sur cette base, afin que la masse qu'elles mesurent, exprimée en kilogrammes, soit au niveau de précision souhaité[11].
Articles connexes
Notes et références
Notes
- Voir l'article sur la masse au repos pour une discussion sur les différentes masses utilisées dans le contexte de la relativité restreinte. Il n'est pas nécessaire qu'un objet ou une particule se déplace à une vitesse proche de celle de la lumière c, pour que sa masse relativiste M (or γm) varie de manière mesurable par rapport à sa masse au repos m0. D'après les transformations de Lorentz et l'article d'Einstein de 1905 sur la théorie de la relativité restreinte, la masse relativiste est supérieure de 0,5 % à m0 à seulement 9,96 % de c, ce qui affecte les mesures effectuées avec une précision de 1 %. Alors que 10 % de la vitesse de la lumière peut sembler excessivement rapide dans la plupart des contextes, cela n'est pas suffisant pour être qualifié de « proche de la vitesse de la lumière ».
- En métrologie (la science des mesures), l'accélération de la pesanteur terrestre est considérée comme l'accélération normale de la pesanteur (symbole : gn), qui est définie comme étant exactement 9,806 65 mètres par seconde carrée (m/s2). L'expression « 1 m/s2 » signifie que pour chaque seconde qui s'écoule, la vitesse augmente d'un mètre par seconde supplémentaire. Une accélération de 1 m/s2 correspond à une variation de vitesse de 3,6 km/h par seconde.
- Les objets de la taille d'une petite particule de poussière, voire plus petits, sont si fortement influencés par le mouvement brownien qu'ils ne sont plus influencés par la flottabilité.
- Hypothèses : une densité de l'air de 1160 g/m3, une densité moyenne du corps humain (poumons complètement comprimés) égale à celle de l'eau, et des variations de la pression barométrique dépassant rarement ±22 mmHg (2,9 kPa). Hypothèses principalement variables : une altitude de 194 mètres au-dessus du niveau de la mer (l'altitude médiane des habitations humaines dans le monde), une température intérieure de 23 °C, un point de rosée de 9 °C et une pression barométrique de 760 mmHg (101 kPa), corrigée du niveau de la mer.
- Par exemple, pour le ré-étalonnage du prototype national du kilogramme américain en 1985, deux spécimens en acier inoxydable austénitique ont été utilisés à des fins de comparaison. L'un, appelé D2, était similaire à l'acier inoxydable 18-8 (AISI 304) (c'est-à-dire 18 % de chrome, 8 % de nickel). L'autre, appelé CH-1, était un alliage plus complexe qui pouvait être grossièrement désigné comme CrNiMo30-25-2 (composition chimique : 29,9 % de Cr, 25,1 % de Ni, 2,2 % de Mo, 1,45 % de Mn, 0,53 Si, 0,2 % de Cu, 0,07 % de C, 0,0019 % de P).
Références
- de Silva, G.M.S. (2002), Basic Metrology for ISO 9000 Certification, Butterworth-Heinemann
- National Physical Laboratory: What are the differences between mass, weight, force and load? (FAQ – Mass & Density)
- (la) Isaac Newton, Philosophiae Naturalis Principia Mathematica, Londres, [Joseph Streater, Samuel Smith] Imprimatur Samuel Pepys, Regalis Societas praeses. Julii 5. 1686. Jussu Societatis Regiae ac Typis Josephi Streater. Prostat Venales apud Sam. Smith ad insigna Principis Walliae in Coemiterio D. Pauli, aliosq, nonnullos Bibliopolas, , 510 p.
- Bureau international des poids et mesures (Convention du mètre signée à Paris le ), Documents diplomatiques de la conférence du mètre : 1er séance du sous la présidence du duc Decazes, Paris, Imprimerie nationale, , 135 p., 21 cm (lire en ligne [PDF]).
- Céline Fellag Ariouet, « Le système international d'unités », dans La science au présent, 2020, s,
- 3e CGPM, Paris, 1901, CR 70.
- Yaroslav Pigenet, « Ces constantes qui donnent la mesure », CNRS Le journal, (lire en ligne, consulté le ).
- Mathieu Grousson, « Mesures : le grand renversement », sur CNRS, (consulté le ).
- R. N. Davis, « Recalibration of the US National Prototype Kilogram », US Government Printing Office, Washington, vol. 90, no 4, , p. 267 (PMID 34566154, PMCID 6664201, DOI 10.6028/jres.090.015
 )
) - International Recommendation OIML R33, International Organization of Legal Metrology.
- National General Conference on Weights and Measures, Specifications, Tolerances, and Other Technical Requirements for Weighing and Measuring Devices, NIST Handbook 44