Désintégration du neutron libre

La désintégration du neutron libre (n) en un proton (p), un électron (e⁻) et un antineutrino électronique (ν̅_e) est un processus qui conserve à la fois la charge électrique et la projection de son spin sur un axe quelconque[2]. La conservation de la charge et du nombre leptonique, requise par l’interaction faible, explique la présence de l’électron et de l’antineutrino électronique[3]. Elle s’écrit[4] :

n → p + e⁻ + ν̅_e

Cette désintégration est rendue possible par le fait que l’énergie de masse du neutron est supérieure à la somme de celle du proton, de l’électron et de l’antineutrino électronique d’environ 0,782 MeV. Il décroit donc et l’excès de masse est converti en énergie cinétique qui se répartit entre les particules issues de la désintégration[3]. Ce processus peut également avoir lieu lorsque le neutron est lié à l’intérieur d’un noyau atomique : elle se produit lorsque le noyau est instable vis-à-vis d’une décroissance β⁻ ce qui le conduit à regagner davantage de stabilité[3].

Distribution en énergie de l’électron issu de la désintégration du neutron mesurée expérimentalement (points bleus) et le calcul théorique (ligne rouge).

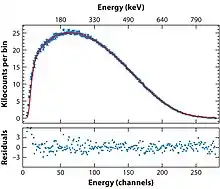
L’énergie de désintégration (basée sur les masses du neutron, du proton et de l’électron fournies par le CODATA 2014[5]) est égale à 0,782 333 05 MeV. Cette valeur est en accord avec l’énergie maximale de l’électron produit lors de la désintégration qui a été mesurée à 0,782 ± 0,013 MeV[6]. Cette dernière valeur n’est pas assez précise pour déterminer la masse au repos de l’antineutrino (qui doit en théorie être soustraite de l’énergie cinétique maximale de l’électron) ; celle-ci est contrainte par d’autres méthodes[7]. Par ailleurs, l’énergie cinétique maximale du proton est 751 eV[8].

Fondamentalement, le proton et le neutron sont tous deux composés de trois quarks de valence. Le neutron porte deux quarks d (chacun de charge -⅓ e) et un quark u (de charge +⅔ e), tandis que le proton est composé de deux quarks u et d’un quark d. L’un des quarks d du neutron se transforme en un quark u, conduisant à la formation d’un proton, avec l’émission d’un boson vectoriel massif W⁻, qui se désintègre ensuite en un électron et un antineutrino électronique[9], ce qui s’écrit :

d → u + e⁻ + ν̅_e

Une petite fraction des neutrons libres (de l’ordre de 9,2 ± 0,7 pour 1000 pour des photons émis ayant une énergie comprise entre 0,4 et 782 keV[4]) se désintègre en les mêmes produits que la désintégration β, mais avec une particule supplémentaire qui prend la forme d’un photon gamma (γ)[4] :

n → p + e⁻ + ν̅_e + γ

Ce photon gamma peut être compris comme une sorte de « bremsstrahlung interne » qui a lieu lorsque la particule bêta émise interagit électromagnétiquement avec la charge du proton[10].

Une portion encore plus faible de décroissance (environ quatre par million d’après des calculs théoriques[11] - [12]) est appelée « désintégration à deux corps » ou « désintégration β liée ». Prédite en 1947 par Raymond Daudel, Maurice Jean et Marcel Lecoin[13], cette désintégration n’avait encore jamais été observée en 2022. Expérimentalement, la probabilité d’une telle décroissance est inférieure à 2,7 × 10⁻³[4].

Un proton, un électron et un antineutrino électronique sont produits comme dans la désintégration β mais l’électron a une énergie cinétique inférieure à 13,6 eV ce qui l’empêche de s’échapper du proton et ainsi lui reste-t-il lié, formant un atome neutre d’hydrogène (l’un des « deux corps »). La théorie prévoit que l’atome d’hydrogène soit créé dans un état atomique sans moment angulaire, avec les probabilités de population de chaque état « s » suivantes : 83,2 % pour l’état « 1s », 10,4 % pour l’état « 2s », et le reste pour les niveaux supérieurs[12]. L’antineutrino électronique (l’un des « deux corps ») emporte la quasi-totalité de l’énergie de décroissance du neutron ; l’atome d’hydrogène (l’autre « corps ») n'est créé qu’avec une énergie cinétique de 325,7 eV[12]. Ce qui donne[4] :

n → ¹H + ν̅_e

Des expériences sont envisagées afin de mesurer cette désintégration en vue de tester la structure vecteur axiale de l’interaction faible[12].

Un autre type de désintégration du neutron est envisagé et étudié. Il s’agit d’une désintégration violant la conservation de la charge électrique[4] :

n → p + ν_e + ν̅_e

En 2022, aucune désintégration de ce type n’a jamais été observée. Si ce phénomène existe, il a une probabilité de se produire inférieure à 8 × 10⁻²⁷ (niveau de confiance de 68 %) sur l’ensemble des désintégrations du neutron libre[4].

Afin de pouvoir expliquer les durées de vie moyennes contradictoires (voir la section Contradiction entre les mesures par la technique de la bouteille et par temps de vol) mesurés par la technique du temps de vol et par la technique du stockage, les physiciens théoriciens Bartosz Fornal et Benjamín Grinstein ont calculé que la décroissance d’un neutron en une particule de matière noire, ${\displaystyle \chi }$, accompagnée d’un électron et d’un positron avec un rapport d’embranchement de l’ordre de 1 % permettrait d’expliquer la contradiction des résultats expérimentaux[14].

${\displaystyle n\rightarrow \chi +e^{-}+e^{+}}$

Xuan Sun et son équipe ont tenté d’identifier les traces d’une telle décroissance dans leurs données expérimentales. L’étude a exclu que ce canal de décroissance soit responsable de l’écart observé entre les deux techniques expérimentales (pour la somme des énergies cinétiques de l’électron et du positron comprise entre 100 et 644 keV). Les auteurs ont également calculé que s’il existe d’autres canaux de décroissance mettant en jeu des particules de matière noire, la probabilité d’une telle décroissance est inférieure à 10⁻⁴ avec un niveau de confiance supérieur à 90 % (pour la même gamme en énergie cinétique)[15]. Michael Klopf et son équipe ont trouvé des résultats similaires en réétudiant les données d’une autre expérience[16].

Après la découverte du neutron par James Chadwick en 1932, son instabilité lorsqu'il n'est pas lié à un noyau atomique est supposée par James Chadwick et son étudiant en thèse Maurice Goldhaber en 1935[20] en partant de la constatation que le neutron est plus massif que le proton.

La mesure de la demi-vie du neutron n'a pas été possible avant la Seconde Guerre mondiale du fait du manque de sources intenses de neutrons[21]. Le besoin de plutonium dans le cadre du projet Manhattan a nécessité la construction du réacteur graphite X-10 au laboratoire national d'Oak Ridge en 1943. Après la guerre, le réacteur a été reconverti à des fins de recherche uniquement.

L'utilisation de la source de neutrons produits par ce réacteur a permis la première observation de la désintégration du neutron, rapportée en 1948 par Arthur H. Snell et Leonard C. Miller (décédé 4 mois avant la publication du rapport)[22]. Dans leur rapport, les auteurs ont uniquement observé la désintégration du neutron mais n'ont pas mesuré sa durée de vie. Ils se risquent néanmoins à une estimation de celle-ci et arrivent à une valeur comprise entre 15 et 27 minutes[22].

Article sur l'observation de la décroissance du neutron par Arthur Sneel et Frances Pleasonton dans le journal interne du laboratoire national d'Oak Ridge.

Les premières mesures de la demi-vie du neutron sont publiées en 1950 par Arthur H. Snell, Frances Pleasonton et R. V. McCord[23] d'un côté et John Michael Robson d'un autre côté[24]. Les deux expériences se basent sur la détection d'un des produits de désintégration du neutron ; les électrons pour l'équipe de Snell et les protons pour Robson. Arthur Snell et son équipe ont continué à utiliser le réacteur d'Oak Ridge tandis que John Robson a réalisé son expérience sur le réacteur des laboratoires nucléaires de Chalk River au Canada. La première équipe mesure une durée de vie comprise entre 10 et 30 minutes tandis que Robson mesure une demi-vie comprise entre 9 et 25 minutes.

La méthode de désintégration en vol consiste à mesurer le nombre de protons ou d’électrons issus de la désintégration des neutrons présents dans un faisceau. Cette méthode est utilisée pour la première fois en 1951 par John Michael Robson[17]. Le faisceau de neutrons est produit par un réacteur nucléaire. Afin de déterminer la densité de neutrons dans le faisceau, on utilise typiquement une feuille mince de matière avec laquelle les neutrons du faisceau interagissent[30].

Dans ce genre d’expériences, le temps de vie du neutron est obtenu via la relation[30] :

${\displaystyle \tau _{n}=\left({\frac {L}{\rho _{\text{feuille}}\sigma _{\text{th}}v_{\text{th}}}}\right)\left({\frac {R_{n}}{R_{p}}}\right)\left({\frac {\epsilon _{p}}{\epsilon _{n}}}\right)}$

• où L est la longueur du volume dans lequel les neutrons se désintègrent,
• ρ_feuille est la densité de la feuille (en atomes par m²),
• σ_th est la section efficace d’absorption de neutron thermique à la vitesse de référence v_th=2 200 m/s,
• R_n est le taux de comptage des neutrons,
• R_p est le taux de comptage des produits de décroissance des neutrons (protons ou électrons),
• et ε_n et ε_p sont respectivement l’efficacité de détection d’un neutron et de détection des produits de décroissance du neutron (proton ou électron).

Cette méthode utilise des neutrons ultra-froids qui sont stockés dans une bouteille pendant toute leur durée de vie. L’énergie cinétique des neutrons est si faible qu’ils se réfléchissent sur les parois de la bouteille conçue dans un matériau approprié. Si la bouteille est suffisamment haute verticalement alors les neutrons sont piégés par la gravité terrestre. On compte les neutrons que l’on a au début de l’expérience et on compte les neutrons qui n’ont pas été désintégrés à un temps donné. En principe, les neutrons restants sont comptés au bout de deux durées données Δt₁ et Δt₂ (avec la durée la plus longue d’une longueur comparable à la durée de vie du neutron), N₁ et N₂ respectivement. En considérant que les seules pertes de neutrons sont dues à la désintégration de ceux-ci, alors la durée de vie est déterminée par la relation suivante[31]

${\displaystyle \tau _{n}={\frac {\Delta t_{2}-\Delta t_{1}}{\ln(N_{1}/N_{2})}}}$

En pratique, la mesure est rendue plus compliquée du fait que les neutrons qui disparaissent ne le sont pas tous du fait de leur désintégration. Ils peuvent en effet être absorbés par les parois de la bouteille du fait d’impuretés du matériau, certains neutrons avec une énergie cinétique trop importante peuvent s’échapper de la bouteille. On utilise alors la relation suivante pour corriger la durée de vie du neutron des effets qui conduisent à la disparition de neutrons autrement que par désintégration[31] :

${\displaystyle {\frac {1}{\tau }}={\frac {1}{\tau _{n}}}+{\frac {1}{\tau _{\text{inelastique}}}}+{\frac {1}{\tau _{\text{capture}}}}+{\frac {1}{\tau _{\text{autre}}}}}$

où

• ${\displaystyle \tau }$ est la durée de vie des neutrons stockés ; celle que l’on mesure,
• ${\displaystyle \tau _{n}}$ est la durée de vie du neutron ; celle qui correspond à la désintégration du neutron par radioactivité β,
• ${\displaystyle \tau _{\text{inelastique}}}$ correspond aux pertes dues aux diffusions inélastiques sur les parois de la bouteille,
• ${\displaystyle \tau _{\text{capture}}}$ correspond aux pertes dues aux captures neutroniques par les parois et
• ${\displaystyle \tau _{\text{autre}}}$ correspond aux pertes attribuées à d’autres mécanismes tels que des interactions avec le gaz résiduel ou des trous de la bouteille qui permettent aux neutrons de s’échapper.

Cette méthode a été proposée pour la première fois en 1977 par Yu. Yu. Kosvintsev[32]. Il publie les résultats de la première expérience utilisant une bouteille en 1980[33]. Comparée à la méthode de désintégration en vol, cette méthode présente plusieurs avantages. D’une part, la mesure des taux de neutrons N₁ et N₂ sont des mesures relatives contrairement à la méthode de désintégration en vol qui nécessite une mesure absolue des taux de neutrons et des produits de décroissance. D’autre part, le bruit de fond de radiations est beaucoup plus faible dans une expérience utilisant une bouteille, car elle ne nécessite pas la présence d’un flux important de neutrons[34].

En 2022, la valeur de la durée de vie du neutron avec le minimum d’incertitude a été obtenue en utilisant cette technique[19] ce qui correspond à une incertitude totale (statistique et systématique) de 0,36 s[35].

Tout comme la méthode de la bouteille, la méthode du piégeage magnétique utilise des neutrons ultra-froids. Dans cette méthode, les neutrons sont confinés à l’intérieur d’un piège magnétique afin d’éviter les interactions des neutrons avec la matière responsable de la disparition de certains d’entre eux dans la méthode de la bouteille : capture, diffusion inélastique, etc. Ils sont piégés puis libérés au bout d’un certain temps pour être comptés. Les résultats de la première expérience utilisant un piège magnétique ont été publiés en 1978 par Klaus-Jürgen Kügler, Wolfgang Paul et Uwe Trinks[36].

Dans ce genre d’expérience, certains neutrons peuvent également être perdus du fait de leur dépolarisation, ce qui se traduit par un échappement du neutron du piège, ou si leur énergie mécanique est supérieure au potentiel maximum du piège mais dont la trajectoire est telle que le temps nécessaire pour s’échapper du piège est de l’ordre du temps de vie du neutron[37].

Connaissant la composition de l’atmosphère d’une planète et de sa surface, il est possible de modéliser le nombre de neutrons qui devraient être créés après spallation des atomes de l’atmosphère ou de la surface après collision avec des rayons cosmiques pour une gamme de durée de vie. Ces neutrons sont détectés par un spectromètre à neutrons installé sur une sonde spatiale en orbite[26]. Au niveau de la philosophie, cette méthode est une méthode de stockage. Jack Wilson, premier auteur de cette étude, indique ainsi : « c’est comme une expérience sur une grande bouteille, mais au lieu d’utiliser des murs et des champs magnétiques, nous utilisons la gravité de Vénus pour confiner les neutrons pendant des périodes comparables à leur durée de vie »[trad 1] - [38].

Cette méthode a été testée pour la première fois en 2020 à partir des données récupérées plusieurs années plus tôt par la sonde MESSENGER lors de ses orbites autour de Mercure ainsi que de son survol de Vénus[26]. Le résultat obtenu 780±60_stat±70_syst s est cohérent avec les autres valeurs proposées jusque-là[26]. En revanche, il n’est a priori pas possible d’égaler la précision des autres méthodes sans mission spatiale dédiée[26]. En 2021, ce type d’expérience a été réalisé avec les instruments de la mission Lunar Prospector ce qui a donné la valeur plus précise de 887±14(stat)⁺⁷₋₃(syst) s[39] - [40].

Mesures expérimentales utilisées par le Particle Data Group en 2018 et mesures plus récentes depuis pour l’évaluation du temps de vie moyen du neutron. Les données en rouge correspondent à des mesures utilisant la technique de la désintégration en vol tandis que les données en bleu désignent des expériences utilisant la technique du stockage. Les zones rouge et bleue sont centrées sur la valeur moyenne de la durée de vie moyenne du neutron pour les deux types d’expérience. La largeur de chaque zone correspond à un écart-type.

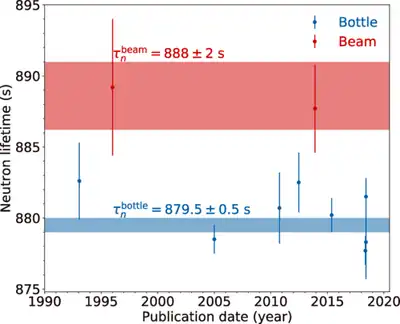
Une mesure est toujours accompagnée d’une incertitude. Cette incertitude a deux origines : statistique et systématique. L’incertitude statistique dépend uniquement de la taille de l’échantillon utilisé pour réaliser la mesure. Plus la taille de cet échantillon est grand, plus l’incertitude statistique est faible. L’incertitude systématique concerne toutes les sources qui pourraient conduire à une erreur de mesure. Elle est propre à la technique expérimentale et est, par nature, difficile à évaluer. L’utilisation de techniques expérimentales différentes – la désintégration en vol et le stockage – permet de s’assurer que l’ensemble des sources d’incertitudes systématiques ont correctement été prises en compte : les mesures effectuées avec une méthode ou l’autre doivent donner le même résultat.

Or, les mesures effectuées depuis les années 1990 par les deux types de mesures donnent des résultats divergents comme le montre la figure ci-contre. Les mesures utilisant la technique de la désintégration en vol donnent une valeur moyenne de la durée de vie moyenne du neutron de 888,0 ± 2,0 s tandis que les expériences utilisant la technique du stockage donnent en moyenne 879,6 ± 0,6 s[2]. Les résultats des mesures réalisées suivant les deux méthodes diffèrent donc d’environ 8 secondes, ce qui est bien supérieur aux incertitudes associées aux résultats de chacun des deux types de mesure. La probabilité d’obtenir une telle différence, du seul fait du hasard, est très faible[alpha 1] - [2].

Un tel écart peut traduire la non prise en compte d’un effet systématique dans l’une des deux méthodes, voire les deux. Par exemple, si le neutron peut se désintégrer en d’autres produits qu’un proton et un électron, la méthode de la désintégration en vol surestimera sa durée de vie, alors que les expériences de stockage ne seront pas impactées : la désintégration en vol ne se base que sur la détection du proton produit.

Ainsi deux théoriciens de l’université de Californie à San Diego ont-ils proposé en mai 2018 que le neutron puisse se désintégrer en une particule inconnue de matière noire et un photon gamma[41]. Cependant aucune trace expérimentale d’une telle désintégration n’a pu être observée[42]. D’autres modes de désintégrations sont possibles et n’ont pas été exclus par les observations expérimentales[43].

Il est également possible qu’un phénomène physique inconnu soit à l’origine de cet écart. Une explication faisant intervenir de la physique au-delà du modèle standard a été proposée par des théoriciens, tel que Zurab Berezhiani. Il a proposé avec ses collègues l’existence d’un hypothétique « neutron miroir » qui n’interagirait pas ou peu avec la matière ordinaire[44]. Une désintégration en ce neutron miroir se traduirait alors par une absence de détection dans les expériences de désintégration en vol[2].

Des théoriciens essaient de calculer la valeur de la durée de vie moyenne du neutron à partir de la chromodynamique quantique. En 2018, ces calculs donnent une valeur de 880 ± 14 s. L’importance de l’incertitude ne permet pas de départager les deux types de mesure[45].

Mesures expérimentales utilisées par le Particle Data Group comparées aux mesures de neutrons depuis l’espace (en gris).

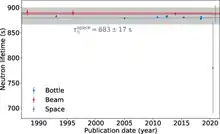
En 2020, la méthode basée sur le décompte depuis l’espace de neutrons émis par la surface ou l’atmosphère sous l’effet de spallation par les rayons cosmiques a donné des résultats encourageants, quoiqu’entâchés d’une incertitude élevée[26]. Avec une mission dédiée spécialement à cet objectif, il pourrait être possible de départager les résultats fournis par les deux autres classes de méthode[26].

Bien que la valeur la plus précise de l’élément de la matrice CKM |V_ud| soit obtenue à partir des transitions super-permises[46], de nombreuses expériences tentent d’apporter des contraintes sur cette valeur à partir de la mesure du temps de vie du neutron. La durée de vie moyenne du neutron, ${\displaystyle \tau _{n}}$, est reliée à la valeur de cet élément de matrice via la relation[47] :

${\displaystyle |V_{ud}|^{2}={\frac {5024,7\ {\text{s}}}{\tau _{n}(1+3g_{A}^{2})(1+\Delta _{R}^{V})}}}$

où ${\displaystyle g_{A}\equiv {\frac {G_{A}}{G_{V}}}}$, soit le rapport de la constante de couplage vecteur axiale G_A sur la constante de couplage vectorielle G_V et ${\displaystyle \Delta _{R}^{V}}$ représente les corrections radiatives électrofaibles internes.

La seule mesure de la durée de vie moyenne du neutron ne permet pas de déterminer la valeur de l’élément de matrice puisqu’il faut également connaître la valeur de g_A. Cette dernière est déterminée à partir d’une autre observable mesurée lors de la désintégration du neutron comme l’asymétrie A.

Cette asymétrie correspond au fait que lors de la désintégration de neutrons polarisés, l’émission des électrons est asymétrique par rapport au plan perpendiculaire à la direction du spin des neutrons. Le coefficient d’asymétrie A suit la relation (si on suppose une interaction vecteur axiale)[48] :

${\displaystyle W(\theta )=1+A\cos(\theta ){\frac {v_{e}}{c}}}$,

où W représente l’asymétrie, v_e la vitesse de l’électron, c la vitesse de la lumière dans le vide et θ l’angle entre la direction d’émission de l’électron et la direction du spin du neutron.

Par ailleurs, le coefficient A est relié à g_A par la relation suivante[49] :

${\displaystyle A=-2g_{A}{\frac {g_{A}-1}{1+3g_{A}^{2}}}}$

Principales réactions nucléaires se produisant lors de la nucléosynthèse primordiale.

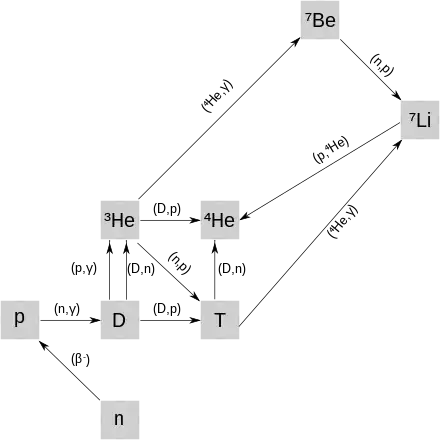
Le modèle de la nucléosynthèse primordiale permet d’expliquer la formation et l’abondance des éléments légers (de l’hydrogène jusqu’au béryllium). Elle débute environ 3 minutes après le Big Bang[50]. Différentes réactions nucléaires impliquant les protons et les neutrons, jusqu’à présent libres, permettent de produire ces noyaux. La réaction p + n → D + γ démarre et d’autres réactions à base de deutérium conduisent principalement à la formation d’hélium mais également, en moindres proportions, de lithium[51] (voir la figure ci-contre). La durée de vie du neutron joue un rôle important dans la modélisation de ces réactions étant donné qu’elle influe directement sur le nombre de neutrons disponibles pour les réactions (plus précisément elle influe sur le rapport entre le nombre de protons et le nombre de neutrons). Ainsi la précision sur la valeur de la durée de vie du neutron était-elle, en 1999[52], le principal facteur limitant une estimation plus précise de la quantité d’hélium 4 produite lors de la nucléosynthèse primordiale.

En effet, une durée de vie du neutron trop courte aurait conduit à la quasi-disparition de ceux-ci avant que les réactions nucléaires conduisant à la production de noyaux n’aient pu débuter tandis qu’une durée de vie plus longue aurait conduit à une surabondance des noyaux d’hélium, ce qui aurait alors perturbé la formation d’éléments plus lourds[2]. Une connaissance précise de la durée de vie du neutron permet de vérifier que le modèle de la nucléosynthèse primordiale reproduit certaines des observations astrophysiques liées à cette durée de vie et si des désaccords sont observés, une révision de ce modèle devra être envisagée[2].

• (en) R.L. Workman et al., « Review of Particle Physics », Progress of Theoretical and Experimental Physics, vol. 2022, n^o 8,‎ août 2022 (DOI 10.1093/ptep/ptac097, lire en ligne [PDF])
• Pascal Grivot, Mesure de la durée de vie du neutron libre par la détection des électrons de désintégration au moyen d’une chambre à migration, Université scientifique technologique et médicale de Grenoble, 26 janvier 1988 (lire en ligne [PDF]) (thèse de physique nucléaire)