Courbe d'intersection
En géométrie, une courbe d'intersection est une courbe commune à deux objets géométriques. Dans le cas le plus simple, l'intersection de deux plans non parallèles dans l'espace euclidien est une droite. En général, une courbe d'intersection est constituée des points communs à deux surfaces qui se croisent transversalement, ce qui signifie qu'en tout point commun les normales à la surface ne sont pas colinéaires. Cette restriction exclut les cas où les surfaces se touchent ou ont des parties de surface communes.
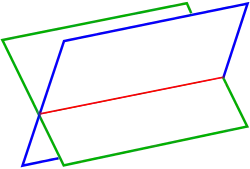
La détermination analytique de la courbe d'intersection de deux surfaces n'est aisée que dans des cas simples ; par exemple :
- l'intersection de deux plans
- la section plane d'une quadrique (sphère, cylindre, cône, etc.)
- l'intersection de deux quadriques dans des cas particuliers.
Pour le cas général, la littérature fournit des algorithmes de calcul des points d'intersection de deux surfaces[1].
Droite d'intersection de deux plans
Soient deux plans linéairement indépendants, c'est-à-dire que les plans ne sont pas parallèles.
On recherche une représentation paramétrique de la droite d'intersection.
Un vecteur directeur de la droite peut être obtenu à partir du produit vectoriel des vecteurs normaux : .
Un point de la droite d'intersection peut être déterminé en coupant les plans donnés avec le plan, qui est orthogonal à et . En injectant la représentation paramétrique de dans les équations de et on obtient les paramètres et .
- Exemple
- on cherche la droite , intersection de
Les vecteurs normaux sont et la direction de la droite d'intersection est donc . Pour le point , on obtient de la formule ci-dessus Ainsi
est une représentation paramétrique de la droite d'intersection.
- Remarques :
- Dans des cas particuliers, la détermination de la droite d'intersection par le pivot de Gauss peut être plus rapide.
- Si l'un (ou les deux) des plans est donné par sa représentation paramétrique telle que , on obtient comme vecteur normal et l'équation est : .
Courbe d'intersection d'un plan et d'une quadrique
Dans tous les cas, la courbe d'intersection d'un plan et d'une quadrique (sphère, cylindre, cône...) est une conique[2]. Une application importante des sections planes de quadriques est les lignes de contour de quadriques. Dans tous les cas (projection parallèle ou centrale), les courbes de niveau des quadriques sont des sections coniques.
Courbe d'intersection d'un cylindre ou d'un cône et d'une quadrique
Il est facile de déterminer les points d'intersection d'une droite avec une quadrique (c'est-à-dire une intersection droite-sphère) ; il suffit de résoudre une équation quadratique. Ainsi, toute courbe d'intersection d'un cône ou d'un cylindre (qui sont deux surfaces réglées) avec une quadrique est constituée des points d'intersection des droites et de la quadrique.
Les images montrent les possibilités qui se présentent lors de l'intersection d'un cylindre et d'une sphère :
- la courbe a une seule boucle
- la courbe a deux boucles non sécantes
- la sphère et le cylindre se touchent en un point singulier. La courbe d'intersection est auto-sécante. La courbe est alors une fenêtre de Viviani
- si le cylindre et la sphère ont le même rayon et que le milieu de la sphère est situé sur l'axe du cylindre, alors la courbe d'intersection se compose uniquement de points singuliers (formant un cercle). Cette définition peut servir à définir le contour apparent de la sphère.
 Intersection d'une sphère et d'un cylindre à une boucle
Intersection d'une sphère et d'un cylindre à une boucle Intersection d'une sphère et d'un cylindre à deux boucles
Intersection d'une sphère et d'un cylindre à deux boucles
 Intersection d'une sphère et d'un cylindre avec un point singulier
Intersection d'une sphère et d'un cylindre avec un point singulier Intersection d'une sphère et d'un cylindre de même rayon
Intersection d'une sphère et d'un cylindre de même rayon
Cas général : méthode de marche
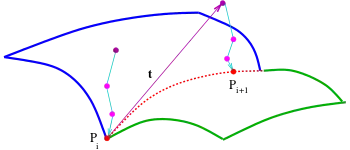
En général, il n'y a pas de fonctionnalités particulières à exploiter. Une possibilité pour déterminer un polygone de points de la courbe d'intersection de deux surfaces est la méthode de marche. Il se compose de deux parties essentielles[1]:
- La première partie est l'algorithme de point de courbe, qui détermine à partir d'un point de départ au voisinage des deux surfaces un point sur la courbe d'intersection. L'algorithme dépend essentiellement de la représentation des surfaces données. La situation la plus simple est celle où les deux surfaces sont implicitement données par des équations , car les fonctions fournissent des informations sur les distances aux surfaces et indiquent via les gradients le chemin vers les surfaces. Si une ou les deux surfaces sont données par leurs représentations paramétriques, les avantages du cas implicite n'existent pas. Dans ce cas, l'algorithme de point de courbe utilise des procédures chronophages comme la détermination du point de pied d'une perpendiculaire sur une surface.
- La deuxième partie de la méthode de marche commence par un premier point sur la courbe d'intersection, détermine la direction de la courbe d'intersection à l'aide des normales de surface, puis fait un pas avec une longueur de pas donnée dans la direction de la ligne tangente, afin d'obtenir un point de départ pour un deuxième point de courbe...
L'algorithme de marche produit pour tout point de départ un polygone sur la courbe d'intersection. Si la courbe d'intersection se compose de deux parties, l'algorithme doit être exécuté en utilisant un deuxième point de départ pratique. L'algorithme est assez robuste. Habituellement, les points singuliers ne posent aucun problème, car la chance de rencontrer exactement un point singulier est très faible (voir image : intersection d'un cylindre et de la surface ).
 Intersection de la surface d'équation avec un cylindre : cas de deux boucles disjointes
Intersection de la surface d'équation avec un cylindre : cas de deux boucles disjointes Intersection de la surface d'équation avec un cylindre : cas à une boucle
Intersection de la surface d'équation avec un cylindre : cas à une boucle Intersection de la surface d'équation avec un cylindre : cas avec un point singulier
Intersection de la surface d'équation avec un cylindre : cas avec un point singulier
Application : ligne de contour
Un point de la courbe de niveau d'une surface implicite d'équation et projection parallèle de direction doit remplir la condition , parce que doit être un vecteur tangent, ce qui signifie que tout point de contour est un point de la courbe d'intersection des deux surfaces implicites
- .
Pour les quadriques, est toujours une fonction linéaire. Ainsi la courbe de niveau d'une quadrique est toujours une section plane (c'est-à-dire une section conique).
La courbe de niveau de la surface (voir photo) a été tracé par la méthode de la marche.
- Remarque
- La détermination d'un polygone de contour d'une surface paramétrique nécessite de tracer une courbe implicite dans le plan des paramètres[3].
- Condition pour les points de contour : .
Courbe d'intersection de deux polyèdres
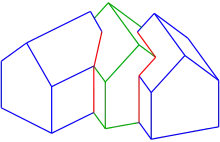
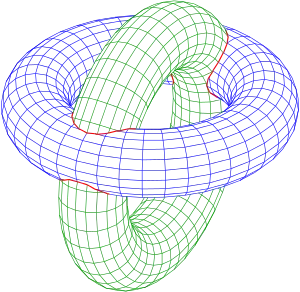
La courbe d'intersection de deux polyèdres est un polygone (voir intersection de trois maisons). L'affichage d'une surface définie paramétriquement se fait généralement en cartographiant un réseau rectangulaire dans l'espace. Les quadrilatères spatiaux sont presque plats. Ainsi, pour l'intersection de deux surfaces définies paramétriquement, l'algorithme d'intersection de deux polyèdres peut être utilisé[4].
Articles connexes
- Théorie des intersections
- Exemples de courbes d'intersection
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Intersection curve » (voir la liste des auteurs).
- (en) Geometry and Algorithms for COMPUTER AIDED DESIGN, p. 94
- (de) CDKG: Computerunterstützte Darstellende und Konstruktive Geometrie (TU Darmstadt) (PDF; 3,4 MB), p. 87–124
- (en) Geometry and Algorithms for COMPUTER AIDED DESIGN, p. 99
- (en) Geometry and Algorithms for COMPUTER AIDED DESIGN p. 76
Bibliographie
- (en) C. L. Bajaj, C. M. Hoffmann et R.E. Lynch, « Tracing surface intersections », Computer Aided Geometric Design, vol. 5, no 4, , p. 285-307 (DOI 10.1016/0167-8396(88)90010-6).
- (en) R. E. Barnhill et S. N. Kersey, « A marching method for parametric surface/surface intersection », Computer Aided Geometric Design, vol. 7, nos 1-4, , p. 257-280 (DOI 10.1016/0167-8396(90)90035-P).
- (en) R. Barnhill, G. Farin, M. Jordan et B. Piper, « Surface/Surface intersection », Computer Aided Geometric Design, vol. 4, nos 1-2, , p. p 3-16 (DOI 10.1016/0167-8396(87)90020-3).
- (en) Changhe Tu, Wenping Wang et Jiaye Wang, « Classifying the nonsingular intersection curve of two quadric surfaces », Geometric Modeling and Processing. Theory and Applications. GMP 2002. Proceedings, Wako, Japan, , p. 23-32 (DOI 10.1109/GMAP.2002.1027493).
Liens externes
- COURBE ALGÉBRIQUE 3D sur MathCurve































