Perpendicularité

Le segment PQ en bleu est perpendiculaire au segment AB :
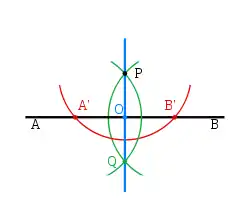
1. prendre un compas,
2. piquer la pointe sèche du compas sur P et tracer l'arc de cercle en rouge (le rayon du cercle en rouge est un peu plus grand que la distance du point P au segment AB).
3. En gardant la même ouverture au compas, piquer la pointe sèche du compas sur A' et tracer l'arc de cercle en vert.
4. Toujours en gardant la même ouverture au compas, piquer la pointe sèche sur B' et tracer l'arc de cercle en vert.
5. Les deux arcs en vert se rencontrent au points Q et P.
6. Prendre une règle.
7. Tracer le segment PQ.

En géométrie euclidienne plane, deux droites non parallèles sont toujours sécantes. Lorsqu'elles se coupent en formant un angle droit (i.e. quatre angles droits), elles sont dites perpendiculaires. Les directions des droites étant orthogonales, les droites sont dites aussi orthogonales. En revanche, deux segments peuvent avoir des directions orthogonales sans pour autant se couper. Ce n'est que si les segments se coupent en angle droit qu'ils seront dits perpendiculaires.

Dans le plan, par un point donné, ne passe qu'une seule droite perpendiculaire à une droite donnée.

Dans le plan, les notions de droites perpendiculaires et parallèles sont liées par les propriétés suivantes :

• Si deux droites sont perpendiculaires, toute droite parallèle à l'une est perpendiculaire à l'autre.
• Si deux droites sont parallèles, toute droite perpendiculaire à l'une est perpendiculaire à l'autre.
• Si deux droites sont perpendiculaires à une même droite alors elles sont parallèles entre elles.

Droites perpendiculaires : le produit de leur pente (ou taux de variation) est égal à -1.

la condition /u+v/=/u-v/ correspond à: u et v sont perpendiculaires

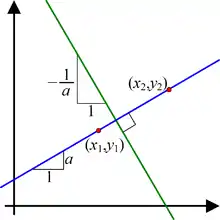
Si le plan est muni d'un repère orthonormal [on peut[1], supposant acquis le théorème de Pythagore, via la condition évoquée ci-contre dans l'illustration, retrouver la condition classique (ac+bd=0) pour que deux Vecteurs u(a,b) et v(c,d) soient perpendiculaires (on dit[1] aussi orthogonaux)], et si les droites sont définies par les équations ${\displaystyle y=ax+b}$ et ${\displaystyle y=a'x+b'}$, les droites sont perpendiculaires si et seulement si le produit de leurs coefficients directeurs aa' est égal à -1.

Si le plan est muni d'un repère orthonormal et si les droites sont définies par les équations ${\displaystyle ax+by+c=0}$ et ${\displaystyle a'x+b'y+c'=0}$, les droites sont perpendiculaires si et seulement si ${\displaystyle aa'+bb'=0}$.

On note la perpendicularité avec le symbole ${\displaystyle \perp }$; ainsi, ${\displaystyle PQ\perp AB}$ indique que les segment PQ est perpendiculaire au segment AB.

Dans un espace euclidien, deux sous-espaces vectoriels ${\displaystyle F_{1}}$ et ${\displaystyle F_{2}}$ sont dits orthogonaux quand tout vecteur de l'un est orthogonal à tout vecteur de l'autre, c'est-à-dire quand ${\displaystyle F_{1}\subset F_{2}^{\bot }}$ (qui équivaut encore à ${\displaystyle F_{2}\subset F_{1}^{\bot }}$). Ils sont alors automatiquement en somme directe : ${\displaystyle F_{1}\cap F_{2}=\{0\}}$. Ainsi deux plans de l'espace euclidien de dimension 3 ne peuvent être orthogonaux, en vertu de la formule de Grassmann.

Deux sous-espaces vectoriels ${\displaystyle F_{1}}$ et ${\displaystyle F_{2}}$ sont dits perpendiculaires quand ce sont leurs supplémentaires orthogonaux qui sont orthogonaux, c'est-à-dire quand ${\displaystyle F_{1}^{\bot }\subset F_{2}}$ (qui équivaut encore à ${\displaystyle F_{2}^{\bot }\subset F_{1}}$). Ainsi deux plans vectoriels de l'espace de dimension 3 sont perpendiculaires quand leurs droites normales sont orthogonales.

La notion de perpendicularité s'étend aux sous-espaces affines d'un espace euclidien : deux sous-espaces affines non vides ${\displaystyle {\mathcal {F}}_{1}}$ et ${\displaystyle {\mathcal {F}}_{2}}$ sont dits perpendiculaires quand leurs directions (qui sont des sous-espaces vectoriels) le sont[2]. On montre alors que ${\displaystyle {\mathcal {F}}_{1}\cap {\mathcal {F}}_{2}\neq \emptyset }$. En dimension 3, deux droites affines ne seraient, selon cette définition, jamais perpendiculaires. Aussi l'adapte-t-on comme suit pour justifier l'usage en géométrie classique : deux droites affines sécantes ${\displaystyle {\mathcal {D}}_{1}}$ et ${\displaystyle {\mathcal {D}}_{1}}$ seront dites perpendiculaires quand elles le sont dans le plan ${\displaystyle \langle {\mathcal {D}}_{1}\cup {\mathcal {D}}_{2}\rangle }$ d'elles engendrent.