Condition périodique aux limites

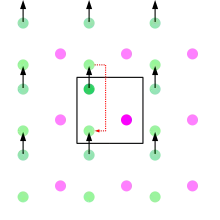
Les conditions périodiques aux limites sont particulièrement utiles en conjonction avec les méthodes de sommation d'Ewald (habituellement en maillage particulaire d'Ewald) pour prendre en compte les forces électrostatiques du système. Cependant, les conditions périodiques aux limites introduisent des artéfacts de corrélation qui ne respectent pas l'invariance de translation du système[2], et nécessite des contraintes de composition et de taille de la boîte de simulation. La charge électrostatique du système doit être nulle afin d'éviter une somme infinie lorsque la condition périodique aux limites lui est appliquée; cela est aisément assuré par l'addition d'ions (Na⁺, Cl⁻, etc.) en quantités appropriés si les molécules étudiées sont chargées. Comme dans les solutions réelles, de tels ions sont appelés contre-ions. Des ions sont parfois ajoutés à un système dans lequel les molécules étudiées sont neutres, afin d'approximer la force ionique d'une solution dans laquelle les molécules apparaissent naturellement. Le maintien de la convention d'image minimale requiert généralement qu'un rayon de coupure sphérique pour les forces non liantes soit d'au moins la moitié de la longueur d'un côté d'une boîte cubique. Même dans les systèmes électrostatiquement neutres, un moment dipolaire net de la maille unitaire peut introduire une fausse surface d'énergie volumique, équivalente à la pyroélectricité dans les cristaux polaires.
La taille de la boîte de simulation doit aussi être assez importante afin d'éviter que les artéfacts de périodicité créent des topologies non-physiques dans la simulation. Dans une boîte trop petite, un objet comme une macromolécule peut interagir de manière immédiate avec sa propre image dans une boîte voisine, ce qui est fonctionnellement équivalent à l'interaction, pour une molécule de sa « tête » avec sa « queue »[3]. Cela entraîne des dynamiques non-physiques de la plupart des objets comme les macromolécules, bien que l'intensité des conséquences et, par la suite, la taille appropriée pour la boîte par rapport à la taille des objets dépend de la durée - en temps virtuel - prévue de simulation, la précision voulue, et les comportements anticipés. Par exemple, les simulations du repliement de protéine qui commencent à partir d'un état natif peuvent produire des fluctuations plus faibles et donc peuvent ne pas nécessiter de boîtes de simulation aussi grandes que de partir d'une pelote aléatoire. Cependant, les effets des couches de solvatation sur les dynamiques observées - en simulation ou expérimentalement - ne sont pas bien compris, de manière générale. Une recommandation classique, issue des simulations sur l'ADN, est de prendre au moins 1 nm (10 Å) autour des molécules étudiées dans chaque dimension[4].

L'application de conditions périodiques aux limites impose à la boîte de simulation de posséder une forme compatible avec ces conditions, c'est-à-dire qui permet un pavage parfait d'un espace tridimensionnel. Par conséquent, une forme sphérique ou ellipsoïdale est à écarter. Une forme cubique ou de prisme rectangulaire est le choix le plus intuitif et le plus commun, mais peut s'avérer coûteux numériquement en raison de la présence d'objets dans les coins de boîte (comme des molécules de solvant), objets distants de l'objet d'étude (une macromolécule, par exemple). Une alternative commune qui nécessite un volume inférieur est l'utilisation d'un octaèdre tronqué.
L'étude d'un cristal parfait - d'un composé existant ou théorique[5] - présente l'avantage de pouvoir utiliser les conditions périodiques aux limites comme propriétés intrinsèques du système étudié, les symétries (groupes d'espaces) permettant de définir la boîte de simulation de manière non équivoque. L'introduction de défauts nécessite par conséquent l'augmentation de la taille de simulation.

Lorsqu'on simule un système physique en faisant appel aux conditions périodiques aux limites. Il faut, lors du post traitement, les prendre en compte pour calculer correctement la grandeur physique qu'on souhaite calculer (déplacement quadratique moyen, fonction de distribution radiale, paramètre d'ordre, etc.). Il faut donc appliquer la convention d'image minimale qui stipule :

${\displaystyle \Delta x=x_{i}-x_{j}={\begin{cases}\Delta x-L_{x}&{\mbox{ si }}\Delta x\geq {\frac {L_{x}}{2}}\\\Delta x+L_{x}&{\mbox{ si }}\Delta x\leq -{\frac {L_{x}}{2}}\\\Delta x&{\mbox{sinon}}\end{cases}}}$

Ici ${\displaystyle L_{x}}$ désigne la longueur de la boîte selon la direction ${\displaystyle x}$. Voici un exemple d'algorithme en Python :

#Définition de la fonction pour calculer les écarts entre atomes
#Ici lx est la longueur selon x et x_coord est l'ensemble des coordonnées selon cette même direction
def conditions_limites_1d(lx,x_coord):
    #Calcul des écarts entre chaque atome en évitant de calculer l'écart i-i et j-i
    deltax=[x_coord[i]-x_coord[j] for i in range(len(x_coord)) for j in range(len(x_coord)) if i!=j and j>i]
    #Application des conditions périodiques aux limites
    deltax[deltax > lx/2]-=lx
    deltax[deltax < -lx/2]+=lx
    return deltax

L'extension à trois dimensions s'inscrit dans la continuité de cet algorithme. La présente section considérant uniquement le cas d'une boîte cubique. Il fonctionne néanmoins si l'on considère une boîte parallélépipédique, il faut juste modifier les conditions sur les longueurs de boîte (car ${\displaystyle L_{x}\neq L_{y}\neq L_{z}}$ dans ce cas précis).

Dans le cadre des conditions périodiques aux limites, le moment linéaire du système sera conservé, mais le moment angulaire ne pourra l'être en raison de l'absence de symétrie de rotation - a priori - dans un système soumis à ces conditions. Lorsque l'on effectue une simulation dans l'ensemble microcanonique (nombre de particules, volume et énergie constante, noté sous forme abrégée en NVE) en appliquant les CPL, plutôt que des murs de réflexions qui modifient légèrement l'échantillonnage de simulation en raison de la conservation du moment linéaire total et de la position du centre de masse; cet ensemble est parfois appelé « ensemble de dynamique moléculaire »[6] ou ensemble NVEPG[7], bien que le terme de dynamique moléculaire puisse être - et est - appliqué à des simulations effectuées dans d'autres ensembles thermodynamiques. Ces conservations de quantités additionnelles introduisent des artéfacts mineurs liés à la définition de la température dans la mécanique statistique, à partir d'une distribution de vitesses basée sur une distribution de Boltzmann, et sur les violations de l'équipartition pour des systèmes contenant des particules à masses hétérogènes. Le plus simple de ces effets est qu'un système de N particules se comportera, dans l'ensemble NVE, comme un système de N-1 particules. Ces artéfacts ont des conséquences quantifiables pour des petits systèmes d'essai contenant uniquement des particules parfaitement dures; elles n'ont pas été jusqu'à présent étudiées en profondeur pour des systèmes plus complexes, comme des simulations de biomolécules standard, mais étant donné la taille de tels systèmes, on peut raisonnablement penser que ces effets seront fortement négligeables[7].

• Schlick T. (2002). Molecular Modeling and Simulation: An Interdisciplinary Guide. Interdisciplinary Applied Mathematics series, vol. 21. Springer: New York, NY, USA. (ISBN 0-387-95404-X). Voir esp. p. 272-6.
• Rapaport DC. (2004). The Art of Molecular Dynamics Simulation. 2nd ed. Cambridge University Press. (ISBN 0521825687). Voir esp. p. 15-20.