Cône (topologie)

• Le cône construit sur un point p de la droite réelle est le segment {p} × [0,1].
• Le cône construit sur deux points {0,1} est un "V" avec les extrémités en 0 et 1.
• Le cône construit sur un intervalle I de la droite réelle est un triangle plein, aussi appelé 2-simplexe (voir l'exemple final).
• Le cône construit sur un polygone P est une pyramide de base P.
• Le cône construit sur un disque est le cône solide de la géométrie classique (d'où le nom de ce concept).
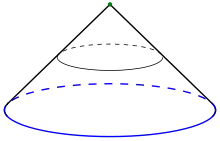
• Le cône construit sur un cercle est la surface du cône précédent :${\displaystyle \{(x,y,z)\in \mathbb {R} ^{3}\mid x^{2}+y^{2}=z^{2}{\mbox{ et }}0\leq z\leq 1\}.}$Ce dernier est homéomorphe au disque fermé.
• Plus généralement le cône construit sur une n-sphère est homéomorphe à la (n+1)-boule fermée.
• Le cône construit sur un n-simplexe est un (n+1)-simplexe.

Le cône d'un espace non vide est contractile (en particulier connexe par arcs et simplement connexe), puisqu'il se rétracte par déformation sur son sommet par l'homotopie h_t(x,s) = (x, (1–t)s).

Le cône est utilisé en topologie algébrique précisément parce qu'il transforme un espace en un sous-espace d'un espace contractile : X = X × {1} ⊂ CX.

Lorsque X est compact, le cône CX peut être visualisé comme la réunion des segments joignant tout point de X à un point unique. Cependant, cette image ne fonctionne plus si X n'est pas quasi-compact ou pas séparé, car généralement la topologie quotient sur CX est plus fine que la topologie de la réunion des segments joignant X à un point.

Si X est un CW-complexe, alors CX aussi[2]. Si deux espaces ont même type d'homotopie, leurs cônes aussi.

Si f : X → Y est une fonction continue, on définit le cône C_f de l'application f comme le quotient de la réunion disjointe CX⊔Y par l'identification de chaque élément x de X ⊂ CX avec son image f(x) dans Y. L'inclusion de Y dans C_f est alors une cofibration.

Le cône de l'application identité de X est CX. Celui de l'écrasement de CX sur un point est la suspension SX de X.

Si (X, x₀) est un espace pointé, son cône réduit est

${\displaystyle \mathrm {C} _{*}(X,x_{0})=X\times [0,1]/\left[(X\times \left\{0\right\})\cup (\left\{x_{0}\right\}\times [0,1])\right],}$

muni de la topologie quotient[4] et pointé par l'image, dans ce quotient, du couple (x₀, 0). L'inclusion naturelle de l'espace pointé dans son cône respecte ce pointage.

De même que le cône d'un espace non pointé est le cône de son application identité, le cône réduit d'un espace pointé est le cône réduit de son application identité.

L'application X ↦ CX induit un foncteur C : Top → Top sur la catégorie des espaces topologiques. L'application continue Cf[5] de CX vers CY associée à une application continue f : X → Y est définie par : Cf([(x, t)]) = [(f(x), t)][6]. On a de même un foncteur C_✻ sur la catégorie des espaces pointés.

• Joint (mathématiques)
• Cylindre (topologie)