Recollement (topologie)
En mathématiques, le recollement est la construction d'un espace topologique obtenu en « attachant un espace à un autre le long d'une application ». Plus précisément[1] - [2], on attache un espace Y à un espace X, le long d'une application f à valeurs dans X, continue sur un sous-espace A de Y, en définissant l'espace X ∪f Y comme le quotient de la somme topologique (en) X⊔Y par la relation d'équivalence qui identifie chaque élément de A à son image par f. C'est un cas particulier de somme amalgamée.
Propriétés
L'ensemble quotient (sans sa topologie) est canoniquement en bijection avec la réunion disjointe X⊔(Y\A).
Si A est fermé dans Y, le plongement X → X ∪f Y est une application fermée et le plongement(Y\A) → X ∪f Y est une application ouverte.
Si A est ouvert (resp. fermé) et f est ouverte (resp. fermée), l'application X⊔Y → X ∪f Y de passage au quotient est ouverte (resp. fermée)[3].
Exemples
- Le recollement de « cellules » est l'opération de base dans la définition inductive des CW-complexes. L'espace Y est dans ce cas une n-boule fermée et le sous-espace A est son bord, la (n – 1)-sphère.
- Le recollement est aussi utilisé pour définir des sommes connexes de variétés. Ici, on retire d'abord à chacune des deux variétés une boule ouverte, avant d'attacher entre eux les bords sphériques de ces deux boules.
- Le wedge de deux espaces pointés est le recollement des deux espaces le long de l'application qui envoie le point base de l'un sur celui de l'autre.
- Le quotient Y/A correspond au cas particulier de recollement dans lequel X est réduit à un point.
- La « droite réelle avec un point double » est le recollement de deux copies de ℝ le long de l'ouvert ℝ*.
Description catégorique
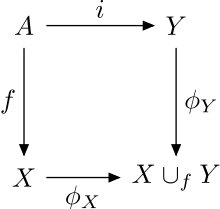
Le recollement est un exemple de somme amalgamée dans la catégorie des espaces topologiques. En effet, X ∪f Y est la solution du problème universel correspondant au diagramme commutatif suivant, où i est l'injection canonique :
Notes et références
- Claude Godbillon, Éléments de topologie algébrique [détail de l’édition], p. 27.
- (en) « Adjunction space », sur PlanetMath.
- (en) I. M. James, General Topology and Homotopy Theory, Springer, (lire en ligne), p. 46.
Voir aussi
Articles connexes
Bibliographie
- (en) Ronald Brown, Topology and Groupoids, BookSurge, , 3e éd., 512 p. (ISBN 978-1-4196-2722-4)
- (en) Stephen Willard, General Topology, Mineola, N.Y., Dover, (1re éd. 1970), 369 p. (ISBN 978-0-486-43479-7, lire en ligne)