Arrondi (mathématiques)
Arrondir un nombre consiste à le remplacer par un autre nombre considéré comme plus simple ou plus pertinent. Ce procédé s'appelle arrondissage ou arrondissement et le nombre obtenu est un arrondi.
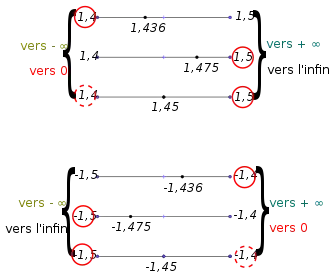
Entouré en rouge, l'arrondi au plus proche.
Entouré en rouge pointillé, le plus proche pair en cas d'équidistance.
Le résultat est moins précis, mais plus facile à employer. Il y a plusieurs façons d'arrondir. En général, on arrondit un nombre en en donnant une valeur approchée obtenue à partir de son développement décimal en réduisant le nombre de chiffres significatifs. L'arrondi peut se faire au plus proche, par excès ou par défaut.
Par exemple, l'arrondi entier de 7,3 est 7.
Motivations
En mathématiques, on peut être amené à manipuler des nombres ayant beaucoup de décimales, voire une infinité dont seulement certaines sont connues avec exactitude, il est alors plus pratique de limiter le résultat final à un nombre raisonnable de décimales. Par exemple π a un nombre infini de décimales, dont beaucoup sont inutiles pour évaluer un périmètre. En arrondissant π à 3,14, on commet une erreur absolue sur π inférieure à 2.10-3 et une erreur relative sur le produit inférieure à 7.10-4, ce qui est souvent suffisant.
Ce même problème apparait lors de constructions de tables numériques ou lors de la manipulation de nombres dans les calculateurs. La précision des nombres est limitée par la place qu'on leur réserve dans la table ou dans la mémoire. Des arrondis apparaissent nécessairement qu'il faut apprendre à maitriser et contrôler[1].
Dans les applications pratiques, les valeurs numériques peuvent avoir une précision illusoire comme la population des États-Unis recensée en 2020 (331 449 281 habitants[2]). Ce nombre gagne à être arrondi à la centaine de milliers près (331,5 millions) ou au million près (331 millions) ou à un autre ordre de grandeur. D'autres quantités ne sont connues qu'approximativement car elles dépendent de la précision des instruments employés. Elles ne sont connues qu'à une incertitude près. Effectuer des calculs et fournir un résultat final dont la précision serait meilleure que l'incertitude initiale n'a pas d'intérêt[3]. Si des mesures sont faites au mm près, par exemple, pour les côtés de l'angle droit d'un triangle rectangle, calculer l'hypoténuse et donner un résultat au micron est un non-sens : pour une incertitude de mesure au mm, un arrondi au dixième de millimètre est suffisant[4].
Dans le domaine monétaire, il arrive que des calculs liés à l'application de pourcentages (TVA, taux de réduction, ...) ou de conversions conduisent à un résultat dont l'unité est inférieure à la plus petite dénomination de la devise en cours. Il est alors nécessaire d'arrondir ce résultat à un multiple de la plus petite devise en circulation. Ainsi on ne présente pas de facture donnant les dixièmes de centime d'euro, on arrondit au centime d'euro, voire à l'euro. C'est l'arrondi monétaire.
On peut aussi décider d'opérer un arrondi solidaire, arrondissant par excès une facture en caisse[5], ou par défaut un salaire[6] de telle sorte que l'excédent ou le déficit soit reversé à une association.
Techniques d'arrondis
Arrondi au plus proche
L'arrondi au plus proche d'un nombre x à 10-n est le multiple de 10-n le plus proche de ce nombre[7].
Ainsi
- l'arrondi au centième de 1,471 est 1,47, celui de 1,476 est 1,48 celui de -1,471 est -1,47
- l'arrondi à l'unité de 8,37 est 8, celui de -17,62 est -18.
- l'arrondi au millier de 135 786 est 136 000
L'arrondi d'un nombre réduit le nombre de chiffres significatifs et introduit une erreur d'arrondi majorée en valeur absolue par[8] 0,5.10-n.
Il arrive que le nombre x soit à égale distance de deux multiples de 10-n. Cela se produit quand les chiffres négligés sont 5 suivi d'une infinité de 0. Dans ce cas, il y a ambiguïté sur le multiple de 10-n à prendre. Plusieurs choix sont possibles et donnent lieu aux variantes suivantes.
Arrondi arithmétique
C'est l'arrondi privilégié en mathématique élémentaire[9]. Cela consiste, pour un nombre positif, à regarder le chiffre qui suit le dernier chiffre retenu.
- si ce chiffre suivant est 0, 1, 2, 3, ou 4, on ne retient que les chiffres précédents sans les modifier (arrondi par défaut).
- si ce chiffre suivant est 5, 6, 7, 8, 9 , on retient les chiffres précédents en augmentant d'une unité le dernier chiffre (arrondi par excès).
Dans cette convention, l'ambiguïté est levée en prenant, pour un nombre positif, l'arrondi par excès.
| Chiffres retenus (soulignés) premier chiffre négligé (en gras) | Arrondi | Remarque | |
|---|---|---|---|
| à la dizaine | 183,9525 | 180 | ou plus exactement 1,8.101 soit 2 chiffres significatifs[8] |
| à l'unité | 183,9525 | 184 | |
| au dixième | 183,9525 | 184,0 | L'ajout d'une unité entraine une retenue. Il faut conserver le 0 qui est significatif. |
| au centième | 183,9525 | 183,95 | |
| au millième | 183,9525 | 183,953 | Il y a ambiguïté. La convention choisit l'arrondi par excès. |
Cette notion d'arrondi (prendre l'entier le plus proche, et s'il y a plusieurs candidats prendre le plus grand en valeur absolue) est la plus courante dans les logiciels grand public. Elle est notamment mise en œuvre dans :
- les calculatrices Texas Instruments et Casio,
- les logiciels Microsoft Excel[10], LibreOffice Calc[11], GeoGebra, GNU Octave,
- le langage C qui, par ailleurs, n'arrondit qu'à l'unité[12].
Cette notion d'arrondi présente cependant l'inconvénient d’introduire un biais statistique lors d'accumulation de calculs d'arrondis sur des nombres positifs, puisque l'on arrondit alors systématiquement par excès dans les cas ambigus. D'autres conventions sont parfois utilisées dans des logiciels spécialisés pour éviter ce biais statistique, la plus courante étant l'arrondi au pair le plus proche.
Arrondi au pair le plus proche
La seule différence entre l'arrondi au pair le plus proche et l'arrondi présenté plus haut réside dans le traitement des cas ambigus : lorsqu'un nombre est équidistant de deux multiples consécutifs, on prend pour l'arrondi le multiple pair.
Par exemple :
- l'arrondi au pair le plus proche à 10-2 près de 8,125 est 8,12,
- l'arrondi au pair le plus proche à 10-1 près de -1,35 est -1,4.
Cette variante est notamment mise en œuvre dans :
- les micro-processeurs pour les nombres à virgule flottante (norme IEEE 754)[13],
- les logiciels Mathematica[14] et Maxima (qui arrondit à l'unité)[15], le langage Python[16]
- Les langages R[17] et MySQL[18] arrondissent en principe les flottants, en cas d’ambiguïté, au pair le plus proche mais avec des comportements inattendus selon le caractère représentable du nombre.
- DotNet arrondit ses flottants, en cas d’ambiguïté, par défaut, au pair le plus proche mais offre des options pour changer la règle[19].
Cas des nombres négatifs
Idéalement, on souhaite que l'arrondi au plus proche soit une fonction paire[20]. Cela est réalisé si l'arrondi est effectué sur la valeur absolue du nombre[21].
- l'arrondi au plus proche à 10-1 près de -1,47 est -1,5
- l'arrondi au plus proche à 10-1 près de -1,43 est -1,4
- l'arrondi au plus proche à 10-1 près de -1,45 est -1,5 (arrondi arithmétique) ou -1,4 (arrondi au pair)
Pour l'arrondi arithmétique à 10-n, cela revient à appliquer la formule où est la fonction donnant le signe du nombre, E est la fonction partie entière, et |...| la fonction valeur absolue.
Mais cette convention n'est pas universelle : certains sites[22] règlent l'ambiguité en proposant d'arrondir systématiquement par excès même pour les nombres négatifs, proposant -3,4 comme arrondi au plus proche de -3,45. Le langage Java utilise, pour son arrondi à l'unité, la formule[23]: qui n'est pas une fonction paire.
Quand un nombre est arrondi à zéro, il est parfois représenté par un zéro signé, en particulier, lorsqu'un nombre négatif est arrondi à zéro, le résultat de l'arrondi est parfois noté -0 pour indiquer ce fait. C'est notamment le cas en météorologie pour les températures.
Généralisation à une base quelconque
Cette définition de l'arrondi au plus proche à 10-n pour un nombre en écriture décimale s'étend naturellement à l'arrondi au plus proche à b-n pour un nombre écrit en base b, en particulier en base 2 utilisée dans les ordinateurs.
Donald Knuth, par exemple, dans son travail sur l'écriture en virgule flottante, définit en base b l'arrondi au plus proche à p places pour un nombre f dont la valeur absolue est dans l'intervalle [1/b ; 1[ sous la forme suivante[7]:
- l'arrondi de f à p places est le multiple de b-p le plus proche de f.
Pour lever le cas de l'équidistance, pour b pair, il choisit pour l'arrondi f ', le multiple de b-p tel que bp.f '+ b/2 est impair.
Cette définition est compatible avec l'arrondi au pair en base 10.
Autres arrondis
D'autres méthodes arrondissent de différentes manières. Tous les arrondis qui suivent (à l'exception de l'arrondi au multiple) provoquent une erreur d'arrondi inférieure ou égale à 10-n.
Arrondi vers + ∞
L'arrondi vers + ∞ , ou arrondi par excès, à 10-n près de x est le multiple de 10-n, supérieur ou égal à x, le plus proche de x.
Il est proposé dans de nombreux langages sous la forme Ceiling (Wolfram[24]), souvent seulement à l'unité ( Maxima[25], R[17], Mysql[26], DotNet[27]).
Arrondi vers - ∞
L'arrondi vers - ∞ , ou arrondi par défaut, à 10-n près de x est le multiple de 10-n, inférieur ou égal à x, le plus proche de x.
Il est proposé dans de nombreux langages sous la forme Floor (Wolfram[28]), souvent seulement à l'unité (Maxima[25] , R[17], Mysql[29], DotNet[30]).
Arrondi vers zéro
L'arrondi vers zéro, ou troncature, à 10-n près de x est le multiple de 10-n le plus proche de x qui lui soit plus petit en valeur absolue.
Cet arrondi se comporte comme l'arrondi vers - ∞ pour les valeurs positives et comme l'arrondi vers + ∞ pour les valeurs négatives[20].
Il est proposé dans de nombreux langages sous le forme Arrondi.Inf (Excel [31], OpenOffice[32]) ou Truncate (Maxima[25] à l'unité, Mysql[33], DotNet[34] à l'unité) ou Trunc (R[17] à l'unité)
Arrondi vers l'infini
Certains logiciels (Excel [35], OpenOffice[36]) proposent un arrondi vers l'infini comme le multiple de 10-n le plus proche de x qui lui soit plus grand en valeur absolue.
Arrondi au multiple
Toutes les méthodes précédentes peuvent s'appliquer à des arrondis, non à un multiple d'une puissance de 10, mais à un multiple d'un nombre quelconque. Cela peut se révéler utile quand on cherche une précision intermédiaire. Par exemple, si on cherche à arrondir des sommes en euros au 5 cents le plus proche, on arrondira les valeurs 3,41 € et 3,42 € à 3,40 €, celles entre 3,43 € et 3,47 € à 3,45 € et les valeurs 3,48 € et 3,49 € à 3,50 €.
Certains langages informatiques ont mis en place ce type d'arrondi comme Excel et Libreoffice avec leurs fonctions ARRONDI.AU.MULTIPLE[37] - [38], PLANCHER[39] - [40], PLAFOND[41] - [42].
Tableau comparatif
| Nombre | Arrondi arithmétique | Arrondi au pair | Arrondi vers 0 | Arrondi vers - ∞ | Arrondi vers + ∞ |
|---|---|---|---|---|---|
| 1,42 | 1,4 | 1,4 | 1,4 | 1,4 | 1,5 |
| -1,42 | -1,4 | -1,4 | -1,4 | -1,5 | -1,4 |
| 1,46 | 1,5 | 1,5 | 1,4 | 1,4 | 1,5 |
| -1,45 | -1,5 | -1,4 | -1,4 | -1,5 | -1,4 |
Normes et conventions
En informatique, la norme IEEE 754 est employée pour le calcul avec des nombres à virgule flottante ; elle provient d'une étude théorique approfondie sur les propriétés que doivent avoir l'arrondi pour garantir le minimum d'erreurs et la stabilité des résultats lors de suites de calculs[43].
Dans le domaine monétaire, l'usage le plus courant semble être l'arrondi au plus proche avec arrondi par excès en cas d’ambiguïté. C'est notamment le cas pour le montant imposable et le montant de l'impôt arrondi en France à l'euro le plus proche[44]. C'est également le cas pour les conversions de devises vers l'euro (et vice-versa) dans la zone euro dont les taux sont fixés par la Banque centrale européenne et les résultats arrondis au cent le plus proche[45]. Et c'est encore le cas pour les pays tels la Finlande, les Pays-Bas, la Belgique, l’Irlande et l’Italie[46] qui ont décidé d'arrondir les achats en liquide au 5 cents le plus proche, de manière à limiter la circulation des pièces de 1 et 2 cents[47].
En métrologie, le choix de l'ordre de grandeur de l'arrondi est déterminé en fonction de celui de l'incertitude. La norme AFNOR NF X 06 -044 précisait que l'erreur due à l'arrondissage devait être inférieure au dixième de l'incertitude. En pratique, on regarde l'ordre de grandeur et le premier chiffre significatif de l'incertitude. Si le premier chiffre significatif de l'incertitude est compris entre 5 et 9, on arrondit le nombre à l'ordre de grandeur de l'incertitude, si le chiffre significatif est inférieur à 5, on arrondit à l'ordre inférieur[4].
Historique
Le concept d'arrondi est très ancien puisqu'on a des preuves d'arrondissage de nombres dans les mathématiques mésopotamiennes dès la période d'Isin-Larsa. La troncature, motivée par la taille des abaques était utilisée pour simplifier des calculs ou travailler sur des nombres non réguliers (comme l'inverse de 7) . Les scribes étaient formés à l'usage des arrondis et conscients des erreurs qu'ils induisaient qu'ils cherchaient à compenser[48].
Les problèmes d'arrondis deviennent cruciaux dans la constitution de tables où les arrondis des calculs intermédiaires peuvent propager des erreurs rendant non sûre la dernière décimale. Les fabricants de tables sont donc obligés d'effectuer les calculs avec des décimales de garde. Le problème est assez maitrisable lorsque l'on dispose de valeurs pivots dont on connait un arrondi correct et que l'on procède à un nombre raisonnable d'interpolation. C'est le cas de la table des sinus de Régiomontanus qui a probablement utilisé deux (et parfois une) décimales de garde pour sa table de sinus[49]. Mais pour arriver à une bonne précision dans une table de logarithmes, le nombre de décimales de garde devient vite plus important[50]. John Napier, par exemple, travaille sur 14 chiffres significatifs pour un arrondi à 7 chiffres[51]. Cette préoccupation perdure dans les calculs actuels sont le nom de « Dilemme du fabricant de tables ».
La généralisation des calculs par ordinateurs entraine des erreurs d'arrondis dont certaines sont devenues célèbres par leurs conséquences : explosion d'un missile lors de la Guerre du Golfe (1991), échec d'Ariane 5 (1996), attributions indues de sièges dans des élections (Schleswig-Holstein - 1992)[52] - [53].
Certaines des erreurs précédentes sont dues à une mauvaise communication sur la nature de l'arrondi opéré. La diversité des arrondis possibles avec des résultats très différents ont poussé à la création de normes (en informatique) ou de directives (dans le domaine monétaire)[54].
En 1985, la norme IEEE 754 impose l'arrondi correct pour les quatre opérations de base et la racine carrée. La recherche se poursuit pour fournir des arrondis corrects sur les principales fonctions mathématiques. En 2001 et 2002, des bibliothèques de fonctions avec arrondis correct apparaissent (IBM et Sun)[55]. En 2019, la norme IEEE 754 révisée recommande l'arrondi correct pour les fonctions de base (logarithmes, exponentielles, trigonométriques...)[56].
Articles connexes
Notes et références
- Lauter 2008, p. 1;2.
- (en) « 2020 Census Apportionment Results Delivered to the President », sur Census.gov
- Petite Encyclopédie, p. 660.
- Arrondissage CEA.
- Marie Mougin, « L'arrondi en caisse : un don solidaire qui peut lever 80 000 euros en une seule semaine ! », sur France Inter,
- « L’arrondi sur salaire, une autre façon d’être solidaire », sur Handicap-International
- Knuth 1997, p. 217.
- Petite Encyclopédie, p. 662.
- Hélène Audren, Serge Cecconi et Eric Le Goff, Maths, 4e : programme 2007, Bréal, p. 12
- Patrice Rey, Mathématique, Statistique et Finance (2eme edition): avec Excel 2016 (lire en ligne), p. 71
- « ARRONDI - The Document foundation wiki »
- « Round, roundf, roundl | Microsoft Docs ».
- Thibaut Balabonski, Sylvain Conchon, Jean-Christophe Filliâtre et Kim Nguyen, Spécialité Numérique et sciences informatiques : 30 leçons avec exercices corrigés - Première - Nouveaux programmes, Ellipses, , p. 255
- (en) « Round - Wolfram Language documentation » - Properties & Relations
- (en) « Functions for Numbers (Maxima 5.45.0 Manual) » - function Round
- « Fonctions natives — Documentation Python 3.7.13 » - round
- (en) « Round function - RDocumentation »
- (en) « MySQL :: MySQL 5.7 Reference Manual :: 12.22.4 Rounding Behavior »
- « Math.Round Méthode (System) | Microsoft Docs »
- Defour 2003, p. 15.
- « Mathematics 2 », sur scientificsentence.net
- « Arrondissement | Lexique mathématique », sur lexique.netmath.ca
- (en) « Java Math round() method with Example », sur www.geeksforgeeks.org
- « Ceiling ([...])—Wolfram Language Documentation »
- « Functions for Numbers (Maxima 5.45.0 Manual) »
- « MySQL :: MySQL 5.7 Reference Manual :: 12.6.2 Mathematical Functions »
- « Math.Ceiling Méthode (System) | Microsoft Docs »
- « Floor ( »
- « MySQL :: MySQL 5.7 Reference Manual :: 12.6.2 Mathematical Functions »
- « Math.Floor Méthode (System) | Microsoft Docs »
- « ARRONDI.INF() : arrondir au nombre inférieur - DocExcel », sur docexcel.com
- « FR/Documentation/Calc: fonction ARRONDI.INF — Apache OpenOffice Wiki », sur wiki.openoffice.org
- « MySQL :: MySQL 5.7 Reference Manual :: 12.6.2 Mathematical Functions »
- « Math.Truncate Méthode (System) | Microsoft Docs »
- « ARRONDI.SUP() : arrondir au nombre supérieur - DocExcel », sur docexcel.com
- « FR/Documentation/Calc: fonction ARRONDI.SUP — Apache OpenOffice Wiki », sur wiki.openoffice.org
- « ARRONDI.AU.MULTIPLE() : arrondir au multiple - DocExcel », sur docexcel.com
- « ARRONDI.AU.MULTIPLE », sur wiki.documentfoundation.org
- « PLANCHER() : arrondir au multiple inférieur - DocExcel », sur docexcel.com
- « PLANCHER », sur wiki.documentfoundation.org
- « PLAFOND() : arrondir au multiple supérieur - DocExcel », sur docexcel.com
- « PLAFOND », sur wiki.documentfoundation.org
- Article de Vincent Lefèvre et Jean-Michel Muller sur cette étude.
- « Article 26 - Loi n° 98-546 du 2 juillet 1998 portant diverses dispositions d'ordre économique et financier (1). - Légifrance », sur legifrance.gouv.fr
- « Introduction - Circulaire-LGA_60_LIR_-23-3_ICC_39_EVAL_59_I_FORT_49_du-21_6_2016.pdf », sur impotsdirects.public.lu - Généralités - p.3
- « 20 ans de l'euro : les réponses à vos questions sur la monnaie unique - Touteleurope.eu », sur www.touteleurope.eu - Des nouveaux billets en 2024 ?
- « Arrondi des paiements en espèce », sur economie.fgov.be.
- Robert Middeke-Conlin, The Making of a Scribe : Errors, Mistakes and Rounding Numbers in the Old Babylonian Kindom of Larsa, Springer, (présentation en ligne) pp.229;231;233
- (en) Denis Roegel, « A survey of the main fundamental European trigonometric tables printed in the 15th and 16th centuries. », Rapport de recherche, (HAL hal-03330572)
- Lauter 2008, p. 1.
- (en) Denis Roegel, « Napier’s ideal construction of the logarithms », 2012 (révisé 2021), p. 6
- (en) Lav Varshey, « The Deadly Consequences of Rounding Errors », sur slate.com,
- (en) « Disasters due to rounding error », sur Département de mathématiques de l'université du Texas - Austin
- Voir par exemple la normalisation opérée en France en 1998 - « Projet de loi sur l'habilitation du Gouvernement à adapter par ordonnance la valeur en euros de certains montants exprimés en francs dans les textes législatifs », sur Senat.fr Rapport 372 (1999-2000) - Commission des finances - I.B. Les dispositions nationales)
- Lauter 2008, p. 2.
- IEEE Computer Society, « IEEE Standard for Floating-Point Arithmetic », IEEE STD 754-2019, , p. 1–84 (ISBN 978-0-7381-5753-5, DOI 10.1109/IEEESTD.2008.4610935)
Bibliographie
- M. Bé, P. Blanchis, C. Dulieu, « Arrondissage des résultats de mesure, nombre de chiffres significatifs », BNM, CEA, laboratoire national Henri Becquerel,
- David Defour, « Fonctions élémentaires : algorithmes et implémentations efficaces pour l'arrondi correct en double précision », École normale supérieure de Lyon,
- (en) Donald Knuth, The Art of Computer Programming, vol. 2, Addison-Wesley, , « Chap.IV »
- W Gellert, H. Küstner, M. Hellwich et H. Kästner, Petite encyclopédie des mathématiques, Didier,
- Jean-Michel Muller, Arithmétique des ordinateurs, Masson, , 214 p. (ISBN 2-225-81689-1, lire en ligne)⟨ensl-00086707⟩
- Vincent Lefèvre et Jean-Michel Muller, « Erreurs en arithmétique des ordinateurs », Images des mathématiques, (lire en ligne)
- Christoph Quirin Lauteur, « Arrondi correct de fonctions mathématiques (Thèse) », sur ENS-Lyon,


