Structure d'incidence
En mathématiques, une structure d'incidence est toute composition de deux types d'objets dans le plan euclidien : des points ou l'équivalent de points et des droites ou l'équivalent de droites et d'une seule relation possible entre ces types, les autres propriétés étant ignorées et la structure pouvant ainsi se représenter par une matrice. Cette réduction de la complexité est à l'origine de l'émergence du concept dans d'autres domaines sous des formes propres.

Exemple 1: Points et droites du plan euclidien
Exemple 2: Points et cercles
Exemple 3: Structure définie par une matrice d'incidence.
Les structures d'incidence sont le plus souvent considérées dans le contexte géométrique d'où elles sont abstraites, et donc généralisées, tels que les plans affines, projectifs ou de plan de Möbius, mais le concept est plus large et ne se limite pas aux propriétés géométriques. Même dans un environnement géométrique, les structures d'incidence ne se limitent pas aux seuls points et droites ; des objets de plus grande dimension (plans, solides, espaces de dimension n, coniques, etc.) peuvent être vus sous cet angle. L'étude des structures finies est parfois appelée la géométrie finie[1].
Définition formelle et terminologie
Une structure d'incidence est un triplet ( P, D, I ), où P est un ensemble dont les éléments sont appelés points, D est un ensemble distinct dont les éléments sont appelés droites et I ⊆ P × D est la relation d'incidence . Les éléments de I s'appellent des drapeaux. Si ( p, d ) est dans I alors on dit que le point p « se trouve sur » la droite d ou que la droite d « passe par » le point p . Une terminologie plus symétrique, qui reflète la nature symétrique de cette relation, est que « p est incident à d » ou que « d est incident à p » et utilise la notation p I d synonyme de (p, d) ∈ I[2].
Fréquemment D est une famille de sous-ensembles de P auquel cas l'incidence I est l'appartenance ( p I d si et seulement si p est élément de d ). Les structures d'incidence de ce type sont appelées ensemblistes[3]. Ce n'est pas toujours le cas ; par exemple, si P est un ensemble de vecteurs et D un ensemble de Matrices carrées, on peut définir I = {(v, M) : vecteur v est un vecteur propre de la matrice M }. Cet exemple montre également que si le langage géométrique des points et des lignes est utilisé, les types d'objet n'ont pas besoin d'être ces objets géométriques.
Exemples
Une structure d'incidence est uniforme si chaque droite est incidente au même nombre de points. Chacun de ces exemples, à l'exception du second, est uniforme avec trois points par droite.
Graphes
Tout graphe (pas nécessairement simple ; éventuellement avec boucles et arêtes multiples ) est une structure d'incidence uniforme avec deux points par droite. Dans ces exemples, les sommets du graphe forment l'ensemble de points, les arêtes du graphe forment l'ensemble de droites et l'incidence signifie qu'un sommet est une extrémité d'une arête.
Espaces linéaires
Les structures d'incidence sont rarement étudiées dans leur pleine généralité; il est plus usuel d'étudier les structures d'incidence qui satisfont certains axiomes supplémentaires. Par exemple, un espace linéaire partiel est une structure d'incidence qui satisfait les deux conditions suivantes :
- Deux points distincts sont incidents à au plus une même droite commune, et
- chaque droite est incidente à au moins deux points.
Si le premier axiome est remplacé par l'axiome plus fort :
- Deux points distincts sont incidents à exactement une même droite commune,
la structure d'incidence est appelée un espace linéaire[4].
Réseaux
Un exemple plus spécialisé est un k-réseau ; c'est une structure d'incidence dans laquelle les droites sont réparties en k classes parallèles, de sorte que deux droites de la même classe parallèle n'ont pas de point en commun, mais deux droites de classes différentes ont exactement un point en commun, et chaque point appartient à exactement une droite de chaque classe parallèle. Un exemple de k-réseau est l'ensemble des points d'un plan affine avec k classes parallèles de droites affines.
Structure duale
Si on échange le rôle des "points" et des "droites" dans
- C = (P, D, I)
on obtient la structure duale :
- C∗ = (D, P, I∗),
où I∗ est la relation inverse de I. Il découle immédiatement de la définition que :
- C∗∗ = C.
Il s'agit d'une version abstraite de la dualité projective[2].
Une structure C isomorphe à sa duale C∗ est appelée auto-duale. Le plan de Fano ci-dessus est une structure d'incidence auto-duale.
Une autre terminologie
Le concept de structure d'incidence est très simple et est apparu dans plusieurs disciplines, chacune introduisant son propre vocabulaire et spécifiant le genre de questions qui sont généralement posées sur ces structures. Les structures d'incidence utilisent une terminologie géométrique, mais en termes de théorie des graphes, elles sont appelées Hypergraphes et en termes de théorie du design, elles sont appelées plans en blocs . Elles sont également connues sous le nom de système d'ensembles ou de famille d'ensembles dans un contexte général.
Hypergraphes
Tout hypergraphe ou famille d'ensemble peut être considéré comme une structure d'incidence dans laquelle l'ensemble universel joue le rôle des "points", la famille d'ensembles correspondante joue le rôle de "droites" et la relation d'incidence est l'appartenance ensembliste "∈". Inversement, chaque structure d'incidence peut être considérée comme un hypergraphe en identifiant les droites avec les ensembles de points qui y sont incidents.
Bloc design
Un plan en blocs est, en toute généralité, composé d'un ensemble X et d'une famille de sous-ensembles de X (un sous-ensemble peut y figurer plusieurs fois). Normalement, un plan en blocs doit satisfaire des conditions de régularité numérique. En tant que structure d'incidence, X est l'ensemble des points et F est l'ensemble des droites, généralement appelées blocs dans ce contexte (les blocs répétés doivent avoir des noms distincts, donc F est en fait un ensemble et non un multiensemble). Si tous les sous-ensembles de F ont la même taille, le plan en blocs est appelé uniforme. Si chaque élément de X apparaît dans le même nombre de sous-ensembles, le plan de bloc est dite régulier. Le dual d'un plan de bloc uniforme est un plan régulier et vice-versa.
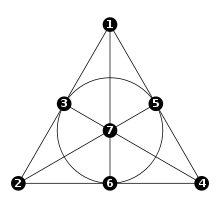
Exemple: plan de Fano
On considère le plan de bloc (ou hypergraphe) donné par:
- ,
- .
Cette structure d'incidence est appelée le plan de Fano. En tant que plan en bloc, il est à la fois uniforme et régulier.
Dans l'étiquetage donné, les droites sont précisément les sous-ensembles constitués de trois points dont les étiquettes s'additionnent à zéro en utilisant l'addition nim. De façon équivalente, chaque nombre, lorsqu'il est écrit en binaire, peut être identifié avec un vecteur non nul de longueur trois sur le corps binaire GF(2). Trois vecteurs qui génèrent un sous-espace vectoriel forment une droite; dans ce cas, cela équivaut à ce que leur somme vectorielle soit le vecteur nul.
Représentations
Les structures d'incidence peuvent être représentées de plusieurs manières. Si les ensembles P et D sont finis, ces représentations peuvent coder de manière compacte toutes les informations pertinentes concernant la structure.
Matrice d'incidence
La matrice d'incidence d'une structure d'incidence (finie) est une matrice binaire dont les lignes sont indexées par les points {pi } et les colonnes indexées par les droites {dj }, et où l'entrée i,j est un 1 si pi I dj et 0 sinon[5]. Une matrice d'incidence n'est déterminée de manière unique seulement par l'ordre choisi sur les points et les lignes[6].
La structure d'incidence non uniforme donnée ci-dessus (exemple numéro 2) est définie par:
- P = {A, B, C, D, E, P}
- D = { l = {C, P, E}, m = {P}, n = {P, D}, o = {P, A}, p = {A, B}, q = {P, B} }.
Une matrice d'incidence pour cette structure est:
qui correspond à la table d'incidence :
I l m n o p q A 0 0 0 1 1 0 B 0 0 0 0 1 1 C 1 0 0 0 0 0 D 0 0 1 0 0 0 E 1 0 0 0 0 0 P 1 1 1 1 0 1
Si une structure d'incidence C a une matrice d'incidence M, alors la structure duale C∗ a comme matrice d'incidence la matrice transposée M T (et elle est définie par cette matrice).
Une structure d'incidence est auto-duale s'il existe un ordre sur les points et les droites pour lesquels la matrice d'incidence est symétrique.
Avec les étiquettes données dans l'exemple numéro 1 ci-dessus et avec les points ordonnés A, B, C, D, G, F, E et les lignes ordonnées l, p, n, s, r, m, q, le plan de Fano a la matrice d'incidence :
Comme la matrice est symétrique, le plan de Fano est une structure d'incidence auto-duale.
Représentations figuratives
Une représentation figurative d'une structure d'incidence est construite en représentant les points de la structure par des points dans un plan et les droites par un des moyens visuels adapté pour joindre les points[6]. Les points peuvent être placés de manière arbitraire, sans restriction sur les distances entre les points ou les relations entre les points. Dans une structure d'incidence, les concepts de point situé entre deux autres points ou d'ordre d'alignement de points sur une droite ne sont pas définies. Par opposition, la géométrie ordonnée a une notion d'entre-deux (betweenness). Les mêmes observations peuvent être faites à propos des représentations des droites. En particulier, les droites ne sont pas nécessairement représentées par des segments de droite (exemples 1, 3 et 4). Comme dans la représentation figurative des graphe (mathématiques discrètes)s, le croisement de deux droites en un lieu autre qu'un point n'a pas de signification en termes de structure d'incidence; ce n'est qu'un effet de la représentation. Ces figures d'incidence peuvent parfois ressembler à des graphes, mais ce ne sont pas des graphes, à moins que la structure d'incidence ne soit un graphe.
Réalisabilité
Les structures d'incidence peuvent être modélisées par des points et des courbes dans le plan euclidien avec la signification géométrique habituelle de l'incidence. Certaines structures d'incidence admettent une représentation par des points et des droites rectilignes. Ces structures peuvent être appelées réalisables. Le plan de Fano (exemple 1 ci-dessus) n'est pas réalisable car il nécessite au moins une ligne courbe. La configuration Möbius-Kantor (exemple 4 ci-dessus) n'est pas réalisable dans le plan euclidien, mais elle l'est dans le plan complexe[7] Les exemples 2 et 5 ci-dessus sont réalisables et les figures d'incidence données le démontrent. Ernst Steinitz, dans sa thèse de 1894[8] a montré qu'une n3-configuration (une structure d'incidence avec n points et n droites, trois points par droites et trois droites passant par chaque point) soit est réalisable, soit nécessite l'utilisation d'une seule ligne courbe dans leur représentation. Le plan de Fano est l'unique 73-configuration et la configuration de Möbius-Kantor est l'unique 83-configuration.
Graphe d'incidence (graphe de Levi)
À chaque structure d'incidence C correspond un graphe biparti appelé graphe d'incidence ou graphe de Levi de la structure. Comme tout graphe biparti est bicoloriable, les sommets d'un graphe de Levi peuvet être colorés en noir et blanc par exemple, les sommets noirs correspondant aux points et les sommets blancs correspondant aux droites de C. Les arêtes de ce graphe correspondent aux drapeaux (paires incidentes point—droite ) de la structure d'incidence. Le graphe de Levi original est le graphe d'incidence du quadrilatère généralisé d'ordre deux (exemple 3 ci-dessus) mais le terme a été étendu par H. S. M. Coxeter pour désigner le graphe d'incidence de toute structure d'incidence[9].
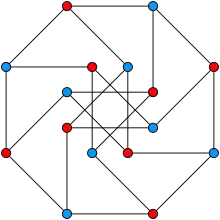
Exemples de graphes de Levi
Le graphe de Levi du plan de Fano est le graphe de Heawood. Ce graphe est connexe et sommet-transitif, et il existe un automorphisme (tel que celui défini par la réflexion autour de l'axe vertical dans la figure du graphe de Heawood) qui échange des sommets noirs et blancs. Ceci montre que le plan de Fano est auto-dual.
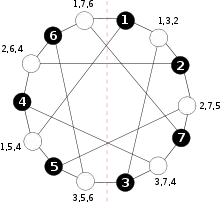
La représentation particulière du graphe de Levi de la configuration Möbius-Kantor (exemple 4 ci-dessus) illustre qu'une rotation de autour du centre (soit dans le sens horaire soit dans le sens antihoraire) du diagramme échange les sommets bleu et rouge et envoie les arêtes sur les arêtes. Autrement dit, il existe un automorphisme de ce graphe qui échange les couleurs. Par conséquent, la structure d'incidence connue sous le nom de configuration Möbius-Kantor est auto-duale.
Généralisation
On peut généraliser la notion de structure d'incidence pour inclure plus de deux types d'objets. Une structure avec k types d'objets est appelée une structure d'incidence de rang k ou une géométrie de rang k[9]. Formellement, elles sont définis comme k + 1-tuples S = (P1, P2, ..., Pk, I) avec Pi ∩ Pj = ∅ et
Le graphe de Levi pour ces structures est défini comme un graphe multipartite dont les sommets correspondant à chaque type sont colorés de la même manière.
Notes et références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Incidence structure » (voir la liste des auteurs).
- Colbourn et Dinitz 2007, p. 702
- Dembowski 1968, p. 1-2.
- Biliotti, Jha et Johnson 2001, p. 508.
- Moorhouse 2007, p. 5.
- L'autre indexation qui indexe les lignes par les droites et les colonnes par les points et aussi fréquente.
- Beth, Jungnickel et Lenz 1986, p. 17.
- Pisanski et Servatius 2013, p. 222.
- Ernst Steinitz, « Über die Construction der Configurationen n3 » , Dissertation, Breslau, 1894.
- Pisanski et Servatius 2013, p. 158
Bibliographie
- Thomas Beth, Dieter Jungnickel et Hanfried Lenz, Design Theory, Cambridge University Press, (ISBN 3-411-01675-2, lire en ligne
 )
)
- Mauro Biliotti, Vikram Jha et Norman L. Johnson, Foundations of Translation Planes, Marcel Dekker, (ISBN 0-8247-0609-9)
- Charles J. Colbourn et Jeffrey H. Dinitz, Handbook of Combinatorial Designs, Boca Raton, Chapman & Hall / CRC, , 2e éd., 1016 p. (ISBN 978-1-58488-506-1 et 1-58488-506-8, lire en ligne).

- Peter Dembowski, Finite geometries, Berlin, New York, Springer-Verlag, coll. « Ergebnisse der Mathematik und ihrer Grenzgebiete » (no 44), (ISBN 3-540-61786-8, MR 0233275, lire en ligne
 ).
). 
- G. Eric Moorhouse, « Incidence Geometry », sur University of California, University of Wyoming, (consulté le ).
- Tomaž Pisanski et Brigitte Servatius, Configurations from a Graphical Viewpoint, Springer--Verlag, (ISBN 978-0-8176-8363-4, DOI 10.1007/978-0-8176-8364-1)
- Kenneth H. Rosen (éditeur), Handbook of Discrete and Combinatorial Mathematics, Boca Raton/London/New York, CRC Press, , 1232 p. (ISBN 0-8493-0149-1), « (Chapitre 12.2) ».
- Harold L. Dorwart, The Geometry of Incidence, Prentice Hall, , 156 p. (ISBN 978-2701125398).
- Henri Lombardi, Géométries élémentaires, Tome I, Presses universitaires de Franche-Comté, 292 p. (ISBN 978-2-913322-45-5, présentation en ligne, lire en ligne).





