Manœuvre orbitale
Dans le domaine des vols spatiaux, une manœuvre orbitale est définie comme étant l’utilisation d’un système de propulsion spatiale afin de modifier l’orbite d’un astronef. Par exemple il peut s’agir de l’augmentation ou la diminution de la vitesse d’une sonde interplanétaire, de l’orientation d’un satellite, ou encore de la modification de l’inclinaison de son orbite.
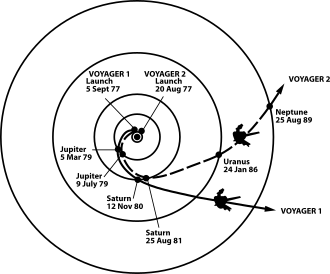
Par opposition, lorsque le véhicule spatial considéré n’est pas soumis à une manœuvre orbitale, on dit alors qu’il est en phase de vol balistique. C’est-à-dire que les seules forces majeures qu’il subit sont celles due à l’attraction gravitationnelle des corps célestes qui l’entourent.
Généralités
Équation de Tsiolkovski
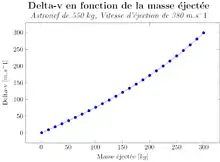
L'équation de Tsiolkovski est l'équation fondamentale de l'astronautique reliant la différence de vitesse entre le début et la fin d'une phase de propulsion d'un véhicule spatial, appelé delta-v, à la vitesse d’éjection des gaz du moteur-fusée et au rapport de la masse initiale à la masse finale de l’astronef.
Pour chacune des manœuvres orbitales, on peut appliquer l’équation de Tsiolkovski :
où :
- v est la variation de vitesse entre le début et la fin de la phase propulsée considérée ;
- est la vitesse d'éjection des gaz;
- mi est la masse totale de l'astronef au début de la phase propulsée (i pour initial) ;
- mf est la masse totale de l'astronef à l'issue de la phase propulsée (f pour final), exprimée dans la même unité que mi ;
- me est la masse d’ergols brûlés lors de la phase propulsée, exprimée dans la même unité que mi ;
- est la fonction logarithme népérien.
Budget delta-v
L’équation de Tsiolkovski relie le delta-v nécessaire à chaque manœuvre orbitale avec la quantité d’ergols nécessaire pour l’effectuer. Ainsi la somme des delta-v calculée lors de la conception du véhicule spatial en fonction de sa mission renseigne sur la quantité de carburant et comburant à prévoir. Ceci permet de ne pas être à court d’ergols durant la mission, sous peine de ne plus pouvoir contrôler le véhicule, ou à l’inverse de n’emporter que ce dont le véhicule spatial aura besoin. La somme des delta-v est appelé le budget delta-v. Une marge est généralement ajoutée au budget afin d’avoir une petite ressource d’ergols disponible en cas d’imprévus.
| Opération | Delta-V en m/s [1] |
|---|---|
| Lancement en orbite terrestre basse | Dispensé par le lanceur |
| Injection sur une orbite de transfert Terre-Lune | 3160 |
| Insertion en orbite lunaire | 900 |
| Premier transfert vers une orbite plus basse | 30 |
| Second transfert vers une orbite plus basse | 70 |
| Atterrissage sur la Lune | 2060 |
| Décollage de la Lune | 1850 |
| Injection sur une orbite de transfert Lune-Terre | 1000 |
Type de manœuvres
Manœuvre impulsive

Toute phase de propulsion a une certaine durée. Néanmoins lorsque celle-ci est très petite devant la durée de la mission, on la modélise mathématiquement par une manœuvre impulsive de durée nulle. C’est-à-dire que l’on considère que le changement du vecteur vitesse, en norme ou en direction, est instantané.
Bien qu’étant physiquement impossible due au caractère instantanée de l’impulsion, cette modélisation théorique décrit très bien les effets sur la trajectoire du véhicule spatial considéré. L’erreur de trajectoire, illustrée sur la figure ci-contre, est faible et suffisamment localisée pour être négligée à l’échelle de la trajectoire globale.
Lors des premières phases de la conception d’une mission spatiale, les différentes trajectoires envisageables d’une sonde spatiale ou d’un satellite peuvent être modélisées en utilisant l’approximation des manœuvres impulsives afin de diminuer la complexité des calculs et accélérer le processus de conception.
Longue propulsion de faible poussée
Lorsque la phase de propulsion n’est pas négligeable devant la durée de la mission, la manœuvre est dite non-impulsive. C’est souvent le cas lors de l’utilisation d’une propulsion électrique ou nucléaire. Dans ce cas, une modélisation détaillée de l’engin spatial et toutes les forces qui agissent sur celui-ci est indispensable lors de la conception et de la planification de mission.
Manœuvres lors d’assistance gravitationnelles
L'assistance gravitationnelle est l'utilisation volontaire de l'attraction d'un corps céleste pour modifier en direction et en vitesse la trajectoire d'un engin spatial. L'objectif est d'utiliser ce phénomène pour économiser les ergols qui auraient dû être consommés par le système de propulsion du véhicule pour obtenir le même résultat. Cependant cette manœuvre peut être combiné avec l’allumage d’un moteur-fusée afin d’augmenter l’effet de l’assistance gravitationnelle.
L’efficacité de cette manœuvre s’appuie sur l’effet Oberth. Celui-ci est basé sur un aspect énergétique du fonctionnement d’un moteur-fusée. En effet celui-ci transforme l’énergie chimique stockée dans les ergols en énergie cinétique. Les ergols réagissent chimiquement et sont expulsés à haute vitesse. Lors du passage à proximité d’un corps céleste, l’énergie cinétique des ergols augmente en même temps que la vitesse de l’astronef qui les contient. Ainsi il devient plus profitable d’utiliser les ergols pour une phase de propulsion à cet instant.
Cet effet est d’autant plus efficace que le débit massique du système de propulsion est important, c’est pourquoi il est principalement utilisé par des moteurs-fusées à propulsion chimique. L’efficacité de l'effet Oberth est insignifiante dans le cas d’une propulsion ionique car le débit massique est beaucoup trop faible.
Contrôle d’attitude
Lors de diverses opérations, un engin spatial peut être amené à devoir modifier son attitude, c’est-à-dire son orientation. Par exemple une sonde qui passe au-dessus d’une planète peut s’orienter de manière à photographier un point particulier, ou un satellite qui a besoin de recharger ses batteries devra positionner ses panneaux solaires face au Soleil. Ces manœuvres de faible amplitude nécessitent l’intervention régulière d’un système de contrôle d'attitude.
Lors de l’utilisation de mini-tuyères pour le contrôle d’attitude, chaque allumage consomme un peu d’ergols. Bien que la quantité consommée à chaque fois soit faible, la somme de toutes ces manœuvres sur la durée totale d’une mission est importante. Cette catégorie de manœuvres est généralement décrite dans une section dédiée au contrôle d’attitude dans un budget de delta-v.
Modification d’orbite
Il existe différentes types de manœuvres orbitales qui ont pour but de modifier l’orbite d’un engin spatial. Certaines modifient les distances caractéristiques telle que le grand axe. Et d’autres modifient seulement l’inclinaison de l’orbite. Une manœuvre orbitale complexe peut combiner les deux pour modifier l’inclinaison en même temps que la taille de l’orbite.
Transfert de Hohmann
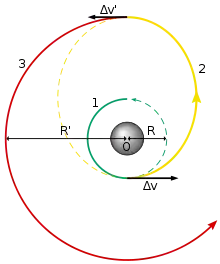
Une orbite de transfert de Hohmann est une trajectoire qui permet de passer d'une orbite circulaire à une autre orbite circulaire située dans le même plan, en utilisant uniquement deux manœuvres impulsionnelles. Cette trajectoire est celle qui consomme le moins d’énergie si l'on se limite à des trajectoires de transfert utilisant uniquement deux manœuvres.
C’est le type d’orbite souvent utilisé par le dernier étage d’une fusée lors du transfert d’un satellite vers l’orbite géostationnaire. Les dimensions de l’ellipse suivie lors du transfert sont délimitées par l’orbite de départ et celle d’arrivée.
Transfert bi-elliptique
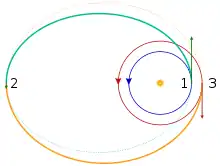
Une orbite de transfert bi-elliptique est une trajectoire qui permet de passer d’une orbite circulaire à une autre orbite circulaire située dans le même plan. Contrairement à un transfert de Hohmann, cette méthode-ci nécessite trois impulsions.
La trajectoire décrite est composée de deux demi-ellipses. Les périgées de chaque ellipse sont définis par les orbites de départ et d’arrivée. Et les apogées sont les mêmes. Les deux premières impulsions sont colinéaires au vecteur vitesse de l’astronef et dans le même sens que celui-ci ; la troisième est aussi colinéaire mais dans le sens opposé.
Bien que nécessitant une impulsion de plus qu’un transfert de Hohmann ainsi qu’un temps de transfert plus long, cette méthode peut diminuer le delta-v nécessaire dans les cas où le ratio entre les grands axes des orbites de départ et d’arrivée est égal ou supérieur à 11.94[2]. Historiquement la première formulation de cette méthode de transfert a été publiée par Ary Sternfeld en 1934[3].
Transfert de faible énergie

Une orbite de transfert à basse énergie (en) est une trajectoire qui permet de réduire le delta-v de l’ordre de 10 à 25 % comparée avec les autres méthodes de transfert, mais nécessite bien plus de temps et une poussée longue et continue[4] - [5]. C’est généralement la méthode utilisée dans le cas d’une propulsion électrique ou nucléaire.
L’avantage d’un tel transfert est la réduction importante de la masse d’ergols nécessaire et donc la possibilité d’emporter plus d’instruments scientifiques pour la mission. En contrepartie les durées des transferts sont généralement plus longues que pour une injection directe. De plus les trajectoires, étant généralement le résultat d’optimisations entre les forces de gravitations qui agissent sur l’astronef, elles sont soumises à une certaine instabilité. Ceci peut amener à une capture gravitationnelle non-désirée, une mise en orbite ou un choc avec la surface de l’astronef par un corps lors d’un survol trop rapproché.
L’illustration ci-contre représente l’une des trajectoires des sondes GRAIL dans le référentiel géocentré tournant dans lequel le Soleil est fixe. La seconde sonde a suivi une trajectoire différente, mais très proche de celle-ci, afin d’être en bonne position pour la mission. Les sondes GRAIL ont rejoint la Lune en 4 mois alors que les missions Apollo ne mettaient que 3 jours[6].
Changement d’inclinaison
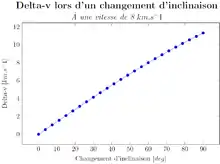
Un changement d’inclinaison nécessite qu’une seule impulsion, et modifie seulement l’inclinaison de l’orbite du véhicule spatial. Lors d’une manœuvre de changement d’inclinaison le delta-v nécessaire est égal à :
où :
- est la variation de vitesse entre le début et la fin de la phase propulsée considérée ;
- est la norme de la vitesse de l’astronef au début de la phase propulsée ;
- est la variation d’inclinaison désirée ;
- est la fonction sinus.
Malgré l’unique impulsion, le bilan en delta-v peut être rapidement très important et cette manœuvre est le plus possible évitée lors de la conception de mission. C’est une des raisons pour lesquelles il est plus intéressant, du point de vue du delta-v, de lancer un satellite géostationnaire à l’aide d’un lanceur qui décollerait proche de l’équateur. En effet une fusée décollant d’une latitude non nulle devra irrémédiablement effectuer un changement d’inclinaison durant sa trajectoire. La variation d’inclinaison devra être égale à la latitude de son point de lancement.
Afin de minimiser le delta-v nécessaire, une manœuvre de changement d’inclinaison doit se faire lorsque la vitesse de l’astronef est la plus petite. C’est pourquoi cette manœuvre est généralement effectuée à l’apocentre de l’orbite, lorsque la vitesse orbitale est minimale.
Il peut également être plus efficace, du point de vue du delta-v, d’augmenter les dimensions de l’orbite d’un satellite, ce qui a pour effet de diminuer sa vitesse orbitale, puis d’effectuer un changement d’inclinaison avant de revenir sur son orbite initiale. Bien que cette méthode nécessite trois manœuvres, l’avantage d’effectuer le changement d’inclinaison sur une orbite haute, et donc à faible vitesse, supplante le delta-v requis par les manœuvres qui élève et diminue l’orbite[7].
Rendez-vous orbital

Un rendez-vous orbital définit une rencontre entre deux véhicules spatiaux en vue d’un contact et d’un maintien mécanique pour ne former qu’un seul objet. Un rendez-vous orbital doit s’initier par une mise en phase des deux astronefs, puis de leur amarrage. Dans certains cas, il peut y avoir un désamarrage lorsque la mission l’indique.
Un cas habituel de rendez-vous en orbite est lors de l’arrivée d’astronautes à bord d’un vaisseau Soyouz à la Station spatiale internationale.
Mise en phase
En astrodynamique, la mise en phase de deux véhicules spatiaux est l’ajustement de leur anomalies vraies afin qu’elles soient de même valeur, c’est-à-dire pour qu’ils soient à la même position en même temps.
La méthode la plus couramment utilisée est d’augmenter ou de diminuer l’orbite de l’un des astronefs à l’aide d’un transfert de Hohmann, puis de faire l’opération opposée pour retourner sur l’orbite initiale. Ainsi l’orbite finale est la même que l’orbite de départ, mais la position de l’astronef sur celle-ci, c’est-à-dire son anomalie vraie, a été modifiée.
Amarrage

L’amarrage entre deux véhicules spatiaux est le contact mécanique de leurs structures respectives. Généralement l’amarrage est effectué à faible vitesse relative, c’est-à-dire que du point de vue de l’un des véhicules, le second s’approche lentement, bien que les deux véhicules aient une grande vitesse orbitale due à leurs trajectoires.
Le contrôle de la vitesse d’approche et de l’orientation des astronefs s’effectue au moyen de petites tuyères à faible poussée. Les phases de propulsion sont généralement des impulsions de faible durée.
La Station spatiale internationale, qui effectue beaucoup de rendez-vous orbitaux lors de l’arrivée de nouveaux astronautes, ou pour recevoir divers outils scientifiques, dispose d’un bras robotique, Canadarm 2, afin de faciliter certaines opérations de rendez-vous. Celui-ci fut notamment utilisé lors de l’amarrage des capsules Dragon. À l’opposé, les vaisseaux de fret ATV effectuent un amarrage entièrement automatisé.
Désamarrage
Le désamarrage consiste en la séparation d’un véhicule spatial en deux parties indépendantes. C’est par exemple une manœuvre employée lors du départ d’astronautes de la Station spatiale internationale ou bien lors de la séparation d’une sous-partie de la charge utile d’une sonde en direction d’une planète durant le survol de celle-ci.
La manœuvre implique le même type de propulsion impulsive que pour un amarrage.
Références
- « Space Manouvers », sur alternatewars.com via Wikiwix (consulté le ).
- (en) David Anthony Vallado, Fundamentals of Astrodynamics and Applications, Springer, (ISBN 0-7923-6903-3, lire en ligne), p. 317
- Sternfeld A., Sur les trajectoires permettant d'approcher d'un corps attractif central à partir d'une orbite képlérienne donnée. - Comptes rendus de l'Académie des sciences (Paris), vol. 198, p. 711-713.
- (en) Edward Belbruno, Capture Dynamics and Chaotic Motions in Celestial Mechanics: With Applications to the Construction of Low Energy Transfers, Princeton University Press, , 224 p. (ISBN 978-0-691-09480-9, lire en ligne)
- (en) Edward Belbruno, Fly Me to the Moon: An Insider's Guide to the New Science of Space Travel, Princeton University Press, , 176 p. (ISBN 978-0-691-12822-1, lire en ligne)
- « Spacecraft », sur NASA, Brian Dunbar (consulté le ).
- (en) Robert A Braeunig, « Basics of Space Flight: Orbital Mechanics »
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Orbital maneuver » (voir la liste des auteurs).
Bibliographie
- (en) George P Sutton et Oscar Biblarz, Rocket Propulsion Elements 8e édition, Wiley, (ISBN 978-0-470-08024-5)
- J. Laurent-Varin (CNES), Activité R&T à la direction des lanceurs en optimisation de la trajectoire, (lire en ligne)Présentation powerpoint sur l'optimisation de la trajectoire d'un lanceur
- R. Frank O'Brien et W. David Woods, « Le Rendez-vous en orbite lunaire : Description de la technique du rendez vous en orbite lunaire appliqué au programme Apollo (traduction de l'anglais) »,








