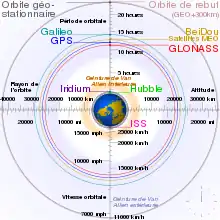
Vitesse orbitale

La vitesse orbitale d'un objet céleste, le plus souvent une planète, un satellite naturel, un satellite artificiel ou une étoile binaire, est la vitesse à laquelle il orbite autour du barycentre d'un système à deux corps, soit donc le plus souvent autour d'un corps plus massif. L'expression peut être employée pour désigner la vitesse orbitale moyenne du corps le long de son orbite ou la vitesse orbitale instantanée, en un point précis. On l'exprime en principe en m/s, mais souvent en km/h.

Comparaisons de vitesses orbitales de différents satellites de la Terre.

Vitesse orbitale instantanée

La vitesse orbitale instantanée peut être déterminée par la seconde loi de Kepler, à savoir qu'en une durée déterminée, le segment de droite reliant le barycentre au corps décrit une surface constante, quelle que soit la portion de l'orbite que le corps parcourt pendant cette durée. En conséquence, le corps va plus vite près de son périastre que de son apoastre.

Cas général

La vitesse orbitale est liée à l'équation de la force vive.

La vitesse orbitale est obtenue par :

v_{o}={\sqrt {2\left({\mu  \over {r}}+{\varepsilon }\right)}}

où :

$\mu$ est le paramètre gravitationnel standard ;
$r$ est la distance entre le corps en orbite et le centre de l'orbite ;
$\varepsilon$ est l'énergie orbitale spécifique.

Cas de l'orbite elliptique

Lorsque l'énergie orbitale spécifique est négative, l'orbite du corps secondaire est elliptique et sa vitesse orbitale est obtenue par :

v_{o}={\sqrt {\mu \left({2 \over {r}}-{1 \over {a}}\right)}}

où :

$\mu$ est le paramètre gravitationnel standard ;
$r$ est la distance entre le corps secondaire et le corps principal ;
$a$ est le demi-grand axe de l'orbite du corps secondaire.

Lorsque le corps secondaire est au périastre, la valeur de $r$ , notée $r_{\mathrm {per} }$ , est obtenue par $r_{\mathrm {per} }=a(1-e)$ , où $a$ et $e$ sont le demi-grand axe et l'excentricité de l'orbite du corps secondaire. La vitesse orbitale du corps secondaire au périastre, notée $v_{\mathrm {per} }$ , est obtenue par :

v_{\mathrm {per} }={\sqrt {\frac {\mu (1+e)}{a(1-e)}}}

Lorsque le corps secondaire est à l'apoastre, la valeur de $r$ , notée $r_{\mathrm {ap} }$ , est obtenue par $r_{\mathrm {ap} }=a(1+e)$ , où $a$ et $e$ sont le demi-grand axe et l'excentricité de l'orbite du corps secondaire. La vitesse orbitale du corps secondaire à l'apoastre, notée $v_{\mathrm {ap} }$ , est obtenue par :

v_{\mathrm {ap} }={\sqrt {\frac {\mu (1-e)}{a(1+e)}}}

Cas de l'orbite circulaire

Une orbite circulaire est, par définition, une orbite dont l'excentricité est nulle.

La vitesse orbitale du corps secondaire en orbite circulaire est obtenue par :

v_{o}={\sqrt {\mu  \over {r}}}

où :

$\mu$ est le paramètre gravitationnel standard ;
$r$ est la distance entre le corps secondaire et le corps principal.

Cas de la trajectoire parabolique

Lorsque l'énergie orbitale spécifique est nulle, la trajectoire du corps secondaire est parabolique et sa vitesse orbitale est obtenue par :

v_{o}={\sqrt {\mu \left({2 \over {r}}\right)}}

où :

$\mu$ est le paramètre gravitationnel standard ;
$r$ est la distance entre le corps secondaire et le corps principal.

Cas de la trajectoire hyperbolique

Lorsque l'énergie orbitale spécifique est positive, la trajectoire du corps secondaire est hyperbolique et sa vitesse orbitale est obtenue par :

v_{o}={\sqrt {\mu \left({2 \over {r}}+{1 \over {a}}\right)}}

où :

$\mu$ est le paramètre gravitationnel standard ;
$r$ est la distance entre le corps secondaire et le corps principal ;
$a$ est le demi-grand axe de l'orbite du corps secondaire.

Vecteur vitesse instantanée

Dans le cas d’une orbite elliptique, on s’intéresse au vecteur vitesse tel qu’il s’exprime dans le référentiel (non galiléen) fixé sur le corps central, en choisissant l’axe Ox qui pointe en direction du périastre (Ox est donc parallèle au grand axe et dirigé vers le point le plus proche de l’orbite).

La position et la vitesse vectorielles sont des conditions initiales nécessaires à l’intégration de la relation fondamentale de la dynamique.

En connaissant à un instant donné la position ${\vec {r}}=(r_{x},r_{y})$ du corps sur son orbite, il s’agit de déterminer le vecteur vitesse correspondant ${\vec {v}}=(v_{x},v_{y})$ .

Au périastre ou à l’apoastre, la solution est simple car le vecteur vitesse est orthogonal au vecteur position en ces points.

Les relations suivantes sont plus générales :

v_{x}=-{\frac {a}{r}}{\frac {1}{\sqrt {1-e^{2}}}}\ r_{y}\ {\dot {M}}

v_{y}={\frac {a}{r}}{\sqrt {1-e^{2}}}\ (r_{x}+a\ e)\ {\dot {M}}

où ${\dot {M}}$ est la dérivée de l’anomalie moyenne par rapport au temps, soit le mouvement moyen :

{\dot {M}}={\sqrt {\frac {G(m_{1}+m_{2})}{a^{3}}}}

Remarque :

Lorsque la masse orbitale $m_{2}$ $m_{2}$ n’est pas négligeable par rapport à la masse centrale $m_{1}$ $m_1$ , les vecteurs position ${\vec {r}}$ $\vec r$ et vitesse ${\vec {v}}$ ${\vec v}$ devraient être représentés dans le référentiel inertiel fixé au barycentre. Les relations précédentes restent toutefois valables :
- Ces vecteurs vus du barycentre (ainsi que $a$ ) sont proportionnels aux vecteurs vus de la masse centrale avec un rapport multiplicatif $m_{1}/(m_{1}+m_{2})$ , et les équations sont homogènes.
- Par contre, puisque l’anomalie moyenne $M$ ne change pas, le $a$ intervenant dans sa définition reste le demi-grand axe de l’ellipse dont le foyer est le corps central.

Preuve

Selon la définition de l’anomalie vraie notée $\nu$ , on peut exprimer le vecteur position par

r_{x}=r\cos(\nu )

r_{y}=r\ sin(\nu )

D’autre part, l’anomalie vraie est liée à l’anomalie excentrique notée $E$ par les relations

\cos(\nu )={\frac {a}{r}}(\cos(E)-e)

\ sin(\nu )={\frac {a}{r}}{\sqrt {1-e^{2}}}\sin(E)

où $E$ et le rayon $r$ sont liés par

r=a\ (1-e\cos(E))

On peut alors exprimer la position à l’aide de l’anomalie excentrique

r_{x}=a\ (\cos(E)-e)

r_{y}=a\ {\sqrt {1-e^{2}}}\ \sin(E)

puis dériver ces relations par rapport au temps pour obtenir la vitesse

v_{x}=-a\ \sin(E)\ {\dot {E}}

v_{y}=a\ {\sqrt {1-e^{2}}}\cos(E)\ {\dot {E}}

Il s’agit maintenant de s’abstraire de $E$ qui est lié à l’anomalie moyenne notée $M$ , conformément à l’équation de kepler :

E-e\cdot \sin(E)=M

et dont la dérivée temporelle s’écrit

(1-e\cdot \cos(E))\ {\dot {E}}={\dot {M}}

ou encore

{\dot {E}}={\frac {a}{r}}\ {\dot {M}}

Pour conclure, il suffit de substituer $\sin(E)$ et $\cos(E)$ tirés respectivement des relations sur $r_{x}$ et $r_{y}$ pour les introduire dans les relations sur $v_{x}$ et $v_{y}$ .

Un peu de calcul permet par ailleurs de retrouver l’expression du module de la vitesse indiquée plus haut :

v_{o}=\|{\vec {v}}\|={\sqrt {\mu \left({2 \over {r}}-{1 \over {a}}\right)}}

Vitesse orbitale moyenne

Cas d’une orbite circulaire

La vitesse orbitale moyenne est déterminée soit en connaissant sa période orbitale et le demi-grand axe de son orbite, soit à partir des masses des deux corps et du demi-grand axe (qui est ici le rayon du cercle) :

v_{o}={2\pi a \over T}

v_{o}={\sqrt {MG \over r}}

où v_o est la vitesse orbitale moyenne, a est la longueur du demi-grand axe, r est le rayon du cercle de l’orbite (= a), T est la période orbitale, M est la masse du corps autour duquel orbite celui dont on veut calculer la vitesse et G est la constante gravitationnelle. Dans la seconde relation, on reconnaît le rapport entre la circonférence du cercle de l’orbite et le temps de parcours. Ceci n'est qu'une approximation qui est vérifiée lorsque la masse du corps orbitant est considérablement plus faible que celle du corps central.

Lorsque la masse du corps orbitant n'est pas négligeable devant celle de l'autre corps, il s’agit de prendre en compte le fait que les deux corps se déplacent l’un et l’autre sur leurs orbites circulaires respectives. Dans ce cas, la vitesse moyenne recherchée est celle mesurée depuis le référentiel galiléen fixé au barycentre. Elle est donnée par la relation :

v_{o}={\sqrt {m_{1}^{2}\ G \over (m_{1}+m_{2})\ r}}

où m₁ est la masse du corps central, m₂ celle du corps considéré, et r le rayon entre les deux corps. Il s'agit ici encore du cas particulier où les orbites des deux corps sont circulaires.

Preuve

Soit $r$ la distance entre les deux corps et $R$ la distance entre le corps considéré et le barycentre. Il s’agit d’évaluer la vitesse moyenne définie par

v_{o}={2\pi R \over T}

Dans le problème à deux corps, il est montré que

R={\frac {m_{1}}{m_{1}+m_{2}}}\ r

Exploitant la 3ème loi de Kepler, Isaac Newton a montré la relation

T^{2}={\frac {4\pi ^{2}a^{3}}{G(m_{1}+m_{2})}}

dans laquelle $a$ est ici égal à $r$ .

On obtient le résultat en substituant $T$ tiré de cette dernière relation.

Cas d’une orbite elliptique

Dans ce cas, il suffit de déterminer le périmètre $L$ (ou la circonférence) de l’ellipse, mais on ne peut pas l’exprimer par des fonctions simples ; il convient d’exploiter la fonction intégrale elliptique de deuxième espèce. Il existe toutefois des approximations ; la première (due à Kepler) indique une valeur par défaut et la seconde (due à Euler) donne une valeur par excès :

2\pi {\sqrt {ab}}\leq L\leq \pi {\sqrt {2(a^{2}+b^{2})}}

a et b étant respectivement les deux demi-axes de l’ellipse qui sont liés à l’excentricité e par la relation $b=a{\sqrt {1-e^{2}}}$ . On en déduit

{\frac {m_{1}^{2}\ G\ {\sqrt {1-e^{2}}}}{(m_{1}+m_{2})\ a}}\leq v_{o}^{2}\leq {\frac {m_{1}^{2}\ G(1-e^{2}/2)}{(m_{1}+m_{2})\ a}}

Remarques :

Ces expressions concernent la vitesse mesurée depuis le référentiel fixé au barycentre.
L’écart relatif entre les bornes respectives reste inférieur à $10^{-5}$ tant que e est inférieur à 0.1.
On obtiendra une estimation plus précise en prenant la moyenne des racines des deux bornes.

Exemple de paradoxe

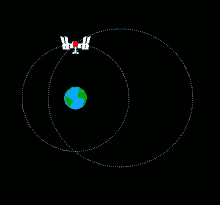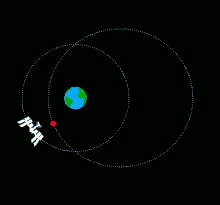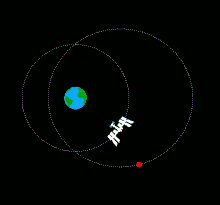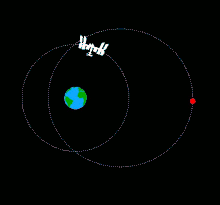
Animation de l'envoi d'une balle en direction de la terre depuis la station spatiale internationale. Le mouvement de la balle vu depuis la station est contre intuitif. La balle commence à descendre vers la Terre comme on pourrait s'y attendre puis elle s'arrête et repart dans l'autre sens et dépasse l'orbite de la station.

Une balle lancée manuellement en direction de la Terre depuis la Station spatiale internationale (ISS) aura quasiment la même vitesse que la station spatiale, c'est-à-dire de plus de sept kilomètres par seconde et quasi parallèle à la surface terrestre. La balle suivra une orbite très proche de celle de la station, à peine plus elliptique. La balle se rapprochera de la Terre dans un premier temps en raison de la modification de son orbite, puis s'en éloignera et, au bout d'une demi-orbite, croisera celle de l'ISS. Au bout d'une orbite entière, la balle rejoindra en théorie la station spatiale. La balle ne tombera donc pas sur la Terre[1].

Notes et références

(en) « Why A Ball Thrown To Earth From Orbit "Boomerangs". Can Astronauts Hit Earth With A Ball, Arrow Or Bullet? | Science 2.0 », sur www.science20.com, 2 décembre 2015 (consulté le 5 août 2020).

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.