Méthode de Oberst
La méthode de Oberst[1] est utilisée en vibroacoustique pour l'étude et la mesure des propriétés mécaniques de matériaux amortissants solides. Elle consiste à faire vibrer une poutre métallique revêtue de matériau amortissant et encastrée (type cantilever).
L'emploi de matériaux amortissants tend à se développer pour répondre à des normes et réglementations plus exigeantes que par le passé. De nombreux secteurs sont concernés : transports, construction, électroménager, etc. Par exemple, les concepteurs de moteurs, de véhicules ou d'édifices sont amenés à les rendre de plus en plus silencieux.
La caractérisation des matériaux amortissants vibratoires selon la méthode de test de la poutre de Oberst est particulièrement utilisée dans l'industrie automobile.
Le bruit dans les véhicules fait depuis les années 2000 l'objet d'études sérieuses chez les constructeurs. Les acousticiens estiment que l'on gagne trois décibels pour chaque type de bruit émis par un véhicule[2], tous les dix ans environ.
Principe
On utilise une éprouvette ayant la forme d'une poutre, composée d'une tôle support (généralement en acier) connue qui est revêtue sur une face d'un échantillon de matériau amortissant (ou viscoélastique) à tester. Cette poutre composite est fixée sur un support en acier inoxydable amagnétique par un système à simple encastrement, cas le plus courant.
L'essai mécanique consiste à soumettre cette « poutre de Oberst » à une excitation (en bruit blanc) forcée à l'aide d'un champ magnétique sur les modes de vibration 2 et 3[3]. Un capteur sans contact mesure les vitesses de déplacement de la poutre. Le signal temporel est ensuite discrétisé et transformé en signal fréquentiel à l'aide d'un analyseur de spectre à FFT. Le spectre obtenu représente la courbe de la vitesse en fonction de la fréquence.
Au préalable, il faut tester la poutre de base en acier (sans matériau appliqué) qui servira de substrat. Ce dernier a significativement une plus grande rigidité et de plus faibles propriétés amortissantes que le matériau.
Flexion simple d'une poutre uniforme
Considérons le cas le plus élémentaire, celui de la poutre uniforme (poutre de base, constituée d'un seul matériau). Sous l'effet d'une excitation, la théorie prédit que les différentes fréquences propres (ou de résonance) en flexion simple d'une poutre uniforme, correspondant aux différents modes de vibration, sont fonction :
- du type de conditions aux limites (« encastré-libre », « encastré-encastré », etc.) ;
- des propriétés physiques du matériau de la poutre : module de Young et masse volumique ;
- et de sa géométrie : moment d'inertie de la section par rapport à l'axe de flexion, aire de la section droite et longueur.
Cette méthode permet de mesurer le module d'un matériau.

Pour une poutre de section rectangulaire, l'équation est[4] - [5] :
avec :
- E, le module de Young du matériau de la poutre (qui dépend de la température T), en Pa ;
- n, l'indice qui renvoie le numéro d'ordre de la vibration de résonance : 1, 2, 3, etc. ;
- fn, la fréquence de résonance pour le mode n, en Hz ;
- L, la longueur libre de la poutre, en m ;
- ρ, la masse volumique de la poutre, en kg/m3 ;
- e, l'épaisseur de la poutre suivant la direction de vibration, en m ;
- Cn, un coefficient relatif au mode n et dépendant du type de conditions aux limites. Pour une poutre « encastré-libre »[6], les premières valeurs sont[4] :
- C1 = 0,55959,
- C2 = 3,5069,
- C3 = 9,8194,
- C4 = 19,242,
- C5 = 31,809,
- et Cn = (π/2)(n-0,5)2, pour n>3.
Remarque : le module de Young est lié à la célérité cL des ondes longitudinales dans un solide par la relation E = ρ cL2.
Poutre composite
Dans le cas d'une poutre composite (c'est-à-dire tôle support avec matériau), l'analyse spectrale de fréquences propres en flexion permet de déterminer directement la valeur du facteur d'amortissement global (ou « valeur de Oberst »), à une température donnée. Pour cela, on utilise la méthode de la largeur de la bande de fréquence à −3 dB de la valeur maximale d'un pic de résonance.
Le facteur d'amortissement (ou de perte) η (sans unité) d'un matériau traduit sa capacité à diminuer les amplitudes de vibrations solidiennes ; il mesure aussi son aptitude à dissiper l'énergie mécanique en chaleur.
La méthode vibratoire de Oberst permet de connaître indirectement le facteur d'amortissement et le module de Young complexe intrinsèques du matériau à une seule couche rapporté sur le support, à partir des mesures réalisées avec la poutre de référence en tôle.
Remarque : le facteur de perte global ne peut pas être supérieur au facteur de perte intrinsèque du matériau amortissant.
Système de mesure
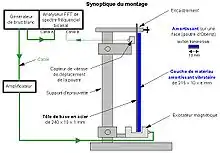

Les fixations de l'excitateur et du capteur sont ajustables pour optimiser les réglages.
Le « montage de Oberst » (support plus éprouvette) est conditionné dans une chambre d'essai (réglable par exemple de −30 à 60 °C) à la température de l'essai.
Il est ainsi possible de déterminer les facteurs d'amortissement et les modules de Young en fonction de la fréquence (gamme typique de 10 Hz à 1 kHz) et de la température.
Exploitation des résultats d'un essai
À partir du signal d'entrée connu et de la réponse de la poutre, la fonction de réponse fréquentielle est calculée en temps réel par l'analyseur FFT pour déterminer la fréquence propre et le facteur d'amortissement de chaque mode de résonance de la poutre.
La méthode de Oberst n'est pas adaptée pour mesurer des facteurs de perte supérieurs à 20 %.
Poutre uniforme
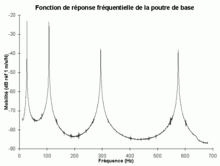
La méthode de Oberst est mentionnée par exemple dans la méthode d'essai D45 1809 des principaux constructeurs automobiles français. En pratique, cette dernière impose une épaisseur de tôle e = 10−3 m et une longueur libre (sous encastrement) L = 0,216 m.
Les fréquences de résonance à 23 °C±0,5 °C des quatre premiers modes de la poutre acier de référence sont bien connues. La comparaison de ces quatre valeurs attendues avec les valeurs mesurées constitue un moyen de vérifier le montage du système de mesure.
Poutre revêtue de matériau amortissant sur une face
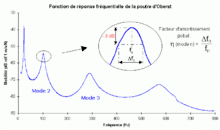
Les résultats de l'essai dépendent beaucoup du soin apporté à la préparation et à la mise en place de l'éprouvette.
En comparaison avec le spectre de la poutre de base, la forme de la courbe autour de chaque mode a changé (élargissement des pics) car le facteur de perte d'une poutre composite est typiquement cent fois supérieur à celui de l'acier.
Pour un substrat donné, le facteur d'amortissement global (ou composite) η dépend :
- de l'épaisseur e1 du matériau appliqué, si les valeurs de e1 sont modérées. En effet, pour des valeurs de e1 élevées, le facteur de perte Oberst tend presque vers la valeur du facteur de perte du matériau seul ;
- des propriétés du matériau appliqué : module de Young et facteur d'amortissement intrinsèque.
Par exemple, pour atteindre avec e1 = 3 mm une valeur de Oberst de 10 % avec un facteur d'amortissement intrinsèque de 50 %, le module de Young du matériau doit être d'environ 300 MPa.
Remarque : la densité du matériau ou celle du substrat n'a pas d'effet sur la valeur de Oberst. Cependant, un matériau plus dense réduira les niveaux de vibration et déplacera les fréquences de résonance.
L'utilisation d'abaques permet à l'expérimentateur d'ajuster les propriétés du matériau pour atteindre une valeur cible de Oberst requise dans un cahier des charges constructeur.
Notes et références
- Cette méthode (en anglais : Oberst beam test) est nommée d'après son inventeur, le Dr H. Oberst.
- Il existe trois grandes sources de bruit : en provenance du groupe motopropulseur, lié à l'aérodynamisme, et à la route.
- Les forts débattements du mode 1 peuvent affecter la qualité de la mesure.
- (en) ASTM E 756-98, Standard test method for measuring vibration-damping properties of materials, p. 7, 12 p.
- La largeur de la poutre n'intervient pas dans la formule.
- Cette configuration est appelée en anglais : clamped-free.
Voir aussi
Articles connexes
- Analyse mécanique dynamique, une méthode complémentaire qui permet de mesurer directement le facteur de perte et le module d'élasticité d'un matériau en fonction de la fréquence et de la température.
- Traitement numérique du signal
- Diapason
- Onde sur une corde vibrante
Lien externe
- (en) Paul Macioce, « Viscoelastic Damping 101 » [PDF], Roush Industries (consulté le ), 3 p. (informations générales complémentaires en physique vibratoire).
Bibliographie
- (en) A.D. Nashif, D.I.G. Jones et J.P. Henderson, Vibration Damping, John Wiley & Sons, New York, 1985 (ISBN 0-471-86772-1).
- (en) E.E. Ungar, Damping of Panels, in Noise and Vibration Control, L.L. Beranek (éd.), McGraw-Hill, New York, 1971 (ISBN 978-0-07-004841-6).
Normes
- ISO 6721-1 : Plastiques - Détermination des propriétés mécaniques dynamiques - Partie 1 : Principes généraux.
- ISO 6721-3 : Plastiques - Détermination des propriétés mécaniques dynamiques - Partie 3 : Vibration en flexion - Méthode en résonance.
- ASTM E756 : Méthode de test pour la mesure des propriétés en amortissement vibratoire de matériaux.
