Loi binomiale négative
En probabilité et en statistiques, une loi binomiale négative est la distribution de probabilité discrète du nombre d'échecs dans une série d'épreuves de Bernoulli indépendantes et identiquement distribuées jusqu'à avoir un nombre fixe n de succès. Par exemple, c'est la distribution de probabilité du nombre de piles obtenus dans une série de pile ou face jusqu'à avoir vu n faces. Plus précisément, elle décrit la situation suivante : une expérience consiste en une série de tirages indépendants, donnant un succès avec probabilité p (constante durant toute l'expérience) et un échec avec une probabilité complémentaire 1-p. Cette expérience se poursuit jusqu'à l'obtention d'un nombre donné n de succès. La variable aléatoire représentant le nombre d'échecs, avant l'obtention du nombre donné n de succès, suit alors une loi binomiale négative. Ses paramètres sont : le nombre n de succès attendus, et la probabilité p d'un succès. Le paramètre n se note parfois r, comme sur l'illustration ci-contre.
| Binomiale négative | |
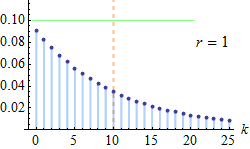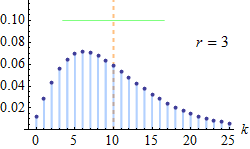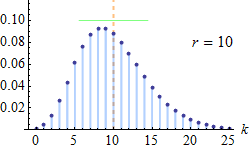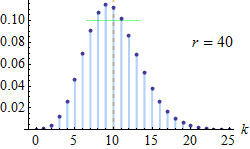 Fonction de masse pour plusieurs valeurs de n et pour une loi de moyenne 10. | |
| Paramètres | [1] |
|---|---|
| Support | |
| Fonction de masse | |
| Fonction de répartition | est la fonction bêta incomplète régularisée |
| Espérance | |
| Mode | |
| Variance | |
| Asymétrie | |
| Kurtosis normalisé | |
| Fonction génératrice des moments | |
| Fonction caractéristique | |
| Fonction génératrice des probabilités | |
La loi se généralise à deux paramètres r et p, où r peut prendre des valeurs réelles strictement positives. Cette généralisation est aussi connue sous le nom de loi de Pólya[2], en l'honneur du mathématicien George Pólya.
Définition
Définition pour un premier paramètre entier
La loi binomiale négative dépend de deux paramètres, mais plusieurs autres paramétrisations sont envisageables. Une paramétrisation très répandue introduit un entier naturel n non nul et un réel non nul[3] p compris entre 0 et 1. Il est courant d'introduire la probabilité complémentaire q = 1 – p. La fonction de masse d'une variable aléatoire distribuée selon une loi binomiale négative de paramètres n et p prend la forme suivante :
où est un coefficient binomial.
La loi binomiale négative s'interprète comme la loi de probabilité de la variable aléatoire X qui compte le nombre d'échecs observés avant l'obtention de n succès pour une série d'expériences indépendantes, sachant que la probabilité d'un succès est p. Ainsi
La fonction de masse de la binomiale négative peut aussi s'écrire sous la forme
où est un coefficient binomial généralisé à un entier négatif et est défini par.Cette expression justifie le nom de loi binomiale négative donnée à cette loi de probabilité. Elle facilite aussi, grâce à l'usage de la formule du binôme négatif, le calcul de son espérance et de sa variance .
Si une variable aléatoire X suit une loi binomiale négative de paramètres n et p on pourra alors noter[4] .
Définitions alternatives
- On trouve parfois la définition alternative suivante : la loi binomiale négative[5] de paramètres n et p, aussi appelée loi de Pascal pour la distinguer de la première définition[6], est la loi de la variable aléatoire Y comptant le nombre d'essais nécessaires avant l'obtention de n succès. AinsiLes deux fonctions de masse (pour X et pour Y) se déduisent l'une de l'autre par la substitution Y = X + n et m = k + n, ainsi
.
- La loi binomiale négative est parfois définie comme le nombre de succès observés avant l'obtention du nombre donné n d'échecs, conduisant à intervertir le rôle des paramètres p et q ainsi que les mots « succès » et « échec ».
Dans la suite, on prendra la première définition pour définir de la loi binomiale négative.
Généralisation à un premier paramètre réel
Il est possible de généraliser la définition de la loi binomiale négative à un paramètre r réel strictement positif (qui remplace alors le paramètre entier n) en utilisant des coefficients binomiaux généralisés. Plus précisément, pour r réel strictement positif et p réel non nul entre 0 et 1, la loi binomiale négative (généralisée) de paramètres r et p est la loi discrète définie par la fonction de masse
où désigne la factorielle décroissante et désigne la fonction gamma. Cette définition reste bien sûr compatible avec la définition dans le cas d'un paramétrage entier. La loi binomiale négative généralisée à un paramètre réel s'appelle parfois Loi de Pólya[2]. Dans le cadre de cette généralisation, il n'est plus possible d'interpréter la loi en termes de nombres de succès.
Propriétés
Fonction de répartition
La fonction de répartition peut s'exprimer à l'aide de la fonction bêta incomplète régularisée :
.
Une démonstration par récurrence sur k prouve que
.
Mélange de lois Gamma-Poisson
La loi binomiale négative (généralisée) avec paramètres r réel strictement positif et où θ est un réel strictement positif est égale à un mélange de lois Gamma-Poisson où r et θ sont les paramètres de la loi Gamma.
Convergence vers la loi de Poisson
Une loi binomiale négative de paramètres n et avec λ réel fixé strictement positif converge faiblement vers une loi de Poisson de paramètre λ lorsque n converge vers l'infini. En d'autres termes, si et alors on a la convergence en loi .
Lien avec la loi géométrique
Comme il existe deux définitions de la loi binomiale négative, il existe deux définitions de la loi géométrique. Si celle-ci modélise le nombre d'échecs avant le premier succès, elle correspond à la loi binomiale négative de paramètres 1 et p.
.
Si Xn est une variable aléatoire distribuée selon la loi binomiale négative de paramètres n et p, alors Xn est la somme de n variables aléatoires indépendantes distribuées selon une loi géométrique de paramètre p. Le théorème central limite indique de plus que Xn est approximativement normal, pour n suffisamment grand.
Lien avec la loi binomiale
En outre, si Yk+n est une variable aléatoire distribuée selon une loi binomiale de paramètre k + n et p, alors
La dernière ligne s'interprète ainsi : c'est la probabilité qu'après k + n épreuves, il y ait au moins n succès. Ainsi, la loi binomiale négative peut être vue comme la réciproque de la loi binomiale.
Stabilité par somme
La somme de k variables aléatoires indépendantes et distribuées selon des lois binomiales négatives de paramètres p et respectivement n1, n2,..., nk est encore une loi binomiale négative, de paramètres p et n = n1 +...+ nk. Cette propriété se démontre aisément à partir de l'expression de la fonction génératrice des moments.
Applications
Temps d'attente dans un processus de Bernoulli
Pour tout entier n, la loi binomiale négative est la distribution de succès et d'échecs dans une série d'épreuves de Bernoulli iid. Pour k + n épreuves de Bernoulli, avec probabilité de succès p, la loi binomiale négative donne la probabilité de k échecs et n succès, le dernier tirage étant un succès. Autrement dit, la loi binomiale négative est la distribution du nombre d'échecs avant le n-ième succès dans des épreuves de Bernoulli, de probabilité de succès p.
Considérons l'exemple suivant. On lance plusieurs fois un dé honnête, et la face 1 est considérée comme un succès. La probabilité de succès à chaque épreuve est 1/6. Le nombre d'épreuves nécessaires pour obtenir 3 succès appartient à l'ensemble infini { 3, 4, 5, 6, ... }. Ce nombre d'épreuves est une variable aléatoire distribuée selon une loi binomiale négative (décalée, car l'ensemble commence à 3 et pas à 0). Le nombre d'échecs avant le troisième succès appartient à l'ensemble { 0, 1, 2, 3, ... }. Ce nombre d'échecs est aussi distribuée selon une loi binomiale négative.
Loi de Poisson « sur-dispersée »
La loi binomiale négative, en particulier dans sa paramétrisation alternative décrite plus haut, est une alternative intéressante à la loi de Poisson. Elle est particulièrement utile pour des données discrètes, à valeurs dans un ensemble positif non-borné, dont la variance empirique excède la moyenne empirique. Si une Poisson est utilisée pour modéliser de telles données, la moyenne et la variance doivent être égales. Dans ce cas, les observations sont «sur-dispersées» par rapport au modèle Poisson. Puisque la loi binomiale négative possède un paramètre supplémentaire, il peut être utilisé pour ajuster la variance indépendamment de la moyenne.
Références
- La loi binomiale négative peut se généraliser à un paramètre réel strictement positif, dans ce cas on notera le paramètre r plutôt que n par souci de clarté. Pour cette généralisation toutes les formules de l'infoboite restent vraies en changeant les occurrences de n en r. Le coefficient binomial dans la fonction de masse devient alors un coefficient binomial généralisé.
- A ne pas confondre avec la loi de Markov-Pólya.
- La probabilité p ne peut être nulle car sinon il serait impossible d'observer, en temps fini, les n succès attendus. D'ailleurs on remarquera que si on substituait 0 à p dans la formule de la fonction de masse, cette dernière serait alors toujours nulle, quel que soit la valeur de k, ce qui ne conviendrait pas pour une fonction de masse dont la somme sur toutes les valeurs de k se doit de valoir 1.
- Astrid Jourdan et Célestin C Kokonendji, « Surdispersion et modèle binomial négatif généralisé », Revue de statistique appliquée, vol. 50, , p. 73-86 (lire en ligne)
- D. Ghorbanzadeh, Probabilités : exercices corrigés, Technip, (lire en ligne), p. 156.
- G. Millot, Comprendre et réaliser les tests statistiques à l'aide de R, De Boeck Supérieur, (lire en ligne), p. 269-271.
Voir aussi
Articles connexes
- Loi binomiale négative étendue
- Problème du collectionneur de vignettes
- Loi d'Erlang : analogue de la loi binomiale négative dans le cas continu.
Bibliographie
(en) Joseph M. Hilbe (en), Negative Binomial Regression, Cambridge University Press, (lire en ligne)

![{\displaystyle p\in \,]0,1]}](https://img.franco.wiki/i/4562bae519c362bc8cc503aabcc50892aaaf7c7d.svg)


















![{\displaystyle \mathbb {E} [X]={\frac {nq}{p}}}](https://img.franco.wiki/i/052e181f2ce21f28c0d86acf17baec07a0c34369.svg)



![{\displaystyle \mathbb {E} [X]=\mathbb {E} [Y]-n={\frac {n}{p}}-n={\frac {nq}{p}}{\text{ et }}\operatorname {Var} (X)=\operatorname {Var} (Y)={\frac {nq}{p^{2}}}}](https://img.franco.wiki/i/07022964705fc2866422957e7cc81095dc82b7bf.svg)






















