Problème du collectionneur de vignettes

Le problème du collectionneur de vignettes ou du collectionneur de coupons (en anglais : coupon collector's problem, CCP) est un problème de probabilités et de combinatoire qui consiste à estimer le nombre de paquets de céréales à acheter pour collectionner une série complète de vignettes, à raison d'une vignette offerte dans chaque paquet. La vignette contenue dans chaque paquet étant inconnue à l'achat, il s'agit d'un tirage avec remise. En moyenne, si la série compte $n$ vignettes différentes, il faut acheter $n (1 + 1 / 2 + 1 / 3 + ... + 1 / n)$ paquets de céréales.

Graphique qui donne, pour chaque nombre

n

de vignettes différentes (axe vertical), le nombre moyen

E (T)

de paquets de céréales à acheter pour les posséder toutes (axe horizontal).

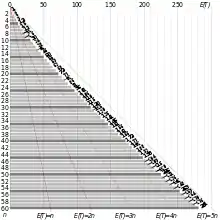
Le problème du collectionneur de vignettes était déjà mentionné en 1812 par Pierre-Simon de Laplace dans sa Théorie analytique des probabilités, où il donne, avant Erdős et Rényi, la convergence vers la loi de Gumbel. Il est aussi mentionné par George Pólya[1], et il est notamment cité par William Feller[2]. L'étude de ce problème et de ses généralisations trouve des applications notamment en ingénierie des télécommunications.

Définition et notations

L'objectif du collectionneur est de posséder une vignette pour chacun des $n$ types de vignettes. Pour cela, il achète des boîtes de céréales. Comme le montre la figure ci-dessous, il y a une vignette dans chaque boîte. Dans l'exemple, il achète sa première boîte dans laquelle il obtient la vignette 1. Il achète la deuxième boîte et on obtient la vignette 4. Dans son troisième achat, il obtient la vignette 1 à nouveau : sa collection reste donc la même, à savoir il possède la vignette 1 et 4. Il continue à acheter des boîtes de céréales jusqu'à obtenir une vignette de chaque type. On suppose que toutes les vignettes sont équiprobables : on a une probabilité de $1 / n$ d'obtenir tout type de vignettes lors de l'achat d'une boîte.

Exemple d'une collection de 4 vignettes possibles : 1, 2, 3, 4. Sur l'exemple, à l'étape 1 on obtient la vignette 1, à l'étape 2, la vignette 4. à l'étape 3, la vignette 1 à nouveau, etc.

On note $T n$ le nombre de paquets à acheter pour obtenir la collection complète. Pour l'exemple ci-dessus, $T_{4}=10$ car le collectionneur a acheté 10 boîtes de céréales avant d'obtenir les 4 vignettes. Intuitivement, les dernières vignettes sont plus difficiles à obtenir que les premières. Pour étudier ce phénomène plus précisément, on introduit également la variable aléatoire $T n,k$ que l'on note qui représente le nombre de paquets de céréales achetés avant d'obtenir $k$ types de vignettes parmi les $n$ types de vignettes de la collection. Dans l'exemple, $T_{4,1}=1$ car avec un seul achat, on possède forcément une vignette ; $T_{4,2}=2$ , $T_{4,3}=5$ et $T_{4,4}=10$ . Le temps $T n$ d'obtention de la collection totale est donc $T n,n$ . On peut considérer que $T n,k$ est un temps : à chaque pas de temps, un paquet de céréales est acheté.

Soit $t n,i$ le temps supplémentaire pour obtenir la $i$ -ème nouvelle vignette, sachant que l'on en a déjà $i - 1$ différentes. On a donc $T_{n,k}=\sum _{i=1}^{k}t_{n,i}$ . Pour l'exemple de la figure ci-dessus, on a $t_{4,1}=1$ ( $t_{n,1}$ est toujours égal à 1), $t_{4,2}=1$ , $t_{4,3}=3$ et $t_{4,4}=5$ . On a ici $T_{4}=10$ : en effet, dans l'exemple, il y a 10 boîtes achetées pour obtenir la collection complète des 4 vignettes.

Calculs de l'espérance et de la variance du temps pour finir la collection

Lorsque l'on possède déjà $i - 1$ vignettes différentes, on en trouve une nouvelle en achetant une boîte de céréales si on tombe sur l'une $n - i + 1$ vignettes nouvelles parmi les $n$ possibles. Ainsi, la probabilité d'en trouver une nouvelle est $n - i + 1 / n$ . La variable $t n,i$ suit donc une loi géométrique de paramètre $n - i + 1 / n$ . D'où l'espérance :

\mathbb {E} (t_{n,i})={\frac {1}{\text{paramètre}}}={\frac {n}{n-(i-1)}}

La variance, elle, vaut :

\mathbb {V} (t_{n,i})={\frac {1-{\text{paramètre}}}{{\text{paramètre}}^{2}}}={\frac {n(i-1)}{(n-i+1)^{2}}}={\frac {n^{2}}{(n-i+1)^{2}}}-{\frac {n}{n-i+1}}

Espérance

Par linéarité de l'espérance[3] :

{\begin{aligned}\mathbb {E} (T_{n,k})&=\mathbb {E} (t_{n,1})+\mathbb {E} (t_{n,2})+\cdots +\mathbb {E} (t_{n,k})\\&={\frac {n}{n}}+{\frac {n}{n-1}}+\cdots +{\frac {n}{n-k+1}}\\&=n\cdot \left({\frac {1}{n-k+1}}+{\frac {1}{n-k+2}}+\cdots +{\frac {1}{n}}\right)\\&=\,n\cdot (H_{n}-H_{n-k}).\end{aligned}}

Pour

n=100

vignettes à collectionner, ce graphique présente en abscisse le nombre moyen

\mathbb {E} (T_{100,k})

de paquets nécessaires pour obtenir les

k

vignettes situées en ordonnée, montrant combien les dernières vignettes sont les plus longues à obtenir.

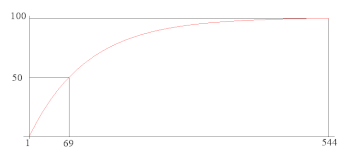
où $H_{n}=\sum _{k=1}^{n}{\frac {1}{k}}$ est le $n$ -ième nombre harmonique ( $H_{0}=0$ ) . Le temps moyen d'obtention de la collection totale est donc $\mathbb {E} (T_{n})=n\cdot H_{n}$ .

Exemples

Le collectionneur de vignettes est une métaphore et se retrouve dans des situations qui n'ont rien à voir avec des boites de céréales et des vignettes. Par exemple :

Le nombre moyen d'essais nécessaires pour obtenir la naissance d'une fille et d'un garçon est $\mathbb {E} (T_{2})=3$ . Ici, chaque naissance correspond à un tirage uniforme entre la naissance d'un garçon ou d'une fille. Le processus s'arrête lorsque l'on a "collectionné" les deux genres.
Le nombre moyen d'essais de lancers d'un dé à 6 faces pour obtenir tous les nombres de 1 à 6 est $\mathbb {E} (T_{6})=14,7$ . Ici, chaque lancer correspond à un tirage uniforme d'un nombre entre 1 et 6. Le processus s'arrête lorsque l'on a "collectionné" tous les nombres entre 1 et 6.

Comportement à l'infini

En utilisant le développement asymptotique de $H n$ , on obtient :

\mathbb {E} (T_{n})=n\cdot H_{n}=n\ln(n)+\gamma \cdot n+{\frac {1}{2}}+o(1),\ \ {\text{pour}}\ n\to \infty ,

où $\gamma \approx 0,5772156649$ est la constante d'Euler-Mascheroni.

Temps d'attente moyen de la moitié de la collection

Ce nombre est $\mathbb {E} (T_{n,n/2})=n(H_{n}-H_{n/2})=n\ln 2-{\frac {1}{2}}+o(1)$ . Ainsi, le temps d'attente moyen pour obtenir la moitié de la collection est linéaire en la taille $n$ de la collection ; il est inférieur au temps d'attente total qui est linéarithmique (voir complexité en temps).

Variance

En utilisant l'indépendance des variables $t n,i$ , on obtient[3] :

{\begin{aligned}\mathbb {V} (T_{n})&=\mathbb {V} (t_{n,1})+\mathbb {V} (t_{n,2})+\cdots +\mathbb {V} (t_{n,n})\\&={\frac {n^{2}}{n^{2}}}+{\frac {n^{2}}{(n-1)^{2}}}+\cdots +{\frac {n^{2}}{1^{2}}}-\mathbb {E} (T_{n})\\&=n^{2}\left(\sum _{k=1}^{n}{\frac {1}{k^{2}}}\right)-nH_{n}\\\end{aligned}}

En utilisant les développements asymptotiques de $H n$ et de $\sum _{k=1}^{n}{\frac {1}{k^{2}}}$ , on obtient :

\mathbb {V} (T_{n})={\frac {\pi ^{2}}{6}}n^{2}-n\ln(n)-(\gamma +1)n+o(1),\ \ {\text{pour}}\ n\to \infty .

En utilisant la valeur au point 2 de la fonction zeta de Riemann, on obtient la majoration simple :

{\begin{aligned}\mathbb {V} (T_{n})&\leqslant n^{2}\left(\sum _{k=1}^{n}{\frac {1}{k^{2}}}\right)\\&\leqslant n^{2}\left(\sum _{k=1}^{\infty }{\frac {1}{k^{2}}}\right)={\frac {\pi ^{2}}{6}}n^{2}<2n^{2}.\end{aligned}}

Un majoration simple de l’écart-type est donc $\sigma (T_{n})\leqslant {\frac {\pi }{\sqrt {6}}}n\leqslant 1,3n$ .

Estimations plus précises de l'écart à la moyenne

En utilisant l'inégalité de Bienaymé-Tchebychev , on a :

\forall \varepsilon >0,\mathbb {P} \left(|T_{n}-nH_{n}|\geqslant \varepsilon \,n\right)\leqslant {\frac {2}{\varepsilon ^{2}}}.

On peut aussi montrer le seuil suivant, en utilisant l'inégalité de Boole (union bound)[4] :

\forall \varepsilon >0,\ \lim _{n\rightarrow \infty }\mathbb {P} (T_{n}>n\ln(n)+\varepsilon n)=1-\mathrm {e} ^{-\mathrm {e} ^{-\varepsilon }}.

La première démonstration connue , via l’analyse des séries génératrices, est celle de Pierre-Simon de Laplace, dans sa Théorie analytique des probabilités en 1812[5]. On cite aussi, souvent, un article[6] - [7] d’Erdös et Rényi de 1960, où les auteurs semblent découvrir à l’occasion la loi de Gumbel, qui réapparaît dans leurs travaux la même année, dans le théorème double-exponentiel précisant le seuil de connexité des graphes aléatoires.

Avancement de la collection

On peut souhaiter calculer le nombre moyen de vignettes différentes obtenues après $N$ achats. Pour cela, on peut même supposer que les vignettes ne sont pas équiprobables, mais ont au contraire des probabilités respectives $p 1, ... , p n$ d'être trouvées à chaque achat. Dans ces conditions, après $N$ achats, le nombre moyen de vignettes différentes est $C_{N}=\sum _{k=1}^{n}\left(1-(1-p_{k})^{N}\right)$ .

Les fonctions $x\geqslant 0\mapsto x^{N}$ étant convexes, cette espérance est toujours inférieure ou égale à celle correspondant à l'équirépartition des vignettes, ce que l'intuition ne dément pas.

En outre, dans ce cas d'équiprobabilité, lorsque $N$ est proche de $n ln n$ , on trouve une valeur de $C N$ proche de $n$ , ce qui est conforme aux résultats des paragraphes précédents. Pour des vignettes mal réparties, il faudra être encore plus riche.

Généralisations

On peut généraliser le problème de plusieurs manières.

Le collectionneur a un petit frère auquel il donne les vignettes en double[8].
Le collectionneur achète des pochettes de $k$ vignettes différentes. On fait alors apparaître des coefficients binomiaux dans les formules[9].

Applications

La plupart des applications du problème du collectionneur de vignette sont des systèmes où il y a un certain nombre d'éléments à visiter et où la politique choisie est de tirer au hasard des éléments jusqu'à les avoir tous vus (au moins avec une bonne probabilité). Certains exemples sont donnés ci-dessous[10].

Certaines méthodes pour identifier les contraintes intéressantes en optimisation, consistent à faire un certain nombre de tests et à supposer qu'après cet examen on a trouvé toutes les contraintes intéressantes[11]. Le nombre de tests nécessaires est déterminé grâce aux calculs précédents.
Certains algorithmes d'optimisation ont besoin d'un point de départ, et ce point de départ influe sur le résultat obtenu, par exemple dans la recherche d'un minimum local. En utilisant plusieurs points de départ tirés au hasard on augmente la probabilité de succès en allant chercher de nouveaux minima locaux, mais on peut obtenir deux fois le même. On peut faire le parallèle avec le collectionneur de vignettes pour estimer le nombre de départs nécessaires.
Cette technique est aussi utilisée pour détecter des pannes.
Dans le domaine de la diffusion de rumeur (rumor spreading) dans un graphe, un modèle classique est celui où la rumeur est présente dans un nœud au départ et à chaque pas de temps chaque nœud informé transmet l'information à l'un de ses voisins au hasard. Le problème du collectionneur apparaît naturellement dans ce contexte.
Le problème du collectionneur de vignettes permet d'apporter un argument en faveur, mais non une preuve, de ce que le nombre π est un nombre normal. En effet si c'est bien le cas, on peut estimer le nombre de décimales à lire pour trouver les dix chiffres de 0 à 9, les cent séquences de 00 à 99 et ainsi de suite ; les estimations données par le problème du collectionneur de vignettes sont proches des valeurs obtenues en observant le développement décimal de π[12].
Le problème du collectionneur de vignettes intervient dans l'étude de la complexité en moyenne de l'algorithme de Gale-Shapley[13]. L'objectif de cet algorithme est de calculer un mariage stable. L'algorithme procède comme suit. Chaque homme propose un mariage à la femme qu'il préfère le plus parmi celles à qui il n'a pas encore fait de proposition. Lorsqu'une femme célibataire reçoit une proposition, elle l'accepte. Si elle est mariée, elle accepte une proposition uniquement si cette dernière lui convient mieux. L'analyse en moyenne écrite par Donald Knuth[13] fait une analogie avec le problème du collectionneur de vignettes comme suit. Son analyse repose sur des hommes amnésiques qui font des propositions à des femmes aléatoires. L'algorithme termine alors lorsque les hommes ont fait des propositions à toutes les femmes. L'ensemble des hommes représente les collectionneurs ; les femmes sont les vignettes.

Notes et références

(de) George Pólya, « Eine Wahrscheinlichkeitsaufgabe in der Kundenwerbung », Zeitschrift für Angewandte Mathematik und Mechanik, vol. 10, n^o 1,‎ 1930, p. 96–97 (DOI 10.1002/zamm.19300100113).
L'ouvrage de Feller où il est question du problème est Feller 1968, et la remarque est faite par exemple par Foata, Han et Lass 2001.
Gourdon 2021.
Motwani et Raghavan 1995.
Laplace 1812.
(en) P. Erdös et A. Rényi, « On the Evolution of Random Graphs », Publications of the Mathematical Institute of the Hungarian Academy of Sciences, {{Article}} : paramètre « date » manquant (lire en ligne)
(en) B. Bollobás, « The Evolution of Random Graphs », Transactions of the American Mathematical Society, vol. 286, n^o 1,‎ 1984, p. 257–274 (DOI 10.2307/1999405)
Foata, Han et Lass 2001.
Sardy et Velenik 2010.
Certains exemples de cette partie proviennent de Boneh et Hofri 1997.
Boneh 1983.
Delahaye 2023.
. Donald Knuth, Mariages Stables et leurs relations avec d'autres problèmes combinatoires, Montréal, Les Presses de l'Université de Montréal, 1976, 106 p. (ISBN 978-2-7606-0529-9, présentation en ligne).

Bibliographie

Étude détaillée du problème

Xavier Gourdon, Les maths en tête, t. Algèbre - Probabilités, Paris, Ellipses, 2021, 3^e éd. (1^re éd. 1994), 414 p. (ISBN 978-2-340-05676-3), chap. 6 (« Probabilités »), problème n^o 9 (Problème du collectionneur), p. 356–359 [lire en ligne].
Gilles Pagès et Claude Bouzitat (ill. Yves Guézou, avec le concours de Fabrice Carrance et Frédérique Petit), En passant par hasard : Les probabilités de tous les jours, Paris, Vuibert, 1999, 268 p. (ISBN 2-7117-5258-5), « Pour quelques images de plus ».

Vulgarisation et aspects généraux

Pierre-Simon de Laplace, Théorie analytique des probabilités, Paris, Courcier, 1812, p. 195 [lire en ligne].
Sylvain Sardy et Yvan Velenik, « Petite collection d’informations utiles pour collectionneur compulsif », sur Images des maths, 11 août 2010.
(en) Arnon Boneh et Micha Hofri, « The coupon-collector problem revisited—a survey of engineering problems and computational methods », Stochastic Models (en), Taylor & Francis, vol. 13, n^o 1,‎ 1997, p. 39–66 (DOI 10.1080/15326349708807412, lire en ligne).
(en) William Feller, An Introduction to Probability Theory and Its Applications, vol. 1, New York, Wiley, 1968, 3^e éd., p. 225.
(en) Rajeev Motwani et Prabhakar Raghavan, Randomized Algorithms, Cambridge, New York et Melbourne, Cambridge University Press, 1995 (réimpr. 1997, 2000), 1^re éd., 476 p. (ISBN 978-0-521-47465-8, lire en ligne), chap. 3.6 (« The Coupon Collector's Problem »), p. 57–63.
Robert Ferréol, « Le problème du collectionneur », Tangente Sup,‎ février 2014, p. 52–56 (lire en ligne).
Jean-Paul Delahaye, « Les dures lois des collections », Pour la science, n^o 547,‎ mai 2023, p. 80–85 (lire en ligne).

Articles et ouvrages de recherche

(en) Arnon Boneh, « Preduce—A probabilistic algorithm identifying redundancy by a random feasible point generator (RFPG) », dans Redundancy in Mathematical Programming, Springer, 1983, p. 108–134.
(en) Aimo Torn et Antanas Zilinskas, Global optimization, Springer-Verlag, 1989.
Dominique Foata, Guo-Niu Han et Bodo Lass, « Les nombres hyperharmoniques et la fratrie du collectionneur de vignettes », Séminaire Lotharingien de Combinatoire, vol. 47,‎ 2001 (lire en ligne).

Voir aussi

Source de la traduction

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Coupon collector's problem » (voir la liste des auteurs).

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.