Intégrale de Darboux

Soit ${\displaystyle [a,b]}$ un segment inclus dans ${\displaystyle \mathbb {R} }$. Une subdivision de ce segment est la donnée d'une suite finie de points ${\displaystyle \sigma =(x_{0},\dots ,x_{n})}$ telle que ${\displaystyle a=x_{0}<\cdots <x_{n}=b}$.

Définition (Sommes de Darboux) — Soit une fonction ${\displaystyle f:[a,b]\rightarrow \mathbb {R} }$ bornée et ${\displaystyle \sigma =(x_{0},\dots ,x_{n})}$ une subdivision de ${\displaystyle [a,b]}$. On définit, respectivement, les sommes de Darboux inférieure et supérieure associées à ${\displaystyle f}$ et ${\displaystyle \sigma }$ de la manière suivante :

${\displaystyle S_{-}(f,\sigma ):=\sum _{i=1}^{n}(x_{i}-x_{i-1})\inf _{[x_{i-1},x_{i}]}f\qquad S_{+}(f,\sigma ):=\sum _{i=1}^{n}(x_{i}-x_{i-1})\sup _{[x_{i-1},x_{i}]}f.}$

Sommes de Darboux inférieure (en vert) et supérieure (vert et gris) sur une subdivision en quatre sous-intervalles.

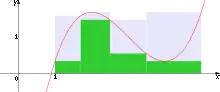
Supposer que la fonction ${\displaystyle f}$ est bornée est indispensable pour définir les sommes de Darboux. En effet, cela permet d'assurer que ${\displaystyle f}$ possède bien un infimum et un supremum finis sur chaque sous-intervalle de la subdivision ${\displaystyle \sigma }$.

Il est clair que, pour une même subdivision, on a toujours que la somme de Darboux inférieure est plus petite que la somme de Darboux supérieure. Puisque ${\displaystyle f}$ est bornée, il existe deux réels ${\displaystyle m}$ et ${\displaystyle M}$ tels que ${\displaystyle m\leqslant f\leqslant M}$. Il est alors clair que pour toute subdivision ${\displaystyle \sigma }$ on a ${\displaystyle m\leqslant S_{-}(f,\sigma )\leqslant S_{+}(f,\sigma )\leqslant M}$.

Soit ${\displaystyle [a,b]}$ un segment inclus dans ${\displaystyle \mathbb {R} }$ et ${\displaystyle \Sigma }$ l'ensemble de ses subdivisions.

Définition (Intégrales de Darboux inférieure et supérieure) — Soit une fonction ${\displaystyle f:[a,b]\rightarrow \mathbb {R} }$ bornée. On définit, respectivement, les intégrales de Darboux inférieure et supérieure associées à ${\displaystyle f}$ de la manière suivante :

${\displaystyle I_{-}(f):=\sup _{\sigma \in \Sigma }S_{-}(f,\sigma )\qquad I_{+}(f):=\inf _{\sigma \in \Sigma }S_{+}(f,\sigma ).}$

Du fait que ${\displaystyle f}$ soit bornée, les intégrales de Darboux sont toujours bien définies et à valeurs réelles. De plus, si ${\displaystyle m\leqslant f\leqslant M}$, alors ${\displaystyle I_{-}(f)\leqslant M}$ et ${\displaystyle m\leqslant I_{+}(f)}$.

Dans certains ouvrages, un symbole intégral souligné ou surligné représentent les intégrales de Darboux inférieure et supérieure :

${\displaystyle I_{-}(f)={\underline {\int _{a}^{b}}}f(x)\,\mathrm {d} x\qquad I_{+}(f)={\overline {\int _{a}^{b}}}f(x)\,\mathrm {d} x}$

Lorsque ${\displaystyle I_{-}(f)=I_{+}(f)}$, cette valeur commune est appelée intégrale de Darboux[3].

Définition (Intégrale de Darboux) — Soit une fonction ${\displaystyle f:[a,b]\rightarrow \mathbb {R} }$ bornée. On dit que ${\displaystyle f}$ est Darboux-intégrable (ou intégrable au sens de Darboux) si les intégrales de Darboux inférieure et supérieure sont égales :

${\displaystyle I_{-}(f)=I_{+}(f)}$.

Dans ce cas, on appelle cette valeur commune l'intégrale (au sens de Darboux) de ${\displaystyle f}$ sur ${\displaystyle [a,b]}$ et on la note

${\displaystyle \int _{a}^{b}f=\int _{a}^{b}f(t)dt}$.

Plutôt que de passer par les sommes de Darboux, il est possible de définir les intégrales inférieure et supérieure de Darboux via des fonctions en escalier, pour lesquelles l'intégrale se définit aisément. En effet, pour une fonction en escalier, l'aire sous la courbe correspond simplement à la somme des aires des rectangles formés par cette dernière.

Plus formellement, une fonction en escalier sur un segment ${\displaystyle [a,b]}$ est une fonction ${\displaystyle g:[a,b]\rightarrow \mathbb {R} }$ telle qu'il existe une subdivision ${\displaystyle \sigma =(x_{0},\dots ,x_{n})}$ de ce segment telle que ${\displaystyle g}$ est constante, sur chaque sous-intervalle ${\displaystyle ]x_{i-1},x_{i}[}$ de la subdivision. Certains ouvrages imposent que ${\displaystyle g}$ soit constante sur les intervalles ${\displaystyle [x_{i-1},x_{i}[}$ ou encore sur les intervalles ${\displaystyle ]x_{i-1},x_{i}]}$. Cela n'aura aucun impact sur la notion d'intégrale puisque cette dernière ne dépendra pas des valeurs prises en un nombre fini de points.

Pour une fonction en escalier ${\displaystyle g:[a,b]\rightarrow \mathbb {R} }$ adaptée à la subdivision ${\displaystyle \sigma =(x_{0},\dots ,x_{n})}$, on définit son intégrale de la manière suivante :

$${\displaystyle \int _{a}^{b}g(t)dt:=\sum _{i=0}^{n}(x_{i-1}-x_{i})c_{i}}$$

où ${\displaystyle c_{i}}$ correspond à la valeur prise par ${\displaystyle g}$ sur ${\displaystyle ]x_{i-1},x_{i}[}$. A noter que cette définition est compatible avec ce qui précède car on peut montrer que l'intégrale de Darboux (telle que définie auparavant) d'une fonction en escalier est bien donnée par la formule ci-dessus.

On constate que les sommes de Darboux peuvent alors s'interpréter comme des intégrales de fonctions en escalier. En effet, soit ${\displaystyle f:[a,b]\rightarrow \mathbb {R} }$ une fonction bornée et ${\displaystyle \sigma =(x_{0},\dots ,x_{n})}$ une subdivision. Si l'on définit deux fonctions en escalier ${\displaystyle g}$ et ${\displaystyle h}$ telles que ${\displaystyle g}$ vaut ${\displaystyle \inf\{f(t):x_{i-1}\leqslant t\leqslant x_{i}\}}$ et ${\displaystyle h}$ vaut ${\displaystyle \sup\{f(t):x_{i-1}\leqslant t\leqslant x_{i}\}}$ sur ${\displaystyle ]x_{i-1},x_{i}[}$ pour tout ${\displaystyle 0\leqslant i\leqslant n}$ (et prennent des valeurs quelconques en les ${\displaystyle x_{i}}$) alors

$${\displaystyle S_{-}(f,\sigma )=\int _{a}^{b}g(t)dt,\qquad S_{+}(f,\sigma )=\int _{a}^{b}h(t)dt.}$$

Ce simple constat permet aisément de réinterpréter les intégrales de Darboux inférieure et supérieure de la manière suivante :

$${\displaystyle I_{-}(f)=\sup \left\{\int _{a}^{b}g(t)dt:g{\text{ en escalier et }}g\leq f\right\},\qquad I_{+}(f)=\inf \left\{\int _{a}^{b}h(t)dt:h{\text{ en escalier et }}h\geq f\right\}.}$$

En passant à un raffinement, la somme inférieure augmente et la somme supérieure décroit.

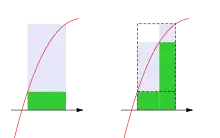
Soit ${\displaystyle f:[a,b]\rightarrow \mathbb {R} }$ une fonction bornée et ${\displaystyle \sigma =(x_{0},\dots ,x_{n})}$ une subdivision de ${\displaystyle [a,b]}$. Si ${\displaystyle \rho =(z_{0},\dots ,z_{m})}$ est un raffinement de ${\displaystyle \sigma }$, c'est-à-dire, si

$${\displaystyle \{x_{0},\dots ,x_{n}\}\subset \{z_{0},\dots ,z_{m}\}}$$

alors on a les inégalités

$${\displaystyle S_{-}(f,\sigma )\leq S_{-}(f,\rho )\quad {\text{et}}\quad S_{+}(f,\rho )\leq S_{+}(f,\sigma )}$$

Autrement dit, en raffinant une subdivision, les sommes de Darboux se rapprochent de la véritable valeur de l'intégrale de ${\displaystyle f}$ (lorsqu'elle est Darboux-intégrable).

Soit ${\displaystyle f:[a,b]\rightarrow \mathbb {R} }$ une fonction bornée. les sommes de Darboux inférieures sont minorées par l'aire du rectangle de largeur ${\displaystyle b-a}$ et de hauteur ${\displaystyle \inf f}$ sur ${\displaystyle [a,b]}$. De même, les sommes de Darboux supérieures sont majorées par l'aire du rectangle de largeur ${\displaystyle b-a}$ et de hauteur ${\displaystyle \sup f}$. Ainsi pour toute subdivision ${\displaystyle \sigma }$ :

$${\displaystyle (b-a)\inf _{[a,b]}f\leq S_{-}(f,\sigma )\leq I_{-}(f)\quad {\text{et}}\quad I_{+}(f)\leq S_{+}(f,\sigma )\leq (b-a)\sup _{[a,b]}f}$$

Si ${\displaystyle \sigma _{1}}$ et ${\displaystyle \sigma _{2}}$ sont deux subdivisions, alors il existe une subdivision ${\displaystyle \rho }$ qui est, à la fois, un raffinement de ${\displaystyle \sigma _{1}}$ et de ${\displaystyle \sigma _{2}}$. Ainsi on a

$${\displaystyle S_{-}(f,\sigma _{1})\leq S_{-}(f,\rho )\leq S_{+}(f,\rho )\leq S_{+}(f,\sigma _{2})}$$

On en déduit alors que

$${\displaystyle I_{-}(f)\leq I_{+}(f)}$$

Les intégrales de Darboux inférieure et supérieure satisfont la relation de Chasles (tout comme l'intégrale de Darboux). Plus précisément, soit ${\displaystyle f:[a,b]\rightarrow \mathbb {R} }$ une fonction bornée et ${\displaystyle c\in [a,b]}$. Alors

$${\displaystyle {\underline {\int _{a}^{b}}}f(x)\,\mathrm {d} x={\underline {\int _{a}^{c}}}f(x)\,\mathrm {d} x+{\underline {\int _{c}^{b}}}f(x)\,\mathrm {d} x\quad {\text{et}}\quad {\overline {\int _{a}^{b}}}f(x)\,\mathrm {d} x={\overline {\int _{a}^{c}}}f(x)\,\mathrm {d} x+{\overline {\int _{c}^{b}}}f(x)\,\mathrm {d} x}$$

Les intégrales de Darboux inférieure et supérieure ne sont pas nécessairement linéaires (contrairement à l'intégrale de Darboux). En revanche elles satisfont certaines inégalités. soit ${\displaystyle f,g:[a,b]\rightarrow \mathbb {R} }$ deux fonctions bornées. Alors

$${\displaystyle {\begin{aligned}{\underline {\int _{a}^{b}}}f(x)\,\mathrm {d} x+{\underline {\int _{a}^{b}}}g(x)\,\mathrm {d} x&\leq {\underline {\int _{a}^{b}}}(f(x)+g(x))\mathrm {d} x\\[6pt]{\overline {\int _{a}^{b}}}f(x)\,\mathrm {d} x+{\overline {\int _{a}^{b}}}g(x)\,\mathrm {d} x&\geq {\overline {\int _{a}^{b}}}(f(x)+g(x))\,\mathrm {d} x\end{aligned}}}$$

De plus, pour tout ${\displaystyle \lambda \geqslant 0}$ :

$${\displaystyle {\underline {\int _{a}^{b}}}\lambda f(x)\,\mathrm {d} x=\lambda {\underline {\int _{a}^{b}}}f(x)\,\mathrm {d} x\quad {\text{et}}\quad {\overline {\int _{a}^{b}}}\lambda f(x)\,\mathrm {d} x=\lambda {\overline {\int _{a}^{b}}}f(x)\,\mathrm {d} x}$$

Et pour tout ${\displaystyle \mu \leqslant 0}$ :

$${\displaystyle {\underline {\int _{a}^{b}}}\mu f(x)\,\mathrm {d} x=\mu {\overline {\int _{a}^{b}}}f(x)\,\mathrm {d} x\quad {\text{et}}\quad {\overline {\int _{a}^{b}}}\mu f(x)\,\mathrm {d} x=\mu {\underline {\int _{a}^{b}}}f(x)\,\mathrm {d} x}$$

Soit ${\displaystyle f:[a,b]\rightarrow \mathbb {R} }$ une fonction bornée. Alors la fonction

$${\displaystyle F:x\in [a,b]\rightarrow {\underline {\int _{a}^{x}}}f(t)\,\mathrm {d} t}$$

est lipschitzienne donc continue. Un résultat identique est vérifié pour F définie à partir de l'intégrale de Darboux supérieure.

Un critère équivalent, parfois utile pour démontrer qu'une fonction est Darboux-intégrable, est donné par le résultat suivant[1] - [4].

Théorème (critère d'intégrabilité, version somme) — Soit une fonction ${\displaystyle f:[a,b]\rightarrow \mathbb {R} }$ bornée. Cette fonction est Darboux-intégrable si et seulement si pour tout ${\displaystyle \varepsilon >0}$, il existe une subdivision ${\displaystyle \sigma }$ de ${\displaystyle [a,b]}$ telle que

${\displaystyle S_{+}(f,\sigma )-S_{-}(f,\sigma )\leq \varepsilon }$.

En termes de fonctions en escalier, cela donne :

Théorème (critère d'intégrabilité, version escalier) — Soit une fonction ${\displaystyle f:[a,b]\rightarrow \mathbb {R} }$ bornée. Cette fonction est Darboux-intégrable si et seulement si pour tout ${\displaystyle \varepsilon >0}$, il existe deux fonctions en escalier ${\displaystyle g}$ et ${\displaystyle h}$ telles que ${\displaystyle g\leqslant f\leqslant h}$ et

${\displaystyle \int _{a}^{b}h(t)dt-\int _{a}^{b}g(t)dt\leq \varepsilon }$.

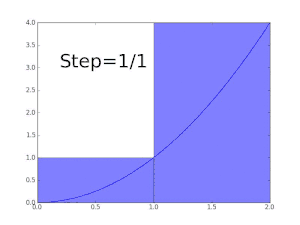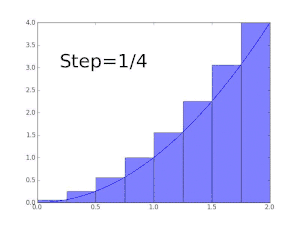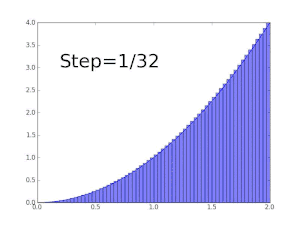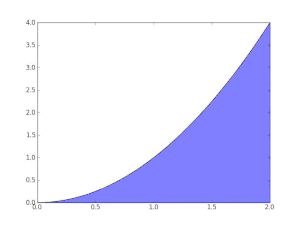
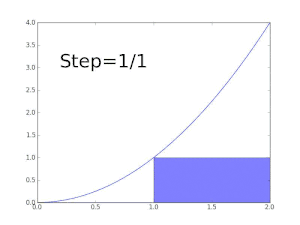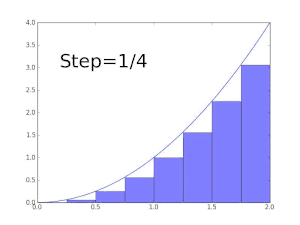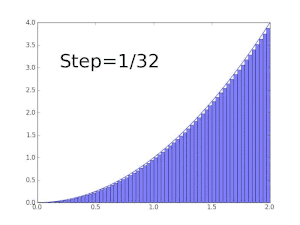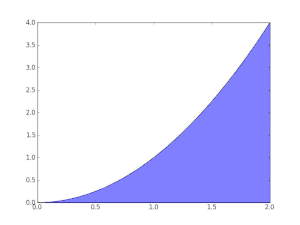
La fonction f(x) = x est Darboux-intégrable sur tout intervalle [a , b].

On considère la subdivision ${\displaystyle \sigma _{n}}$ de [a, b] en n sous-intervalles de même longueur (b – a)/n.

Comme f est strictement croissante, les infimum sur tout sous-intervalle sont atteints en a+(b – a)(k – 1)/n, et les supremum y sont atteints en a+(b – a)k/n. Ainsi

${\displaystyle {\begin{aligned}S_{-}(f,\sigma _{n})&=\sum _{k=1}^{n}f\left(a+(b-a){\frac {k-1}{n}}\right){\frac {b-a}{n}}\\&=\sum _{k=1}^{n}\left(a+(b-a){\frac {k-1}{n}}\right){\frac {b-a}{n}}\\&=n\times a{\frac {b-a}{n}}+{\frac {(b-a)^{2}}{n^{2}}}\sum _{k=1}^{n}(k-1)\\&=a(b-a)+{\frac {(b-a)^{2}}{n^{2}}}\times {\frac {(n-1)n}{2}}\end{aligned}}}$

et

${\displaystyle {\begin{aligned}S_{+}(f,\sigma _{n})&=\sum _{k=1}^{n}f\left(a+(b-a){\frac {k}{n}}\right){\frac {b-a}{n}}\\&=a(b-a)+{\frac {(b-a)^{2}}{n^{2}}}\times {\frac {n(n+1)}{2}}\end{aligned}}}$

On a alors

${\displaystyle S_{+}(f,\sigma _{n})-S_{-}(f,\sigma _{n})={\frac {(b-a)^{2}}{n}}}$

Alors pour tout ε > 0, en choisissant une subdivision ${\displaystyle \sigma _{n}}$ avec ${\displaystyle n>{\frac {(b-a)^{2}}{\epsilon }}}$ on a

${\displaystyle S_{+}(f,\sigma _{n})-S_{-}(f,\sigma _{n})<\epsilon }$

ce qui prouve que f est Darboux-intégrable. La valeur de l'intégrale est alors

${\displaystyle \int _{a}^{b}f(x)\,\mathrm {d} x=\lim _{n\to \infty }S_{-}(f,\sigma _{n})=\lim _{n\to \infty }S_{+}(f,\sigma _{n})={\frac {b^{2}-a^{2}}{2}}}$

Sommes de Darboux

Sommes de Darboux supérieures pour la fonction y = x²

Sommes de Darboux inférieures pour la fonction y = x²

On considère la fonction indicatrice des rationnels sur [0, 1] :

${\displaystyle {\begin{aligned}\chi _{\mathbb {Q} }:[0,1]&\to \mathbb {R} \\x&\mapsto {\begin{cases}1&{\text{si }}x\in \mathbb {Q} \\0&{\text{si }}x\notin \mathbb {Q} \end{cases}}\end{aligned}}}$

Comme les ensembles des nombres rationnels et irrationnels sont tous deux denses dans ℝ, sur tout sous-intervalle de toute subdivision ${\displaystyle \sigma }$, la fonction prend les valeurs 0 et 1 donc

${\displaystyle S_{-}(\chi _{\mathbb {Q} },\sigma )=0\quad {\text{et}}\quad S_{+}(\chi _{\mathbb {Q} },\sigma )=1,}$

si bien que les intégrales de Darboux inférieure et supérieure sont

${\displaystyle I_{-}(\chi _{\mathbb {Q} })=0\quad {\text{et}}\quad I_{+}(\chi _{\mathbb {Q} })=1.}$

Comme elles sont différentes, la fonction n'est pas Darboux-intégrable.

• Intégrale d'une fonction réglée
• Intégrale de Lebesgue
• Rectangle à limite minimum
• Mesure de Jordan

• (en) « Darboux integral », dans Michiel Hazewinkel, Encyclopædia of Mathematics, Springer, 2002 (ISBN 978-1556080104, lire en ligne)
• (en) Michael Spivak, Calculus, Publish or Perish, 2008, 4^e éd. (ISBN 978-0914098911, lire en ligne )