Mesure de Jordan

Un pavé est la généralisation en dimension n d'un parallélépipède rectangle.

Dans l'espace euclidien Rⁿ, un pavé fermé[2] est un produit P = I₁ × … × I_n de n segments I_j = [a_j, b_j]. Son volume est le produit (éventuellement nul) des longueurs b_j – a_j de ces segments. Son intérieur est le pavé ouvert produit des intervalles ouverts bornés ]a_j, b_j[.

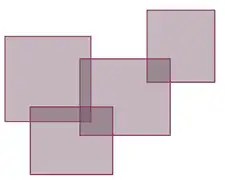
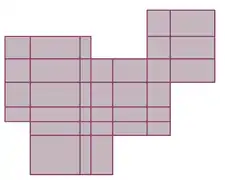
Une partie pavable[3] est une réunion finie X de pavés fermés P_k. On peut alors toujours redécouper X de telle façon que les P_k soient d'intérieurs disjoints, et l'on vérifie qu'ainsi, la somme de leurs volumes ne dépend pas du découpage choisi — d'ailleurs, plus généralement, l'intégrale d'une fonction en escalier sur Rⁿ ne dépend pas de la subdivision adaptée choisie[4]. On note vol(X) cette somme, qu'on appelle le volume (ou la mesure de Jordan) de X.

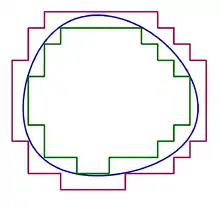
Le paragraphe précédent permet de reformuler géométriquement cette définition : pour toute partie bornée X de Rⁿ, on définit les mesures intérieure et extérieure de Jordan de X, λ^–(X) et λ⁺(X), respectivement, comme la borne supérieure des volumes de parties pavables incluses dans X et la borne inférieure des volumes de parties pavables contenant X, et l'on démontre qu'elles sont égales aux intégrales inférieure et supérieure de l'indicatrice de X[5]. Par conséquent[6], X est cubable si et seulement si λ^–(X) = λ⁺(X), et cette valeur commune est alors égale au volume de X.

Les mesures intérieure et extérieures λ^–(X) et λ⁺(X) sont respectivement égales aux mesures de Lebesgue de l'intérieur et de l'adhérence de X[7].

Pour une partie bornée X, les propriétés suivantes sont équivalentes, et X est dite Jordan-négligeable si elle les vérifie[8] :

• pour tout ε > 0, X est recouvert par une famille finie de pavés dont la somme des volumes est majorée par ε (cette condition est plus contraignante que la définition analogue des parties Lebesgue-négligeables, dans laquelle on autorise une suite infinie de pavés) ;
• X est cubable et de volume nul ;
• λ⁺(X) = 0 ;
• l'adhérence de X est Lebesgue-négligeable.

Pour un fermé borné, les deux notions de négligeabilité sont donc équivalentes.

Une partie bornée dénombrable (et a fortiori : réunion dénombrable d'ensembles Jordan-négligeables) n'est pas nécessairement Jordan-négligeable ni même cubable : par exemple, l'ensemble des rationnels de [0, 1] n'est pas cubable.

Tout convexe borné est cubable[8].

La Jordan-mesurabilité est préservée par union et intersection finies et par différence ensembliste. En particulier, une partie A d'un pavé P est cubable si et seulement si P\A l'est.

Une partie bornée est cubable si et seulement si sa frontière est négligeable (au sens de Lebesgue ou de Jordan, qui sont ici équivalents)[9].

Un fermé borné (ou un ouvert borné) n'est donc pas nécessairement cubable. Par exemple, le compact de Smith-Volterra-Cantor ne l'est pas : sa mesure intérieure est nulle (puisque son complémentaire est dense) alors que sa mesure extérieure est égale à sa mesure de Lebesgue, qui est non nulle.

Pour toute fonction positive bornée f sur une partie cubable A de Rⁿ, l'ensemble des points (x, t) de Rⁿ⁺¹ tels que x ∈ A et 0 ≤ t ≤ f(x) est cubable si et seulement si f est Riemann-intégrable[10].

La mesure de Lebesgue coïncide avec celle de Jordan sur les ensembles cubables, mais elle est définie pour une classe beaucoup plus large d'ensembles, comme les ensembles dénombrables (qui sont Lebesgue-négligeables), et aussi pour des ensembles qui peuvent être non bornés ou pour des fractales. En outre, la mesure de Lebesgue, contrairement à la mesure de Jordan, est une vraie mesure, vérifiant la propriété d'additivité dénombrable.

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Jordan measure » (voir la liste des auteurs).
• (en) Emmanuele DiBenedetto, Real analysis, Basel, Switzerland, Birkhäuser, 2002, 485 p. (ISBN 978-0-8176-4231-0, lire en ligne)
• (en) Richard Courant et Fritz John, Introduction to Calculus and Analysis, vol. II/1, Berlin, Springer, coll. « Classics in Mathematics », 1999, 556 p. (ISBN 978-3-540-66569-4, lire en ligne), chap. 1-4

• Intégrale de Darboux

(en) A. P. Terekhin, « Jordan measure », dans Michiel Hazewinkel, Encyclopædia of Mathematics, Springer, 2002 (ISBN 978-1556080104, lire en ligne)