Homologie (transformation géométrique)
En géométrie projective, une homologie est une transformation projective bijective (dite également homographie), admettant un hyperplan de points fixes et un point fixe extérieur à cet hyperplan, une élation est une transformation projective ayant un hyperplan de points fixes, mais aucun autre point fixe. L'hyperplan est appelé base ou axe de l'homologie comme de l'élation.
.gif)
Dans le cas d'une homologie, le point fixe extérieur est appelé centre ou sommet de l'homologie. Toutes les droites passant par le sommet d'une homologie sont invariantes par celle-ci puisqu'elles passent par deux points fixes. Dans le cas d'une élation on montre qu'il existe un point de l'hyperplan tel que toutes les droites passant par ce point sont globablement invariantes par l'élation, et ce point est appelé centre ou sommet de l'élation.
Parfois toutes les transformations projectives ayant un hyperplan de points fixes sont appelées homologies, c'est-à-dire qu'en plus des homologies telles que définies ci-dessus, les élations deviennent des homologies particulières, dont le sommet est situé sur la base.
Les homologies (au sens restreint) sont les transformations projectives induites par une dilatation, les élations sont celles qui sont induites par une transvection. En dimension finie, de même que les dilatations et les transvections d'un espace vectoriel E engendrent le groupe général linéaire de E, les homologies et les élations d'un espace projectif P(E) engendrent le groupe projectif linéaire de E, qui est le groupe des transformations projectives de P(E).
Définitions
L'espace projectif P(E) peut se définir comme l'ensemble dont les points sont les droites vectorielles de l'espace vectoriel E. Une transformation projective de P(E) qui fixe point par point l'hyperplan projectif H = P(H) est une transformation projective induite par une transformation linéaire f qui conserve chaque droite de H, hyperplan vectoriel de E, c'est-à-dire que tous les vecteurs de H sont vecteurs propres de f. La restriction de f à H est alors une homothétie de rapport non nul, et en divisant si nécessaire f par ce rapport, ce qui induit la même transformation projective, on peut supposer que la restriction de f à H est l'identité.
De telles transformations linéaires de l'espace vectoriel E qui ont un hyperplan de points fixes, soit sont diagonalisables, et appelées dilatations, soit ne sont pas diagonalisables, donc ont 1 pour seule valeur propre, et sont appelées transvections. En dimension finie, il existe une base dans laquelle la matrice de f s'écrit,
si f est une dilatation
si f est une transvection
.
Une transformation projective de P(E) possédant un hyperplan de points fixes est donc[1]
- soit induite par une dilatation vectorielle de E, une telle transformation projective, est appelée homologie,
- soit induite par une transvection vectorielle de E, une telle transformation projective, est appelée élation.
Les élations sont parfois considérées comme des homologies particulières, les homologies de P(E) sont alors toutes les transformations projectives possédant un hyperplan de points fixes[2]. Dans ce contexte les homologies induites par une dilatation peuvent être appelées homologies générales, et les élations homologies spéciales[3].
Homologies
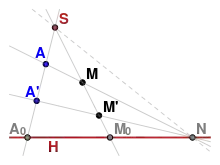
Une homologie induite par une dilatation d'hyperplan H possède un point fixe S hors de H=P(H) qui correspond à une droite de vecteurs propres associé à λ rapport de la dilatation (le sous-espace propre associé dès que λ ≠ 1). Ce point fixe est appelé sommet ou centre de l'homologie, H, hyperplan de points fixes, est appelé base ou axe de l'homologie, on parle aussi d'homologie d'axe H et de centre S. Si l'homologie n'est pas l'identité c'est le seul point fixe hors de H.
En dimension ≥ 2, l'homologie est déterminée par l'axe H, le sommet S, un point A hors de H et distincts de S et son image A' (sur la droite (SA) ). En effet il est alors possible de construire l'image d'un point quelconque de P(E).
- Soit M un point de P(E) distinct de S et hors de H et de la droite (SA). Toutes les droites passant par S sont globalement invariantes car elles intersectent H et passent donc par deux points fixes. Soit N le point d'intersection de la droite (AM) et de H. Ce point étant fixe l'image de la droite (AM) est la droite (A'N). L'image M' de M est donc à l'intersection de la droite (A'N) et de la droite (SM), toutes deux coplanaires, ce qui détermine M'.
- Si M est sur la droite (SA) on obtient son image en passant par un point extérieur et en appliquant 2 fois la construction précédente.
Soit A0 l'intersection de la droite (SA) et de l'hyperplan H, M0 l'intersection de la droite (SM) et de H. Le birapport [S, A0, A, A'] = [S, M0, M, M' ] ne dépend pas du choix du point M. Il est appelé rapport ou birapport de l'homologie. En dimension ≥ 2, une homologie est déterminée par son axe, son centre et son birapport[1].
En particulier, dans une homologie de birapport égal à -1, les points S, M0, M, M' sont en division harmonique. Une telle homologie porte le nom d'homologie harmonique, c'est une homologie involutive. Ce sont les seules homologies involutives[1].
Élations
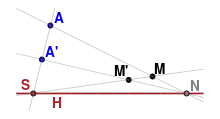
Soit v un vecteur non nul de la direction de la transvection f, on a pour une certaine forme linéaire a et x ∈ E
- f(x) = x + a(x)v
On appelle sommet ou centre de l'élation induite par f le point de P(E) correspondant à la direction de la transvection f, soit la droite de vecteur directeur v. Les vecteurs x, v et f(x) sont coplanaires, ce qui se traduit projectivement par le fait que le sommet de l'élation, un point et son image sont alignés, c'est-à-dire que les droites passant par le sommet de l'élation sont globablement invariantes[4].
Une élation est déterminée par sa base H, un point A hors de H, et son image A'. La construction de l'image M' d'un point M est analogue à celle effectuée dans le cas de l'homologie[4].
Caractérisation par le centre
Les droites passant par le centre d'une homologie ou par le centre d'une élation sont globalement invariantes par celle-ci. Cette propriété est caractéristique :
- une homographie est une homologie ou une élation si et seulement si elle possède un point fixe tel que les droites passant par ce point sont globalement invariantes[5].
En géométrie affine
Soit h une homologie ou élation de l'espace projectif P(E). La structure projective induit sur le complémentaire d'un hyperplan de P(E) une structure d'espace affine, l'hyperplan étant dit hyperplan à l'infini de cet espace affine. Si cet hyperplan est stable par h, la restriction de h au complémentaire est une application affine. Les seuls hyperplans stables par une homologie ou une élation distincte de l'identités sont l'hyperplan de base et les hyperplans passant par le sommet[6].
Dans le cas d'une homologie, le birapport tel que défini ci-dessus est un quotient de deux rapports de mesures algébriques, soit
L'hyperplan de base comme hyperplan à l'infini
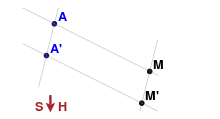
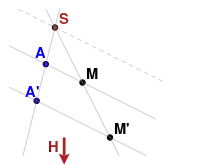
L'hyperplan projectif H qui est la base de l'homologie ou élation h est évidemment stable par h. Le complémentaire E1 de H est muni d'une structure d'espace affine telle que les droites parallèles dans E1 sont les droites de P(E) sécantes en un point de H. La restriction de h à E1 est alors une application affine qui transforme une droite en une droite parallèle, et donc :
- la restriction d'une homologie ou élation à l'espace affine complémentaire de son hyperplan de base est une homothétie ou une translation.
De façon plus précise
- la restriction au complémentaire de son hyperplan de base d'une homologie de centre S de rapport λ est une homothétie de centre S et de rapport inverse 1/λ.
- la restriction au complémentaire de son hyperplan de base d'une élation est une translation (le sommet de l'élation est à l'infini).
Les homologies de rapport -1 dites harmoniques, ont pour restriction une symétrie centrale.
Le sommet est à l'infini
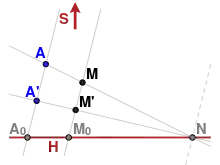
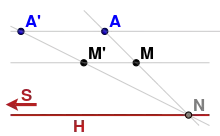
Un hyperplan H∞ passant par le sommet S d'une homologie h d'hyperplan H est stable par h, du fait qu'il est engendré par S et son intersection avec H. De même un hyperplan H∞ passant par le sommet d'une élation h d'hyperplan H, cet hyperplan H∞ étant distinct de H, est stable par h, étant engendré par une droite de l'hyperplan passant par S et son intersection avec H.
Dans les deux cas la restriction à l'espace affine complémentaire de H∞ est donc une transformation affine.
- la restriction au complémentaire d'un hyperplan H∞ passant par S d'une homologie de centre S, d'axe H et de rapport λ est une dilatation d'axe H et de rapport inverse λ.
- la restriction au complémentaire d'un hyperplan H∞ passant par S d'une élation de centre S et d'axe H est une transvection d'axe H.
Exemple où l'application n'est pas affine
Dans les autres cas l'application obtenue par restriction ne conserve pas le parallélisme et n'est pas affine. Par exemple si le plan K2 est vu comme hyperplan affine d'équation Z= 1 dans K3, l'homologie (x, y)↦(x', y') d'axe l'axe des abscisses, de centre (0,a) (a ≠ 0), et de rapport λ, est donc induite par la dilatation vectorielle de plan de base ( (1,0,1), (0,0,1) ), un vecteur propre pour la valeur propre λ étant (0,a,1). Dans la base canonique la matrice est donc
c'est une matrice homogène de l'application et celle-ci s'exprime par les formules en coordonnées homogènes :
Par restriction au plan affine K2 l'application est donc définie pour a + (λ -1) y ≠ 0 par
Homologie par perspective
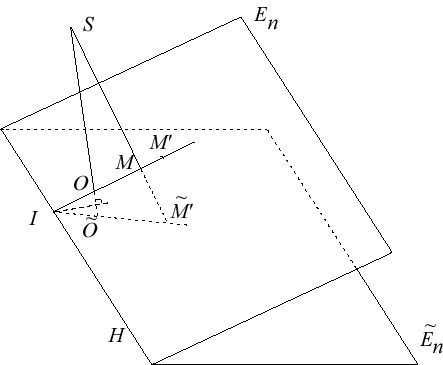 |
Plongeons l'espace euclidien de dimension n comme hyperplan d'un espace de dimension n+1 et faisons tourner autour de son hyperplan , de façon à en obtenir une copie .
Tout point de a une copie dans , donc aussi l'image de par une homologie projective de base et de centre du complété projectif de . On montre que les droites joignant à passent par un point fixe , de sorte que l'application est la restriction d'une projection centrale de centre S. On remarque que se trouve sur la droite passant par et orthogonale à l'hyperplan bissecteur de et . |
Figures homologiques
Deux figures sont dites homologiques si elles sont images l'une de l'autre par une homologie. Ceci constitue une généralisation de la notion de figures homothétiques.
Par exemple deux triangles et sont homologiques si, à permutation près, il existe une homologie envoyant en , en , en ; cela équivaut à ce que les droites et soient concourantes (au centre de l'homologie) ; et cela équivaut aussi à ce que les points d'intersection des droites et , et , et appartiennent à un même hyperplan (la base de l'homologie). L'équivalence entre ces deux dernières propriétés constitue le théorème de Desargues.
Homologie biaxiale
Les homologies biaxiales sont les homographies en dimension 3 ayant deux droites non coplanaires formées de points fixes. Ce ne sont donc pas des homologies au sens général donné ici.
La construction de l'image d'un point se fait simplement grâce à la propriété suivante : Si et sont les uniques points respectifs de et tels que sont alignés, le birapport est constant égal à ; la matrice homogène dans un repère projectif dont les deux premiers points sont sur et les deux suivants sont sur est : .
Les homologies biaxiales peuvent être vues aussi comme les complétées projectives des affinités de base une droite.
Références
- Par exemple Ladegaillerie 2003, p. 142.
- Par exemple Fresnel 1996, p. 72.
- Sidler 2000, p. 38-40.
- Ladegaillerie 2003, p. 143.
- Ladegaillerie 2003, p. 144.
- Ladegaillerie 2003, p. 142-143.
Bibliographie
- Jean Fresnel, Méthodes modernes en géométrie, Paris, Hermann, , 408 p. (ISBN 2-7056-1437-0).
- Yves Ladegaillerie, Géométrie : affine, projective, euclidienne et anallagmatique, Paris, Ellipses, , 515 p. (ISBN 2-7298-1416-7).
- Jacqueline Lelong-Ferrand, Fondements de la géométrie, Paris, PUF, , 287 p. (ISBN 2-13-038851-5).
- Jean-Claude Sidler, Géométrie projective : cours, exercices et problèmes corrigés, Paris, Dunod, , 2e éd. (1re éd. 1993), 206 p. (ISBN 2-10-005234-9)


![[S,A,A_{0},A,A']={\frac {\overline {AS}}{\overline {AA_{0}}}}:{\frac {\overline {A'S}}{\overline {A'A_{0}}}}.](https://img.franco.wiki/i/2239fd29c9db4f58c8369f78c9088790388dbc3b.svg)







































