Gradient thermique adiabatique
Le gradient thermique adiabatique est, dans l'atmosphère terrestre, la variation de température de l'air avec l'altitude, autrement dit le gradient de la température de l'air, qui ne dépend que de la pression atmosphérique, c'est-à-dire[1] :
- sans considération d'échange de chaleur avec l'environnement (autres masses d'air, relief) ;
- sans considération de condensation (formation de nuages) ni de précipitations.

Ce concept a une grande importance en météorologie, ainsi qu'en navigation aérienne et maritime.
Mécanisme
La variation de pression de l'atmosphère terrestre est très complexe. Toutefois, pour comprendre certains mécanismes météorologiques, on peut s'en tenir à un modèle très simple qui ne dépend que de l'altitude. Dans la troposphère, l'air peut être assimilé à un gaz parfait : la pression est relativement faible (de l'ordre de 105 pascals) et les molécules n'ont pas d'interaction autre que des chocs entre elles. Ainsi, si une masse d'air n'échange pas de chaleur avec son environnement (conditions dites adiabatiques), sa température ne dépend que de sa pression : lorsque l'air se comprime, il s'échauffe, et lorsqu'il se détend, il se refroidit.
Dans une atmosphère totalement sèche, on a[1] :
avec :
- la capacité thermique isobare (à pression constante) molaire de l'air (en J/mol·K) ;
- la variation élémentaire de température pour une variation d'altitude ;
- la variation d'altitude ;
- la masse molaire de l'air (en kg/mol) ;
- l'accélération de la gravité (en m/s2).
Ce résultat s'obtient en posant que l'enthalpie généralisée est constante. Si une masse d'air s'élève, elle se refroidit par détente adiabatique (puisque la pression de l'air diminue). Si elle descend, elle se réchauffe par compression adiabatique (puisque la pression de l'air augmente). Cette variation de température avec l'altitude permet de définir le gradient thermique adiabatique.
Gradient adiabatique sec

Dans la troposphère, la température d'une parcelle s'élevant selon le gradient thermique adiabatique est[1] :
avec :
- la température à l'altitude étudiée ;
- la température au niveau de référence ;
- la pression à l'altitude étudiée ;
- la pression au niveau de référence ;
- la constante universelle des gaz parfaits massique () ;
- : capacité thermique isobare (à pression constante) massique de l'air.
Il vaut −9,75 °C par kilomètre ( avec = 9,806 65 m/s2 et = 1006 J/(K·kg)). On utilise souvent la valeur approchée de −10 °C par kilomètre, soit −1 °C pour 100 m[2] ou 3 °C pour mille pieds. La démonstration de la formule ci-dessus est effectuée dans la boîte déroulante de l'article décrivant la variation de la pression atmosphérique avec l'altitude.
Ce gradient est dit gradient adiabatique sec car l'humidité ne joue aucun rôle. Il apparaît sur le diagramme thermodynamique qu'on appelle émagramme ci-joint (lignes pleines nommées Adiabatique sèche), où on voit que la pente est la même quelle que soit la température (les courbes sont parallèles).
Gradient adiabatique humide ou l'influence de l'humidité

En soi, la présence de vapeur d'eau n'a pas d'influence sur le gradient adiabatique. Toutefois, en dessous d'une certaine température, la vapeur d'eau se condense. Cette température dépend de la teneur en vapeur d'eau et de la présence de poussières permettant aux gouttelettes de se former (sorte de floculation). En effet, hors présence de poussière, a lieu la sur-vaporisation : l'eau reste sous forme de vapeur car les gouttelettes qui se forment ne sont pas stables (voir l'article « Surfusion »).
Si la vapeur d'eau se condense, cette liquéfaction libère de la chaleur (chaleur latente de vaporisation) : le Soleil a chauffé l'eau de l'océan et du sol, et cette chaleur a été emmagasinée dans l'évaporation ; le changement d'état inverse redonne cette chaleur. Ainsi, si la vapeur d'eau se condense, la masse d'air se réchauffe.
De fait, la condensation réchauffant l'air, la valeur absolue du gradient est plus faible. Ce taux dépend du relâchement de chaleur latente qui lui dépend légèrement de la pression mais plus fortement de la température ambiante. Le taux adiabatique humide n'est donc pas une constante et varie selon les courbes « adiabatique humide » que l'on voit sur l'image de l'émagramme. Ces courbes changent de pente avec la température et la pression, se rapprochant de l'adiabatique sèche à mesure que l'humidité de l'air est faible (température très froide et/ou faible pression).
Par exemple, le taux moyen est souvent mentionné comme −6 °C/km mais en fait varie ainsi :
- à 1 000 hPa de pression : de −3,15 °C/km (40 °C) à −9,78 °C/km (−40 °C) ;
- à 500 hPa de pression : de −2,55 °C/km (40 °C) à −9,54 °C/km (−40 °C).
La courbe sur tout diagramme thermodynamique qui représente ce gradient pour une parcelle d'air à une température et pression de départ est celle de sa température potentielle constante du thermomètre mouillé. Elle porte différents noms : « gradient adiabatique saturé », « pseudo-adiabatique saturé » (« pseudo » car on élimine l'eau à mesure qu'elle se condense), « adiabatique de saturation » ou « adiabatique humide » [3] - [4].
Franchissement d'un obstacle
Supposons un vent sec parallèle au sol qui rencontre un obstacle du relief (colline, montagne). L'air suit le relief et s'élève, il subit donc une détente qui le refroidit. Puis, lorsque l'air redescend sur l'autre versant, il se réchauffe. Si l'opération a été suffisamment rapide, l'air n'a pas échangé de chaleur avec l'obstacle ni avec l'air d'altitude, il se retrouve donc à la même température de l'autre côté.
Maintenant, si l'humidité de l'air est assez importante, l'eau va se condenser en montant. Deux scénarios peuvent se produire :
- s'il ne pleut pas sur le côté face au vent, en redescendant, l'air se réchauffe et donc les gouttelettes d'eau s'évaporent à nouveau. La chaleur libérée par la liquéfaction en montant est réabsorbée par l'évaporation en descendant, l'air a donc également la même température de l'autre côté du versant ;
- s'il pleut au sommet de la montagne, cela change les conditions, l'air a perdu une partie de son humidité au sommet de la montagne. Il y a donc moins d'eau qui s'évapore et ainsi moins de chaleur absorbée : à altitude égale, l'air de l'autre côté du versant est donc plus chaud.
Atmosphère stable et atmosphère instable
Considérons une masse d'air située au niveau du sol. Pour imaginer cette masse, on peut par exemple considérer un ballon peu gonflé : la pression à l'intérieur du ballon est tout le temps égale à la pression extérieure (la paroi est détendue et n'exerce pas de pression), et la chaleur peut traverser aisément sa paroi. On peut déplacer cette parcelle d'air dans la verticale et sa température changera selon la détente ou compression adiabatique. Voici trois scénarios possibles pour son déplacement ultérieur.
Atmosphère instable
Si le gradient thermique que suit la parcelle est plus grand que le gradient adiabatique, on est en « atmosphère instable ». Si cette masse d'air s'élève en altitude, par exemple sous l'effet du vent, elle rencontre de l'air qui est plus froid qu'elle-même. Donc cette masse d'air est plus chaude que l'air ambiant et donc moins dense. Elle continuera ainsi de monter grâce à la poussée d'Archimède. Inversement, dans les mêmes conditions, si on prend une masse d'air en altitude et qu'on la fait descendre, elle se réchauffe par compression adiabatique, mais moins vite que l'air ambiant qu'elle traverse : elle sera plus froide que l'air des couches inférieures, donc plus dense et elle va continuer à descendre. Les couches instables d'air en mouvement vertical (montée ou descente) voient donc leur mouvement amplifié.
On dit que l'atmosphère est absolument instable lorsque (on parle aussi de gradient thermique superadiabatique). En général, l'atmosphère n'est absolument instable que près du sol surchauffé lors d'une insolation intense. Cette couche est peu épaisse et au-dessus de celle-ci le gradient thermique est celui de l'adiabatique sèche à la suite d'un phénomène de mélange[5] - [6]. L'atmosphère peut aussi être rendue absolument instable en présence d'un vent descendant le long d'une pente chauffée par le soleil (en général par vent du nord sur un versant exposé au midi). En effet, en plus du réchauffement mécanique de la parcelle d'air dû à la compression, l'air va absorber un supplément de chaleur en léchant la pente.
On en conclut donc que le concept d'atmosphère absolument instable loin du sol est en général une vue de l'esprit. Cependant, à l'intérieur d'un nuage convectif, la température d'une parcelle d'air peut devenir supérieure à la température de l'air environnant (définie par l'indice de soulèvement) sans que le gradient de température soit superadiabatique.
Atmosphère stable
Si le gradient thermique de la parcelle est plus petit que le gradient adiabatique, on est en « atmosphère dynamiquement stable » ou en « stabilité hydrostatique »[7]. Dans ce cas, l'air en altitude est plus chaud que l'air montant, donc la masse d'air montante est plus froide que l'air ambiant. La montée s'arrête, car la poussée d'Archimède est plus faible que le poids, et la masse d'air retourne vers son point de départ. Inversement, si la masse d'air descend, elle devient plus chaude que l'air ambiant, la descente s'arrête et la parcelle d'air retourne à son point de départ. Les couches stables d'air ont donc tendance à rester à leur altitude. Il y a deux types d'air stable selon le gradient de température vertical de température de la colonne d'air dans l'atmosphère :
- stabilité absolue[8] : lorsque la température de l'environnement est toujours moindre que celle de l'adiabatique saturé ;
- stabilité conditionnelle : lorsque la température de l'environnement peut être plus rapide que ce gradient au-dessus d'une certaine altitude. Un soulèvement mécanique permet alors d'atteindre une couche instable et le niveau de convection libre.
Ainsi, une couche où le gradient thermique est nul ou négatif, appelées respectivement couche isotherme et couche d'inversion, favorise une stabilité générale de l'air, limitant les développements verticaux de grande ampleur. Elles forment donc un couvercle où les nuages convectifs ne peuvent se former ou ne peuvent dépasser s'ils se forment à une altitude inférieure.
Atmosphère neutre
Une particule qui subit un déplacement vertical et qui ne devient ni plus chaude, ni plus froide que le milieu ambiant, est dite dans une « atmosphère neutre ». Elle demeurera au nouveau niveau car aucune force ne s'exerce sur elle pour continuer à la déplacer ou à revenir à son point de départ.
Gradient sec ou humide

Le gradient adiabatique de la couche évoqué plus haut n'est pas précisé comme étant sec ou humide. Comme une parcelle d'air soulevée ne peut changer de température que selon ces deux courbes :
- une parcelle d'air soulevée ne peut changer de température plus vite que le gradient adiabatique sec. Donc toute couche d'air qui aura un gradient plus grand que celui-ci est par définition instable ;
- une parcelle d'air saturée ne peut, quant à elle, changer de température plus vite que le pseudo-gradient adiabatique humide. Si la couche a un changement de température moindre que ce gradient, on a affaire à une couche stable car elle sera toujours plus chaude que la parcelle soulevée ;
- lorsque le gradient thermique se situe entre le gradient adiabatique sec et le gradient adiabatique saturé, on a une atmosphère potentiellement instable :
- si la parcelle soulevée est saturée et suit l'adiabatique humide, on a une situation instable,
- si la parcelle n'est pas saturée et suit l'adiabatique sèche, on a une situation stable jusqu'à ce que l'on atteigne la saturation par refroidissement d'altitude.
Pour repérer l'instabilité de la masse d'air, on peut pointer la courbe de températures sur un diagramme thermodynamique comme le téphigramme. Sur ces derniers, les taux adiabatiques secs et humides sont tracés et on peut donc facilement les comparer à la courbe.
Instabilité latente
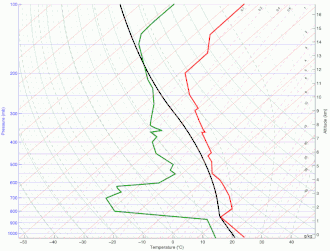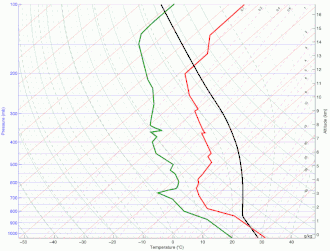
Lorsque le déplacement vertical de l'air est relativement important, une particule peut devenir instable même si au départ elle était stable par rapport à son environnement. Dans l'atmosphère, une forte poussée peut occasionner un déplacement et amener la parcelle jusqu'au niveau de condensation par ascendance où la vapeur d'eau contenu qu'elle contient se mettra à former du nuage. Entrainée plus haut le long de l'adiabatique mouillé, elle peut à partir d'un certain niveau être plus chaude que le milieu ambiant et donc instable. On appelle le niveau où la température de la particule devient tout juste plus élevée que celle de l'environnement; le niveau de convection libre.
On dit qu'une couche où des particules peuvent devenir instables sous l'influence d'un déplacement forcé se caractérise par de l'instabilité latente (IL). Le terme « latent » indique que l'instabilité est cachée mais qu'elle est néanmoins présente sans que cela paraisse de l'extérieur. Celle-ci peut être libérée par :
- un mécanisme d'ascendance suffisamment puissant pour amener les particules d'air jusqu'au niveau de convection libre ;
- une humidité suffisante pour que le niveau de condensation soit atteint le plus rapidement possible. Ainsi le refroidissement causé par l'expansion se retrouvera réduit à la suite du relâchement de chaleur latente provoqué par la condensation.
Il est possible de déterminer quelles sont les couches d'instabilité latente et d'identifier le type d'instabilité latente de façon graphique sur le diagramme thermodynamique.
Instabilité potentielle
Au lieu de considérer juste une parcelle soulevée, on peut regarder ce qui se passe quand toute une couche d'atmosphère est déplacée. L'instabilité engendrée par le soulèvement généralisé d'une couche ou de toute une masse d'air fait référence à l'instabilité potentielle (IP) de la couche. Ce phénomène d'ascendance à grande échelle peut être considéré comme une perturbation significative de l'état de base. Ce soulèvement peut provenir de phénomènes à l'échelle synoptique engendrés par des dépressions, des fronts ou des creux barométriques.
On s'intéressera donc à la stabilité d'une couche qui subit un fort déplacement vertical. Le haut de cette couche se trouve à une température et une pression différente de la base. Le contenu en vapeur d'eau peut varier également dans l'épaisseur de la couche. Deux cas sont possibles.
Dans le premier cas, la couche demeure non saturée et le mouvement vertical s'effectue selon les adiabatiques sèches dans toute la couche. Dans le cas d'un soulèvement uniforme, la couche s'étire sur le plan vertical, tout en se contractant horizontalement car la variation de pression est inversement proportionnelle à la pression. Une partie du gradient vertical de la couche peut alors s'accentuer durant l'ascendance, sa stabilité diminuer et se rapprocher de l'adiabatique sèche. Dans les cas de subsidence et d'étalement horizontal, le gradient vertical devient plus stable. La stabilité ne peut être notablement affectée dans ces deux cas que si les déplacements verticaux ou le cisaillement vertical des mouvements verticaux sont très accentués. Ces phénomènes risquent peu de se produire dans la nature.
Dans le second cas, une partie de la couche sature pendant qu'elle monte. L'air non saturé se refroidit en fonction du gradient adiabatique sec alors que l'air saturé se refroidit en fonction du gradient adiabatique saturé (refroidissement moins prononcé). Ceci donne deux cas possibles :
- si la couche est saturée à la base et sèche au sommet, le gradient vertical augmente car la base se refroidit plus lentement que le sommet de la couche. La couche devient donc plus instable ;
- si à l'inverse, le sommet de la couche est plus humide que la base, le mouvement ascendant stabilisera la couche.
Si la couche descend, l'effet est inversé.
Conséquences
L'atmosphère peut varier de stabilité avec l'altitude. Ainsi on peut retrouver une alternance de couches stables et instables qui donneront des types différents de nuages et des conditions de visibilité et de vent différentes.
Dans une couche instable, on a des mouvements verticaux importants qui donnent :
- des nuages de type cumulus (cumulus, stratocumulus, altocumulus, cirrocumulus et cumulonimbus selon l'altitude) ;
- des vents qui soufflent en rafales par mélange de l'air dans la couche ce qui donne de la turbulence ;
- une bonne visibilité car les particules sont projetées en altitude.
Ceci peut se produit à n'importe quel niveau de la troposphère si on réchauffe la base de la couche et/ou refroidit l'air au sommet.
Dans une couche stable, on a seulement des mouvements verticaux mécaniquement induits (ex. soulèvement par une montagne ou par un front chaud) ce qui donne :
- des nuages de type stratus (brouillard, stratus, altostratus, cirrostratus, cirrus et nimbostratus) ;
- des vents réguliers qui sont étagés laminairement selon l'altitude ;
- une visibilité souvent médiocre par accumulation de particules dans la couche.
Ceci se produit lorsqu'un phénomène refroidit la base de la couche et/ou réchauffe l'air à son sommet.
Dans une couche neutre :
- dans une couche saturée, le gradient vertical du milieu est exactement égal au gradient vertical de l'adiabatique mouillé : les nuages présents restent les mêmes ;
- dans une couche non saturée, le gradient vertical du milieu est exactement égal au gradient vertical de l'adiabatique sec : aucune formation de nuages.
Annexe : Calcul simplifié
Tout gaz parfait diatomique (l'air est considéré comme tel, les autres gaz le composant étant en quantité négligeable) en évolution adiabatique et quasi statique, obéit à la loi :
avec :
- la température absolue (en kelvin) pour une pression ;
- est la température au sol, où la pression est .
Le gradient de température est donc relié au gradient de pression par la relation :
Le tableau de variation de pression avec l'altitude permet donc de déterminer ce gradient thermique :
- on prend = 1 013 hPa et = 288,15 K (15 °C0) ;
- on considère la différence de pression entre deux altitudes du tableau, ce qui donne la différence de température absolue relative entre deux altitudes ;
- est alors calculée à partir de la température à l'altitude précédente et du gradient relatif.
Le tableau suivant considère une masse d'air partant du sol et s'élevant.
| altitude (km) | pression (hPa) | température (K) | température (°C) | (hPa) | (sans unité) | (sans unité) | (K) |
|---|---|---|---|---|---|---|---|
| 0 | 1013 | 288,15 | 15 | ||||
| 0,5 | 955 | 283,44 | 10,29 | −58 | −0,057 | −0,016 | −4,71 |
| 1 | 900 | 278,77 | 5,62 | −55 | −0,058 | −0,016 | −4,66 |
| 1,5 | 845 | 273,90 | 0,75 | −55 | −0,061 | −0,017 | −4,87 |
| 2 | 794 | 269,18 | - 3,97 | −51 | −0,060 | −0,017 | −4,72 |
| 2,5 | 746 | 264,53 | - 8,62 | −48 | −0,060 | −0,017 | −4,65 |
| 3 | 700 | 259,87 | - 13,28 | −46 | −0,062 | −0,018 | −4,66 |
| 3,5 | 658 | 255,42 | - 17,73 | −42 | −0,06 | −0,017 | −4,45 |
| 4 | 617 | 250,87 | - 22,8 | −41 | −0,062 | −0,018 | −4,55 |
| 5 | 541 | 242,04 | - 33,11 | −76 | −0,123 | −0,035 | −8,83 |
| 6 | 471 | 233,09 | - 42,06 | −70 | −0,129 | −0,037 | −8,95 |
| 7 | 411 | 224,61 | - 50,54 | −60 | −0,127 | −0,036 | −8,48 |
| 8 | 357 | 216,18 | - 56,97 | −54 | −0,131 | −0,038 | −8,43 |
| 9 | 331 | 211,68 | - 63,47 | −26 | −0,073 | −0,021 | −4,50 |
| 10 | 265 | 199,62 | - 75,53 | −66 | −0,199 | −0,057 | −12,06 |
| 11 | 227 | 191,44 | - 83,71 | −38 | −0,143 | −0,041 | −8,18 |
| 12 | 194 | 183,49 | - 91,66 | −33 | −0,145 | −0,042 | −7,95 |
La température ainsi calculée est très différente de la température de l'air réelle que l'on s'attend à rencontrer.
Si l'on refait le calcul en considérant que la masse d'air part de l'altitude (donc à la température ) pour aller à l'altitude on obtient le tableau suivant.
| altitude (km) | pression (hPa) | température (K) | (hPa) | (sans unité) | (sans unité) | (K) |
|---|---|---|---|---|---|---|
| 0 | 1013 | 288,15 | ||||
| 0,5 | 955 | 282,15 | −58 | −0,057 | −0,016 | −4,71 |
| 1 | 900 | 280,15 | −55 | −0,058 | −0,016 | −4,64 |
| 1,5 | 845 | 278,15 | −55 | −0,061 | −0,017 | −4,89 |
| 2 | 794 | 275,15 | −51 | −0,060 | −0,017 | −4,80 |
| 2,5 | 746 | 272,15 | −48 | −0,060 | −0,017 | −4,75 |
| 3 | 700 | 270,15 | −46 | −0,062 | −0,018 | −4,79 |
| 3,5 | 658 | 267,15 | −42 | −0,06 | −0,017 | −4,63 |
| 4 | 617 | 263,15 | −41 | −0,062 | −0,018 | −4,76 |
| 5 | 541 | 257,15 | −76 | −0,123 | −0,035 | −9,26 |
| 6 | 471 | 250,15 | −70 | −0,129 | −0,037 | −9,51 |
| 7 | 411 | 242,15 | −60 | −0,127 | −0,036 | −9,10 |
| 8 | 357 | 235,15 | −54 | −0,131 | −0,038 | −9,09 |
| 9 | 331 | 232,15 | −26 | −0,073 | −0,021 | −4,89 |
| 10 | 265 | 222,15 | −66 | −0,199 | −0,057 | −13,23 |
| 11 | 227 | 218,15 | −38 | −0,143 | −0,041 | −9,10 |
| 12 | 194 | 217,15 | −33 | −0,145 | −0,041 | −9,06 |
Le gradient thermique est défini comme le rapport entre la variation de température divisé par la variation d'altitude , exprimé en kelvin par kilomètre (K/km), ou, ce qui est équivalent, en degré Celsius par kilomètre (°C/km). Le tableau ci-dessous synthétise le gradient thermique adiabatique pour les deux modèles.
| Altitude (km) |
Gradient thermique adiabatique (°C/km) |
Gradient thermique du modèle OACI (°C/km) |
Température (°C) | ||
|---|---|---|---|---|---|
| modèle 1 | modèle 2 | modèle 1 | modèle 2 | ||
| 0,5 | −9,43 | −9,43 | −6,5 | 10 | 9 |
| 1 | −9,33 | −9,29 | 9 | 7 | |
| 1,5 | −9,73 | −9,78 | 1 | 5 | |
| 2 | −9,45 | −9,59 | −4 | 2 | |
| 2,5 | −9,30 | −9,51 | −9 | −1 | |
| 3 | −9,32 | −9,59 | −13 | −3 | |
| 3,5 | −8,91 | −9,26 | −18 | −6 | |
| 4 | −9,09 | −9,51 | −22 | −10 | |
| 5 | −8,83 | −9,26 | −31 | −16 | |
| 6 | −8,95 | −9,51 | −40 | −23 | |
| 7 | −8,48 | −9,10 | −49 | −31 | |
| 8 | −8,43 | −9,09 | −57 | −38 | |
| 9 | −4,50 | −4,89 | −61 | −41 | |
| 10 | −12,06 | −13,23 | −74 | −51 | |
| 11 | −8,18 | −9,10 | −82 | −55 | |
| 12 | −7,95 | −9,06 | −90 | −56 | |
On constate que les gradients thermiques adiabatiques calculés par le modèle 1 et par le modèle 2 sont assez peu différents, mais que ces valeurs sont très différentes du gradient réel ; le gradient thermique imposé par les températures du sol et de l'espace est donc très différent du gradient thermique adiabatique.
On remarque également que dans le modèle OACI, si une masse d'air s'élève du sol (modèle 1), elle se refroidit plus vite que l'air ambiant (modèle 2, OACI) ; cette masse d'air ascendante va donc échanger de la chaleur avec l'air ambiant et se refroidir, et donc redescendre. Le modèle OACI est donc un modèle d'atmosphère stable.
Notes et références
- « Le Gradient adiabatique », Comprendre la météo, sur Météo-France (consulté le ).
- (en) Paul Markowski et Yvette Richardson, Mesoscale Meteorology in Mid latitudes, Chichester, Wiley-Blackwell, , 407 p. (ISBN 978-0-470-74213-6), p. 16.
- Organisation météorologique mondiale, « Adiabatique de saturation », Eumetcal (consulté le ).
- G.-Oscar Villeneuve, Glossaire de météorologie et de climatologie, Laval, Les Presses de l'Université Laval, , 645 p. (ISBN 2-7637-6896-2, lire en ligne), p. 4.
- (en) Thomas Tomkins Warner, Numerical Weather and Climate Prediction, Cambridge, Cambridge University Press, , 526 p. (ISBN 978-0-521-51389-0), p. 91.
- (en) anonyme, Glider Flying Handbook, Federal Aviation Administration (lire en ligne [PDF]), p. 9-8.
- Organisation météorologique mondiale, « Stabilité hydrostatique », sur Eumetcal (consulté le ).
- Organisation météorologique mondiale, « Stabilité absolue », sur Eumetcal (consulté le ).
Bibliographie
- (en) R.G. Barry et R.J. Chorley, Atmosphere, weather and climate, 7e édition, Routledge, 1998, p. 80-81 (ISBN 0-415-16020-0).
- (en) M. K. Yau et R. R. Rogers, Short Course in Cloud Physics, Third Edition, Butterworth-Heinemann, 1er janvier, 1989, 304 pages (ISBN 978-0-7506-3215-7 et 0-7506-3215-1).


























