Instabilité symétrique conditionnelle
L’instabilité symétrique conditionnelle[1] ou ISC (parfois appelé instabilité conditionnelle symétrique ou ICS) est une forme d'instabilité convective dans un fluide soumis à des différences de températures dans un référentiel en rotation uniforme alors qu'il est stable thermiquement (stabilité hydrostatique) dans la verticale et dynamiquement dans l'horizontal (stabilité inertielle). L'instabilité dans ce cas se manifeste seulement dans un plan incliné par rapport aux deux axes mentionnés et c'est pourquoi elle peut donner lieu à une convection dite « oblique » si une particule d'air presque saturée est déplacée latéralement et verticalement dans une zone d’ISC.
Ce concept est surtout employé en météorologie pour expliquer la formation à méso-échelle de bandes de précipitations intenses dans une région autrement stable, comme à l'avant d'un front chaud. Il est parfois connu sous son appellation anglaise de Conditional Symetric Instability (CSI) et la convection engendrée sous Slantwise Convection[2]. Le même phénomène est aussi applicable à l'océanographie[3].
Principe
Stabilité hydrostatique
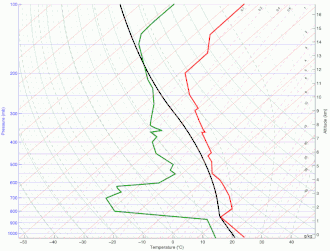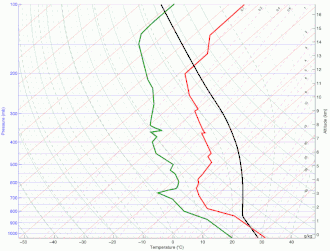
Une particule d'air se trouvant à une certaine altitude sera stable si sa température modifiée adiabatiquement lors d'une ascension est égale ou plus froide que l'environnement. De même, elle est stable si sa température est égale ou plus chaude lors d'une descente. Dans le cas où la température est égale, la particule demeurera à la nouvelle altitude, alors que dans les autres cas, elle reviendra vers son niveau initial[4].
Dans l'image de droite, la ligne jaune représente une particule soulevée dont la température demeure d'abord sous celle de l'environnement (air stable) ce qui n'entraine aucune convection. Ensuite dans l'animation, il y réchauffement réchauffement en surface et la particule soulevée reste plus chaude que l'environnement (air instable). Une mesure de la stabilité hydrostatique est de noter la variation avec la verticale de la température potentielle équivalente ()[5] :
- Si diminue avec l'altitude, on a une masse d'air instable
- Si reste le même avec l'altitude, on a une masse d'air neutre
- Si augmente avec l'altitude, on a une masse d'air stable.
Stabilité inertielle
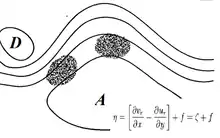
De la même façon, un déplacement latéral d'une particule d'air change son tourbillon absolu η. Ce dernier est constitué de , le paramètre de Coriolis, et de , le tourbillon géostrophique[6] :
Où :
- est la vitesse dans la direction des x ;
- est la vitesse dans la direction des y ;
- augmente en allant vers les pôles et diminue vers l'équateur ;
- varie selon le gradient de pression : positif pour une rotation anti-horaire et négatif pour une rotation horaire.
peut donc être positif, nul ou négatif selon les conditions dans lesquelles se fait le déplacement. Comme le tourbillon absolu est presque toujours positif à l’échelle synoptique, on peut considérer que l’atmosphère est stable en général pour un mouvement latéral. La stabilité inertielle n'est faible que lorsque est près de zéro. Comme est toujours positif, peut être satisfaite seulement du côté anticyclonique d’un fort maximum de courant-jet ou dans une crête barométrique en altitude, là où les dérivées des vitesses dans la direction du déplacement dans l'équation donnent une valeur importante négative[7].
En considérant la quantité de mouvement (M) d'une particule déplacée perpendiculairement au vent géotrophique[5] - [7] :
Où :
- Vg est la composante du vent géostrophique dans la direction du déplacement ;
- x est la distance déplacée dans cette direction.
La variation du moment cinétique indique alors la stabilité[5] - [7] - [8] :
- , la particule demeure alors à la nouvelle position car sa quantité de mouvement n'a pas changé ;
- , la particule revient à sa position d'origine car sa quantité de mouvement est plus grande que celle de l'environnement ;
- , la particule continue son déplacement car sa quantité de mouvement est plus petite que celle de l'environnement.
Mouvement oblique
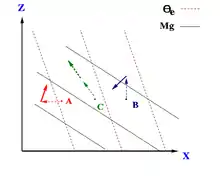
Dans certaines conditions stables hydrostatiques et inertielles, un déplacement latéral oblique peut cependant être instable lorsque la particule change de masse d'air ou de régime de vent. La figure de droite montre une telle situation. Le déplacement de la particule d'air se fait par rapport aux lignes de moment cinétique () qui augmentent de gauche à droite et de température potentielle équivalente () qui augmentent avec la hauteur.
- Déplacement latéral A
Les accélérations horizontales (vers la gauche ou la droite d’une surface ) sont dues à une augmentation/diminution de la de l’environnement dans lequel la particule se déplace. Dans ces cas, la particule accélère ou ralentit pour s’ajuster à son nouvel environnement. La particule A subit une accélération horizontale qui lui confère une flottabilité positive à mesure qu’elle se déplace vers de l’air plus froid et une décélération à mesure qu’elle se déplace vers une région de plus petite . La particule s’élève et devient éventuellement plus froide que son nouvel environnement. À ce point, elle possède une flottabilité négative et commence à descendre. Ce faisant, augmente et la particule retourne à sa position originale[7].
- Déplacement vertical B
Les mouvements verticaux dans ce cas ont pour résultat une flottabilité négative car la particule rencontre de l’air plus chaud ( augmente avec la hauteur) et une accélération horizontale à mesure qu’elle se déplace vers des surfaces de plus grande . À mesure que la particule descend, sa diminue pour s’ajuster à l’environnement et la particule revient à B[7].
- Déplacement oblique C
Seul le cas C est instable. L'accélération horizontale se combine à une perturbation verticale vers le haut et permet un déplacement oblique. En effet, la de la particule est plus grande que la de l’environnement, alors que la quantité de mouvement de la particule est inférieure à celle de l’environnement. Un déplacement oblique produit donc une flottabilité positive et une accélération dans la direction du déplacement oblique qui le renforce[7].
La condition pour avoir de l'instabilité symétrique conditionnelle dans une situation autrement stable est donc que[5] - [7] :
- la pente de soit plus grande que celle de ;
- l'air déplacé latéralement soit presque saturé.
Effets potentiels

L’ISC est habituellement encastrée dans de grandes régions de mouvement vertical ascendant. La situation idéale est un écoulement géostrophique du sud avec des vitesses de vent qui augmentent avec l'altitude. L’environnement doit aussi être bien mélangé et proche de la saturation.
Puisque l’écoulement est unidirectionnel, la composante u (est-ouest) du vent peut être posée égale à zéro, ce qui établit un écoulement symétrique perpendiculaire au gradient de température dans la masse d'air. On trouve typiquement ce type d’écoulement dans des atmosphères baroclines avec l’air froid à l’ouest[9].
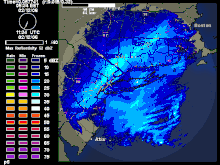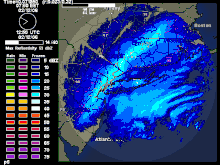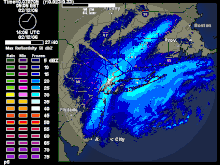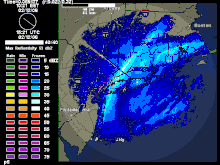
Une telle situation se retrouve dans l'image ci-contre d'un dépression frontale avec l'ISC et les bandes de neige intenses se retrouvent le long du front chaud juste à l'est du centre de pression. La zone d'ISC est associée alors à la zone de tourbillon potentiel équivalent négatif ().
Convection oblique

Si une particule est en montée dans une zone d'ISC, elle se refroidira et la vapeur d'eau condensera lors de la saturation, donnant des nuages et des précipitations par convection oblique. Par exemple, à l'avant d'un front chaud, la masse d'air est stable car l'air doux surmonte une masse froide. L’équilibre géostrophique ramène toute particule s'éloignant perpendiculairement du centre de la dépression vers celle-ci. Cependant, un déplacement oblique vers le haut par l'accélération ascensionnelle à l'échelle synoptique dans une couche d'ISC produit des bandes parallèles de fortes précipitations[9] - [10].
L'instabilité symétrique conditionnelle affecte une couche qui peut être mince ou très étendue dans la verticale, de façon identique à la convection hydrostatique. L'épaisseur de la couche détermine le rehaussement des précipitations convectives à l'intérieur d'une région autrement stratiformes[9]. Comme le mouvement s'effectue dans une zone près de la saturation, la particule reste très proche de l'adiatique humide ce qui lui donne une énergie potentielle de convection disponible limitée. La vitesse ascensionnelle dans une zone de convection oblique va donc de quelques dizaines de centimètres par seconde à quelques mètres par seconde[9].
Cela est généralement sous la limite de vitesse ascensionnelle dans un cumulonimbus qui donne de la foudre, soit 5 m/s[9]. Il est cependant possible dans noter de la foudre dans les bandes de nuages associés avec l'ISC dans[9] :
- La région de précipitation derrière un système convectif de méso-échelle ;
- La convection hivernale en raison de la tropopause plus froide et basse aidant à l'ionisation des cristaux de glace ascendants ;
- Le mur de l'œil pendant la phase d'approfondissement d'un cyclone tropical mature, bien rarement car c'est une région symétriquement neutre et généralement exempte d'activité électrique.
Les bandes de convection oblique possèdent plusieurs caractéristiques[9] :
- Elles sont parallèles ;
- Elles sont alignés parallèlement au vent thermique ;
- Elles se déplacent avec la circulation générale ;
- L'espace entre les bandes est proportionnelle à l'épaisseur de la couche d'ISC ;
Subsidence
À l'inverse, si la particule est en descente, elle se réchauffera et deviendra relativement moins saturée ce qui dissipera les nuages. La neige produite en altitude par la convection oblique va également se sublimer dans le courant descendant ce qui accélère celui-ci et peut lui donner une vitesse de descente atteignant les 20 m/s[9]. Cet effet est associé avec la descente vers le sol du courant-jet d'occlusion[11].
Notes et références
- Bureau de traduction, « Instabilité symétrique conditionnelle », Termium, Travaux publics et Services gouvernementaux Canada (consulté le )
- (en) « Slantwise convection », Meteorology Glossary, American Meteorological Society (consulté le )
- (en) « Symetric instability », Meteorology Glossary, American Meteorological Society (consulté le )
- « Instabilité convective », Glossaire météorologique, Météo-France (consulté le )
- (en) C.A. Doswell III, « CSI Physical Discussion » [archive du ], sur www.cimms.ou.edu, CIMMS (consulté le )
- « Instabilité barocline », Glossaire météorologique, Météo-France (consulté le ).
- (en) James T. Moore, « Mesoscale Processes » [ppt], UCAR, 27 novembre - 4 décembre 2001 (consulté le ), p. 10-53.
- David M. Schultz et Philip N. Schumacher, « The Use and Misuse of Conditional Symmetric Instability », National Severe Storms Laboratory, 14 décembre, 1998 (consulté le ).
- (en) David M. Schultz et Philip N. Schumacher, « The Use and Misuse of Conditional Symmetric Instability », Monthly Weather Review, AMS, vol. 127, no 12, (ISSN 1520-0493, DOI 10.1175/1520-0493(1999)127<2709:TUAMOC>2.0.CO;2, lire en ligne [PDF], consulté le ).
- (en) Theodore W. Funk et James T. Moore, « Vertical Motion Forcing Mechanisms Responsable for the Production of a Mesoscale very heavy snow band across Northern Kentucky », National Weather Service.
- (en) Geraint Vaughan, « Sting Jets » [ppt], sur eumetrain.org (consulté le ).
Liens externes
- (en) David M. Schultz et Philip N. Schumacher, « The Use and Misuse of Conditional Symmetric Instability », sur www.nssl.noaa.gov, National Severe Storms Laboratory
- (en) « Slantwise convection », Cours COMET, UCAR (consulté le ) : « Cours interactif sur la convection oblique et l’ISC qui nécessite une inscription disponible pour tous »



![\eta =\left[{\frac {\partial v_{r}}{\partial x}}-{\frac {\partial u_{r}}{\partial y}}\right]+f=\zeta +f\qquad \qquad](https://img.franco.wiki/i/29f82c531758758a7175e091407040b0b8d10325.svg)









