Tourbillon potentiel

Le tourbillon potentiel (TP) est un concept conservatif de dynamique des fluides qui décrit la valeur du tourbillon dans une masse de fluide (généralement l'air ou l'océan) dans une colonne comprise entre deux surfaces isentropes adjacentes. Un déplacement depuis une latitude standard arbitraire vers une autre, réduit ou étire l'épaisseur de la colonne afin de conserver le tourbillon potentiel et cette valeur permet ainsi d'identifier les caractéristiques de la masse et de suivre son déplacement[1].

Conservation du tourbillon potentiel menant à de la convergence et de la divergence dans le fluide.

Le tourbillon potentiel est utilisé en météorologie et en océanographie pour décrire le mouvement vertical dans l'atmosphère et l'océan. C'est un concept servant à déterminer la cyclogénèse (formation des dépressions atmosphériques le long des fronts) et dans l'analyse des flux océaniques. Par exemple, la physique du mistral dans le sud-est de la France a longtemps été mal comprise car il est contre-intuitif que le temps soit ensoleillé à Marseille avec un vent violent de nord-ouest alors qu'à Nice un vent fort d'est souffle avec de la pluie. L'explication de ce phénomène découle du théorème de conservation du tourbillon potentiel et de son importance physique.

Définition mathématique

Carl-Gustaf Rossby est le premier à définir le tourbillon potentiel en 1936[2]. Ce travail est basée sur une analyse d'une modélisation du Gulf Stream en tant qu'une couche peu profonde d'eau par rapport à son étendue horizontale. Quelques années plus tard, Hans Ertel développa le concept dans l'équation[3] :

${\rm {TP}}={\frac {1}{\rho }}(2{\vec {\Omega }}+{\vec {\nabla }}\wedge {\vec {u}})\cdot \,{\vec {\nabla }}\theta ={\frac {1}{\rho }}\,{\vec {\zeta }}\,^{a}\cdot \,{\vec {\nabla }}\theta \qquad \scriptstyle ({\text{en}}\ \mathrm {m^{2}K\ s^{-1}kg^{-1}} {\text{et une valeur de}}\ 10^{-6}\mathrm {m^{2}K\ s^{-1}kg^{-1}} {\text{est appelée une unité de TP}})$ .

Où:

$\rho$ est la densité du fluide (en kilogrammes par mètre cube) ;
${\vec {\Omega }}$ est la vitesse angulaire de rotation de la Terre à la latitude considérée ;
${\vec {u}}$ est la vitesse de déplacement d'un parcelle d'air par rapport à la Terre ;
${\vec {\zeta }}^{a}$ est le tourbillon absolu en seconde^-1. Il peut être décomposé en ses deux composantes ${\vec {\nabla }}\wedge {\vec {u}}={\vec {\zeta }}$ , le tourbillon relatif de la colonne de fluide, et $2{\vec {\Omega }}$ , le tourbillon de Coriolis à la latitude considérée (proportionnel au paramètre de Coriolis f) ;
${\vec {\nabla }}\theta$ est le gradient de température potentielle (en kelvins par mètre).

Il est possible de démontrer par la première loi de la thermodynamique et de la conservation du mouvement que le tourbillon potentiel est isentropique. Une colonne de fluide ayant un TP donné ne peut en changer que par un changement diabatique (où il y a échange de chaleur avec l'environnement) ou par friction. Le tourbillon potentiel devient donc une façon de suivre les mouvements verticaux dans une masse d'air avec température potentielle constante.

Démonstration de l'invariance du tourbillon potentiel

La démonstration est principalement basée sur la référence de Hoskins[4]. Cependant, cette référence fait l'hypothèse que l'atmosphère est barotrope ce qui n'est pas nécessaire. L'extension du domaine de validité de la preuve (aucune hypothèse d'atmosphère barotrope) est basée sur celle de Malardel[5].

On raisonne dans un référentiel galiléen. On considère un cylindre infiniment petit de base δ S et de hauteur δ h dont la base est parallèle à la surface de température potentielle.

On intègre le tourbillon sur la base du cylindre d'aire δ S. On a donc :

\int _{\delta S}{\vec {\zeta }}d{\vec {A}}=\int _{\delta S}[{\vec {\nabla }}\wedge {\vec {u}}]\cdot d{\vec {A}}

Soit $\zeta _{\theta }$ la composante pseudo-verticale dudit vecteur (perpendiculaire à la surface $\theta$ constant). On a donc :

\zeta _{\theta }\delta S=\int _{\delta S}{\vec {\zeta }}d{\vec {A}}=\int _{\delta S}[{\vec {\nabla }}\wedge {\vec {u}}]\cdot d{\vec {A}}

On utilise le théorème de Stokes. Soit $\partial \delta S$ le contour de la surface δ S. On a :

\int _{\delta S}[{\vec {\nabla }}\wedge {\vec {u}}]\cdot d{\vec {A}}=\oint _{\partial \delta S}{\vec {u}}\cdot d{\vec {l}}

On définit la circulation $\Gamma =\zeta _{\theta }\delta S$ . (on remarque que la circulation est un infiniment petit). On a donc :

\Gamma =\oint _{\partial \delta S}{\vec {u}}\cdot d{\vec {l}}

On calcule la dérivée lagrangienne de la circulation de la parcelle d'air (on la suit) :

{d\Gamma  \over dt}=\oint _{\partial \delta S}{d{\vec {u}} \over dt}\cdot d{\vec {l}}+\oint _{\partial \delta S}{\vec {u}}\cdot d{\vec {\dot {l}}}

Soit $\Psi$ le champ potentiel. On peut écrire : ${d{\vec {u}} \over dt}=-{1 \over \rho }{\vec {\nabla }}p+{\vec {\nabla }}\Psi$

On obtient donc :

{d\Gamma  \over dt}=\oint _{\partial \delta S}\left(-{1 \over \rho }{\vec {\nabla }}p+{\vec {\nabla }}\Psi \right)\cdot d{\vec {l}}+\oint _{\partial \delta S}{\vec {u}}\cdot d{\vec {\dot {l}}}

Pour rendre la formule plus claire, on remplace $d{\vec {l}}$ par $\delta {\vec {l}}$

On a donc:

{\vec {u}}\cdot d{\vec {\dot {l}}}={\vec {u}}\cdot {d\delta {\vec {l}} \over dt}

Donc,

{\vec {u}}\cdot d{\vec {\dot {l}}}={\vec {u}}\cdot {d[({\vec {x}}+\delta {\vec {l}})-{\vec {x}}] \over dt}

Donc,

{\vec {u}}\cdot d{\vec {\dot {l}}}={\vec {u}}\cdot [{\vec {u}}({\vec {x}}+\delta {\vec {l}})-{\vec {u}}({\vec {x}})]

On remarque que:

{\vec {u}}({\vec {x}}+\delta {\vec {l}})={\vec {u}}({\vec {x}})+{\partial {\vec {u}} \over \partial {\vec {x}}}\delta {\vec {l}}

Donc,

{\vec {u}}({\vec {x}}+\delta {\vec {l}})-{\vec {u}}({\vec {x}})={\vec {u}}\cdot {\partial {\vec {u}} \over \partial {\vec {x}}}

Ensuite:

{\vec {u}}\cdot {\partial {\vec {u}} \over \partial {\vec {x}}}={1 \over 2}{\vec {\nabla }}{\vec {u}}^{2}

et donc finalement,

{d\Gamma  \over dt}=\oint _{\partial \delta S}-{1 \over \rho }{\vec {\nabla }}pd{\vec {l}}+\oint _{\partial \delta S}{\vec {\nabla }}\Psi \cdot d{\vec {l}}+{1 \over 2}\oint _{\partial \delta S}({\vec {\nabla }}{\vec {u}}^{2})\cdot d{\vec {l}}

On utilise à nouveau le théorème de Stokes et pour toute application f bien définie, l'on a :

\oint _{\partial \delta S}{\vec {\nabla }}f\cdot d{\vec {l}}=\int _{\delta S}{\vec {\nabla }}\wedge {\vec {\nabla }}fdS=\int _{\delta S}{\vec {0}}d{\vec {A}}=0

. Donc,

{d\Gamma  \over dt}=\oint _{\partial \delta S}-{1 \over \rho }{\vec {\nabla }}pd{\vec {l}}+0+0

On utilise encore le théorème de Stokes. On a donc :

\oint _{\partial \delta S}-{1 \over \rho }{\vec {\nabla }}pd{\vec {l}}=-\int _{\delta S}{\vec {\nabla }}\wedge \left({1 \over \rho }{\vec {\nabla }}p\right)\cdot d{\vec {A}}

On remarque que :

{\vec {\nabla }}\wedge \left({1 \over \rho }{\vec {\nabla }}p\right)={1 \over \rho }{\vec {\nabla }}\wedge {\vec {\nabla }}p-{1 \over \rho ^{2}}{\vec {\nabla }}\rho \wedge {\vec {\nabla }}p

Le premier terme est nul et donc : ${\vec {\nabla }}\wedge \left({1 \over \rho }{\vec {\nabla }}p\right)=-{1 \over \rho ^{2}}{\vec {\nabla }}\rho \wedge {\vec {\nabla }}p$

Ainsi,

{d\Gamma  \over dt}=-\int _{\delta S}\left(-{1 \over \rho ^{2}}{\vec {\nabla }}\rho \wedge {\vec {\nabla }}p\right)\cdot d{\vec {A}}

On note la relation suivante : $d{\vec {A}}={{\vec {\nabla }}\theta \over \|{\vec {\nabla }}\theta \|}dA$ . On remplace :

{d\Gamma  \over dt}=-\int _{\delta S}\left(-{1 \over \rho ^{2}}{\vec {\nabla }}\rho \wedge {\vec {\nabla }}p\right)\cdot {{\vec {\nabla }}\theta  \over \|{\vec {\nabla }}\theta \|}dA

On introduit l'astuce de la référence [5] : on note que $\theta$ ne dépend que de p et ρ.

On a :

{\partial \theta  \over \partial x}={\partial \theta  \over \partial p}{\partial p \over \partial x}+{\partial \theta  \over \partial \rho }{\partial \rho  \over \partial x}

De même :

{\partial \theta  \over \partial y}={\partial \theta  \over \partial p}{\partial p \over \partial y}+{\partial \theta  \over \partial \rho }{\partial \rho  \over \partial y}

De même :

{\partial \theta  \over \partial z}={\partial \theta  \over \partial p}{\partial p \over \partial z}+{\partial \theta  \over \partial \rho }{\partial \rho  \over \partial z}

On obtient donc :

{\vec {\nabla }}\theta ={\partial \theta  \over \partial p}{\vec {\nabla }}p+{\partial \theta  \over \partial \rho }{\vec {\nabla }}\rho

Le produit mixte supra est donc nul. Donc,

{d\Gamma  \over dt}=-\int _{\delta S}\left(-{1 \over \rho ^{2}}{0 \over \|{\vec {\nabla }}\theta \|}\right)dA=0

ce qui démontre que $\Gamma =\zeta _{\theta }\delta S$ est constant.

La masse d'une parcelle d'air s'écrit pour un volume infiniment petit d'aire δ S et de hauteur δ h :

\delta m=\rho \delta S\delta h

où ρ est la masse volumique de l'air.

La masse de la parcelle d'air ne varie pas au cours du temps.

Donc, le ratio

{\zeta _{\theta }\delta S \over \rho \delta h\delta S}

est constant.

Donc, ${\zeta _{\theta } \over \rho \delta h}$ est constant.

On remarque que : $\|{\vec {\nabla }}\theta \|\approx {\partial \theta \over \partial z}$ et ce à une excellente précision. Donc,

\zeta _{\theta }={{\vec {\zeta }}\cdot {\vec {\nabla }}\theta  \over \|{\vec {\nabla }}\theta \|}={{\vec {\zeta }}\cdot {\vec {\nabla }}\theta  \over {\partial \theta  \over \partial z}}

Donc,

{{\vec {\zeta }}\cdot {\vec {\nabla }}\theta  \over {\partial \theta  \over \partial z}\rho \delta h}

est constant.

Comme δ h est infiniment petit, on a :

{\partial \theta  \over \partial z}\delta h=\theta (z+\delta h)-\theta (z)

Comme le processus est adiabatique, même si δ h varie au cours du temps, $\theta (z+\delta h)$ et $\theta (z)$ restent constants. Donc,

{{\vec {\zeta }}\cdot {\vec {\nabla }}\theta  \over \rho }

est constant.

Cette quantité est appelé tourbillon potentiel (ce qui peut prêter à confusion).

On notera, qu'il n'y a pas eu besoin de supposer que le fluide est incompressible ou barotrope.

Usage

Création d'un creux en aval des montagnes Rocheuses par la conservation du TP de l'air passant au-dessus de celles-ci.

En météorologie, l'une des approximations est celle de l'atmosphère barotrope où il n'y a pas de variation de température dans une masse d'air. L'équation de tourbillon barotrope est donc une façon simple de prévoir le déplacement des creux et crêtes d'onde longue à une hauteur de 500 hPa. Dans les années 1950, le premier programme de prévision numérique du temps utilisa cette équation. Cependant, c'est l'advection de tourbillon positive dans un système barocline qui crée la cyclogénèse, le développement des dépressions des latitudes moyennes, et l'advection négative qui génère les anticyclones. Elle fait partie des équations primitives atmosphériques qui sont utilisés dans les modèles modernes.

En océanographie, les tourbillons sont particulièrement étudiés pour leur capacité à conserver les propriétés de salinité et de température dans le temps au sein d'une lentille d'eau de quelques kilomètres de diamètre et de plusieurs mètres de hauteur. On peut par exemple citer les remous (« eddies » en anglais) qui sortent de la mer Méditerranée par le canal de Gibraltar et en quelques semaines/mois arrivent dans les Caraïbes. Ces tourbillons sont recherchés par les sous-marins militaires pour cacher leur signature sonar. En effet la différence de température et de salinité du tourbillon crée une interface opaque.

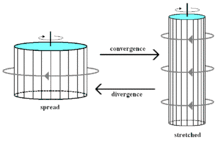
Ceci implique la conservation du tourbillon potentiel. Le TP est donc l'équivalent en dynamique des fluides de l'inertie en mécanique. Ainsi un vaste tourbillon qui tourne lentement, augmentera sa vitesse de rotation s'il est étiré verticalement par une convergence des vents en surface (changement de $\scriptstyle \zeta$ ) ou un changement de latitude (changement de $\scriptstyle f$ ). La divergence produira l'effet inverse.

Froids intenses dans le Midi de la France

Un exemple concret d'application du théorème d'invariance du tourbillon potentiel est le phénomène du mistral qui est presque toujours couplé à la dépression du golfe de Gênes qui est une dépression dynamique et qui peut engendrer des conditions météorologiques surprenantes dans le Midi de la France lorsque des vagues de froid majeures frappent le pays comme en 1709 et surtout en 1956. Il se produit alors un ciel clair à Marseille avec un mistral extrême[6] tandis que sur la Côte d'Azur, il neige abondamment[7]. La stratosphère est abaissée dans la vallée du Rhône et au nord des Alpes (et est nettement plus « chaude ») et donc $\|{\vec {\nabla }}\theta \|$ est grand. Le tourbillon ζ correspond peu ou prou au tourbillon de Coriolis. Au dessus du Golfe de Gênes, la tropopause est nettement plus élevée et la stratosphère a une température plus habituelle et en outre, la mer est plus « tiède » et donc $\|{\vec {\nabla }}\theta \|$ devient plus petit. Donc ζ devient plus grand. Comme ζ devient plus grand, une circulation cyclonique se crée au-dessus du golfe de Gênes qui engendre un retour d'est sur Nice et des chutes de neige abondantes alors qu'il fait « beau » à Marseille[8].

Notes et références

Organisation météorologique mondiale, « Tourbillon potentiel », Eumetcal, 15 mai 2016 (consulté le 7 juillet 2017).
(en) Carl-Gustaf Rossby, « Dynamic of Steady Ocean Currents in the Light of Experimental Fluid Dynamic », Papers in Physical Oceanography and Meteorology, MIT et Woods Hole Oceanographic Institition, vol. V, n^o 1,‎ 1936 (lire en ligne [PDF], consulté le 15 mai 2016).
(en) « Potential vorticity », AMS Glossary, AMS (consulté le 16 mai 2016).
Mid Latitudes, p. 177-178
Fondamentaux de météorologie, p. 665-666
Guillaume Séchet, Quel temps! : Chronique de la météo de 1900 à nos jours, Éditions Hermé, août 2005, 255 p. (ISBN 978-2-286-00897-0, lire en ligne), p. 113
A. Dugelay, « Observations générales sur la gelée de février 1956 dans les départements des Alpes-maritimes et du Var. », Revue forestière française, n^o 1,‎ janvier 1957, p. 4 (lire en ligne [PDF])
Christophe Yohia, « Genèse du Mistral par interaction barocline et advection du tourbillon potentiel », Climatologie, vol. 43,‎ 2017, p. 24 (DOI 10.4267/climatologie.1182, lire en ligne [PDF])

Bibliographie

[Midlatitudes] (en) Brian J. Hoskins et Ian N. James, Fluid Dynamics of the Midlatitude Atmosphere, John Wiley & Sons, coll. « Advancing Weather and Climate Science Series », 2014, 488 p. (ISBN 978-0-470-83369-8)
[Fondamentaux de météorologie] Sylvie Malardel, Fondamentaux de météorologie, deuxième édition, Toulouse, Cépaduès, 2009, 711 p. (ISBN 978-2-85428-851-3)

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.