Fermion lourd

Profil typique de la conductivité σ en fonction de la fréquence ω dans un matériau à fermions lourds, au-dessus de leur température de cohérence en bleu, et en-dessous de T_coh en rouge.

Les niveaux d'énergie dans les fermions lourds peuvent être étudiés par spectroscopie en faisant varier la longueur d'onde de rayonnements électromagnétiques incidents et en mesurant l'intensité réfléchie et transmise par l'échantillon[4].

Au-dessus d'une température caractéristique de cohérence, notée T_coh, les fermions lourds se comportent comme des métaux normaux, c'est-à-dire que leur réponse aux ondes électromagnétiques répond au modèle de Drude. Ils diffèrent cependant des bons métaux par un taux de diffusion élevé à haute température en raison de la forte densité de moments magnétiques localisés — au moins un électron f par maille cristalline élémentaire — qui provoquent une diffusion par effet Kondo. Il s'ensuit que la conductivité à basse fréquence et pour le courant continu est assez faible. Un roll-off de conductivité est observé à une fréquence correspondant au temps de relaxation.

En-dessous de la température de cohérence T_coh, il se produit une hybridation entre les électrons de conduction et les électrons f localisés, d'où l'augmentation de la masse effective de ces électrons. Contrairement aux isolants de Kondo, le potentiel chimique des fermions lourds se trouve dans la bande de conduction. Ceci a plusieurs conséquences sur la réponse électromagnétique des fermions lourds[2].

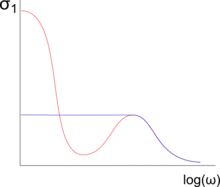
La conductivité σ peut être exprimée en fonction de la fréquence ω par ${\displaystyle \sigma (\omega )={\frac {\tau ^{*}}{1+\omega ^{2}\tau ^{*2}}}{\frac {ne^{2}}{m^{*}}}}$, où m* est la masse effective et τ* le taux de relaxation renormalisé ${\displaystyle \tau ^{*}={\frac {m^{*}}{m}}\ \tau }$[5]. L'augmentation de la masse effective conduit à l'augmentation du taux de relaxation renormalisé, d'où un roll-off plus étroit que pour les métaux normaux à très basses fréquences[5] - [6]. Le taux de relaxation le plus bas observé dans un fermion lourd à basse fréquence l'a été dans le système UPd₂Al₃ (en)[7].

La capacité thermique massique C_P des métaux conventionnels à basse température est constituée d'une partie provenant des électrons et notée C_{P, el}, et d'une partie provenant des phonons, notée C_{P, ph}. La première dépend linéairement de la température T tandis que la seconde dépend du cube T³ de la température :

${\displaystyle C_{\mathrm {P} }=C_{\mathrm {P,\ el} }+C_{\mathrm {P,\ ph} }=\gamma \ T+\beta \ T^{3}}$

avec les constantes de proportionnalité β et γ, ce dernier étant appelé constante de Sommerfeld.

À basse température, la capacité thermique massique provient essentiellement de sa fraction électronique. Celle peut être estimée à l'aide de l'approximation du gaz de Fermi par :

${\displaystyle C_{\mathrm {P,\ el} }=\gamma \ T={\frac {\pi ^{2}k_{\mathrm {B} }^{2}n}{2\epsilon _{\mathrm {F} }}}T}$

où k_B est la constante de Boltzmann, n la densité électronique, et ε_F le niveau de Fermi.

L'énergie de Fermi ε_F des électrons ayant une relation de dispersion au carré est inversement proportionnelle à la masse m de la particule :

${\displaystyle \epsilon _{\mathrm {F} }={\frac {\hbar ^{2}k_{\mathrm {F} }^{2}}{2m}}}$

où k_F est le nombre d'onde de Fermi, qui dépend de la densité électronique et est la valeur absolue du nombre d'onde du niveau d'énergie occupé de plus haute énergie. La constante de Sommerfeld γ étant inversement proportionnelle à ε_F, γ est proportionnel à la masse de la particule et, lorsque γ est élevé, le métal se comporte comme un matériau à gaz d'électrons libres dans lequel les électrons de conduction ont une masse effective thermique élevée.