Division par zéro

La division par zéro donne l'infini. Cette convention a d'ailleurs été défendue par Louis Couturat dans son livre De l'infini mathématique[1].

Cette convention est assez cohérente avec les règles de la droite réelle achevée, dans laquelle n'importe quel nombre, divisé par l'infini, donne 0.

La convention de Louis Couturat est cependant assez difficile à comprendre. Elle donne l'infini non signé comme résultat de la division de tout nombre par 0. Or, l'infini non signé est un concept encore plus difficile à saisir que « plus l'infini » et « moins l'infini ». De plus, Couturat est assez flou sur le statut qu'il faut alors donner à des expressions comme ∞ × 0.

Abbas Edalat et Peter John Potts proposèrent pour leur part d'introduire en même temps que l'infini comme inverse de zéro un second élément[2], qui lui représente les formes indéterminées, y compris celles qui apparaissent à cause de l'introduction de l'infini. En fait, ces propositions sont postérieures aux conventions informatiques.

En informatique, pour le calcul en nombres flottants, c'est un tel système qui est utilisé, en utilisant dans le calcul les éléments +∞, –∞ et NaN, ce dernier étant utilisé pour les formes indéterminées (voir #En informatique).

Si l'on emploie une telle convention, il faut se souvenir que certaines propriétés des nombres réels ne sont plus vraies dans l'ensemble formé par les nombres réels et les nouveaux éléments introduits. En effet, comme on a pour deux nombres différents n et m les égalités n/0 = ∞ et m/0 = ∞, la division n'est plus réversible par multiplication (∞ × 0 ne peut valoir simultanément n et m), et n'est donc plus définie comme son opération réciproque.

Il faut bien rappeler que par définition des nombres réels, l'infini, signé ou non, et les formes indéterminées n'en sont pas. L'ajout de ces éléments constitue donc une extension de l'ensemble des réels, comme l'est la construction des nombres complexes.

Graphe de la fonction inverse

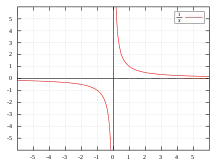
Mais en analyse, on peut essayer de donner un sens à la limite de la fonction inverse en 0, c'est-à-dire du quotient 1/x lorsque x tend vers zéro. Ainsi, si x désigne un nombre réel non nul, le quotient 1/x peut avoir une valeur absolue aussi grande qu'on veut, à condition de prendre x suffisamment proche de zéro. On écrit cela :

${\displaystyle \lim _{x\to 0}\left|{\frac {1}{x}}\right|=+\infty }$

et on dit que la valeur absolue de ce quotient admet pour limite « plus l'infini » lorsque x tend vers zéro.
Si l'on veut se passer de la valeur absolue, il faut distinguer deux cas, selon que x tend vers zéro par valeurs négatives (dans ce cas, le quotient tend vers ${\displaystyle \scriptstyle -\infty }$) ou positives (le quotient tend alors vers +∞).

On écrit : ${\displaystyle \lim _{x\to 0^{+}}{\frac {1}{x}}=+\infty }$,
et : ${\displaystyle \lim _{x\to 0^{-}}{\frac {1}{x}}=-\infty }$.

En termes vulgarisés, quand x est très petit, 1/x est très grand, ce qui peut pousser à convenir que 1/0 vaudrait l'infini. Le problème est que quand x est très petit mais inférieur à 0, 1/x devient très important en dessous de zéro. On ne peut donc définir si 1/0 vaudrait plus l'infini ou moins l'infini.

Même dans la droite réelle achevée, qui comprend –∞ et +∞ comme éléments, on ne peut donc pas définir la division par zéro (alors que l'on a, par exemple, 1/∞ = 0).

Sans autoriser la division par zéro, les nombres hyperréels admettent des nombres « infiniment petits ». Dans ce domaine des mathématiques, un nombre infinitésimal (plus petit que tout réel positif, sauf 0) a pour inverse un « infiniment grand » (plus grand que tout réel).

En algèbre, l'impossibilité de diviser tout nombre par zéro se démontre dans le cadre plus général de la théorie des anneaux.

En effet, on démontre en règle générale que l'élément neutre de la première loi de l'anneau (l'addition pour les nombres réels) est un élément absorbant pour la seconde loi (la multiplication).

• Démonstration : ${\displaystyle \forall x,y\in A,x\times y=(x+0)\times y}$ (parce que ${\displaystyle x=(x+0)}$) et ${\displaystyle (x+0)\times y=x\times y+0\times y}$ (par distributivité à droite), d'où ${\displaystyle x\times y=x\times y+0\times y}$, d'où ${\displaystyle 0=0\times y}$. De même pour l'autre côté si l'anneau n'est pas commutatif.

Donc pour tout nombre a, a × 0 = 0. Or, la division s'entend comme l'opération réciproque de la multiplication. Donc diviser par zéro reviendrait à multiplier par l'inverse de zéro. Or, zéro n'a pas d'inverse.

C'est pourquoi la division par zéro n'a non seulement pas de sens dans les ensembles de nombres usuels (entiers, réels ou complexes), mais plus généralement dans tout ensemble de nombres vérifiant les propriétés algébriques usuelles vis-à-vis de l'addition et de la multiplication (ce qu'on appelle un anneau). Il n'y a donc pas d'espoir de construire un nouvel ensemble de nombres qui donnerait un sens à l'inverse de zéro (comme celui des nombres complexes donne un sens à la racine carrée de –1), sauf si l'on accepte de perdre des propriétés essentielles du calcul algébrique usuel (notamment la distributivité de la multiplication sur l'addition).

Le problème général de la division impossible a amené en algèbre linéaire à inventer un objet conservant certaines propriétés de l'inverse : le pseudo-inverse.

Dans le cas matriciel, la définition est la suivante :

Étant donné une matrice A avec n lignes et p colonnes, son pseudo-inverse A⁺ vérifie (entre autres, on ne met que les plus simples) les conditions suivantes :

1. ${\displaystyle AA^{+}A=A\,}$ ;
2. ${\displaystyle A^{+}AA^{+}=A^{+}\,}$

Donc, en considérant les nombres comme matrices à une seule ligne et une seule colonne, le pseudo-inverse de 0 est 0.

Bien entendu, la notion de pseudo-inverse est beaucoup plus importante pour les matrices de taille supérieure. La définition d'un nouvel objet ne se justifierait pas pour donner seulement une réponse à la division par zéro pour les nombres réels.

En analyse, dans certains cas, il est possible de calculer la limite d'un quotient dont le dénominateur est une suite ou une fonction de limite nulle.

Par exemple, un cas évident est celui de la fonction ${\displaystyle f:x\longmapsto {\frac {x^{2}}{x}}}$. En principe, on devrait dire que ƒ(0) ne peut être calculé car implique une division par 0. Mais pour tout x autre que 0, on peut simplifier l'expression en ƒ(x) = x. Il est alors évident qu'on peut écrire ƒ(0) = 0 en tant que limite (valeur dont ƒ(x) devient « infiniment proche » quand x devient « infiniment proche » de 0, pour donner une idée du concept).

Bien entendu, le problème n'apparaît pas forcément en approchant la valeur 0 pour l'argument de la fonction. Par exemple, pour la fonction ${\displaystyle g:x\longmapsto {\frac {1}{x-3}}}$, c'est quand x vaut 3 qu'on a un problème de type « division par zéro ».

Suivant les expressions que l'on trouve au numérateur et au dénominateur, une expression comprenant une division par zéro peut avoir pour limite 0, un autre nombre, +∞ (plus l'infini), -∞, ou ne pas avoir de limite. Quelques exemples :

• ${\displaystyle f_{1}:x\longmapsto {\frac {x^{2}}{x}}}$ a 0 pour limite en 0 (déjà vu)
• ${\displaystyle f_{2}:x\longmapsto {\frac {\cos(x)-1}{x^{2}}}}$ a ${\displaystyle -{\frac {1}{2}}}$ pour limite en 0 (exercice courant pour étudiants en mathématiques ; utilise le développement limité)
• ${\displaystyle f_{3}:x\longmapsto {\frac {1}{x^{2}}}}$ a ${\displaystyle +\infty }$ comme limite en 0
• ${\displaystyle f_{4}:x\longmapsto \sin(1/x)}$ n'a pas de limite en 0

Dans les pseudo-démonstration d'égalité entre nombres, la méthode la plus courante consiste à démontrer que x = y, alors que c'est trivialement faux (exemple : x = 1, y = 2) en démontrant en fait que 0 × x = 0 × y (ce qui, on l'a dit plus haut, est vrai pour tous les nombres), puis en divisant par zéro des deux côtés pour simplifier (il est vrai que z × x = z × y implique que x = y pour tout nombre z autre que 0).

L'astuce consiste à compliquer les expressions de telles manières qu'on effectue la « simplification par zéro » en divisant par une expression si compliquée que le lecteur ne s'aperçoit pas qu'elle vaut 0.

Le docteur en mathématiques Jesper Carlström a fait l'inventaire des méthodes proposées pour étendre les ensembles mathématiques en autorisant la division par zéro. En généralisant les constructions précédemment proposées, il obtient une structure appelée wheel, c'est-à-dire « roue », allusion au fait que cette structure s'obtient en complétant un anneau.

Comme déjà dit, l'ensemble autorisant la division par zéro n'est même plus un anneau. Et dans cet ensemble, si l'égalité x – x = 0 × x² reste vraie, cela ne signifie pas forcément que x – x = 0[3].

Le professeur d'informatique James Anderson proposa pour sa part d'ajouter les deux infinis et un nouveau nombre appelé nullity (qu'on obtient, par exemple, en faisant 0/0) pour autoriser la division par zéro dans tous les cas. Les critiques remarquèrent que cela revenait à peu près au même que la convention déjà utilisée en informatique (voir plus bas), à cela près que la réponse des ordinateurs pour une forme indéterminée, NaN (ce qui signifie : « pas un nombre ») est appelée un nombre, et que quelques-unes de ses propriétés conventionnelles changent[4].

Pour comprendre les raisons d'une division par zéro, il faut mentionner la notion d'« annulation catastrophique » (Catastrophic cancellation). Pour des nombres enregistrés dans la mémoire d'un ordinateur, on utilise généralement la représentation en virgule flottante. Or, cela signifie que les nombres ne peuvent être connus qu'avec une précision relative limitée. L'annulation catastrophique est la soustraction de deux nombres qui ne sont pas formellement égaux, mais le sont dans la limite de la précision utilisée[7].

Donc, bien que d'un pur point de vue mathématique l'exponentielle d'un nombre non nul soit différente de 1, en informatique 1/(exp(x)-1) provoquera une division par zéro, non seulement si x est nul, mais aussi quand x est non nul mais que exp(x) est un nombre trop peu différent de 1 pour être distingué en représentation flottante. Or en virgule flottante, la précision est relative. Ce qui signifie que ce format permet de représenter des nombres très petits (par exemple, le format « simple précision » permet de représenter des valeurs de l'ordre de 10^-38), mais qu'il ne peut pas représenter une différence par rapport à 1 aussi faible (toujours en « simple précision », le plus faible écart à 1 représentable est de l'ordre de 10^-8).