Dépouillement d'une courbe
En sciences expérimentales, le relevé de données se représente fréquemment sur un graphique et prend alors souvent la forme d'une courbe. Le dépouillement de la courbe est l'opération qui consiste à extraire des informations de cette courbe ; l'information ne provient pas des valeurs individuelles des points, mais de leur organisation, de la forme de la courbe.
Lorsque cette courbe est un spectre, on parle de dépouillement d'un spectre.
Origine de la courbe
Les valeurs peuvent être relevées individuellement (mesure manuelle, lecture sur un appareil, acquisition automatique) et placées sur un graphique (points placés à la main sur du papier millimétré, ou valeurs entrées dans un tableur ou un logiciel de représentation de données), ou bien le graphique peut être directement issu de l'acquisition (tracé sur une table traçante, acquisition automatique générant directement le graphique).
Le traitement peut être manuel, « à la règle et au crayon », ou informatisé. Lorsque la courbe est une courbe analogique (tracée par une table traçante), il est possible de numériser la courbe. Cela peut se faire à l'aide d'un scanner puis d'un logiciel de traitement d'image (pour reconnaître les axes et la courbe), ou bien à l'aide d'une table de numérisation (sorte de souris transparente, le clic permettant d'enregistrer le point).
Traitement manuel
Régression
Dans certains cas, on sait que les valeurs doivent suivre une loi mathématique. Si cette loi est suffisamment simple, on peut en déterminer les paramètres à partir des points : c'est la régression. Le cas le plus simple est celui d'une loi affine (polynôme du premier degré), on parle alors de régression linéaire.
Une fois cette loi déterminée, on peut « remplacer » les points expérimentaux par cette loi, ce qui permet d'utiliser un traitement mathématique et remplacer les techniques ci-dessous. L'erreur commise en faisant cette substitution est estimée par la moyenne quadratique de l'écart entre les points et la loi, que l'on nomme écart quadratique.
À l'inverse, les techniques ci-dessous peuvent permettre de déterminer les paramètres de la loi.
Lorsque la loi est un du type ( étant un nombre réel), on peut utiliser une échelle logarithmique pour l'abscisse et l'ordonnée. On a alors une droite, et la pente de la droite donne la puissance de la loi :
La régression linéaire est normalement un traitement statistique des valeurs, mais on peut, lorsque les points sont « bien alignés », effectuer un tracé à la règle. Cependant, si cette technique est simple, elle ne permet pas de déterminer l'écart quadratique entre les points et la droite.
On sait que par points, on peut faire passer un polynôme de degré (interpolation polynomiale). Il pourrait être tentant de définir un tel polynôme pour avoir une fonction mathématique « exacte ». C'est cependant en général une mauvaise idée, car cela ne prend pas en compte la dispersion des résultats et les barres d'erreur, on obtient donc certes un écart quadratique nul, mais des résultats qui ne correspondent finalement pas à l'expérience.
Lorsque la courbe n'est pas continue ou pas dérivable, il peut être intéressant de la modéliser par partie, c'est-à-dire d'utiliser différentes fonctions selon l'intervalle de valeurs.
Lissage
En mathématiques, on peut définir des fonctions nulle part continues, ou bien continues mais nulle part dérivables. Toutefois, ces fonctions ne sont d'aucune utilité en sciences expérimentales ; toutes les courbes peuvent être considérées comme continues et dérivables, du moins par partie. Il est donc légitime d'effectuer un lissage au lieu de se contenter de relier les points par une ligne brisée.
En général, on reporte l'erreur de mesure sous la forme de barres sur le graphique, les barres d'erreur. Le lissage consiste à faire un tracé à main levée passant à l'intérieur de ces barres d'erreur.
On utilise ici le « pouvoir intégrateur » du cerveau humain.
Asymptote
Une asymptote est une valeur limite vers laquelle tend la courbe, mais qui n'est en général pas atteinte. On peut prendre par exemple le cas en électrocinétique de la tension aux bornes d'un condensateur lors de sa charge sous une tension continue.
Pour une asymptote à l'infini, on effectue une mesure sur une grande plage de valeurs (de longue durée si l'abscisse est le temps), et on prend la valeur maximale atteinte, lorsque la courbe semble présenter un plateau.
Dans le cas d'une asymptote verticale à une abscisse donnée, on encadre le point : on situe approximativement la position de cette asymptote, et l'on effectue des relevés de points supplémentaires entre les deux points encadrant cette valeur ; il s'agit d'un sur-échantillonnage local. On peut éventuellement procéder par dichotomie.
Point d'inflexion
Un point d'inflexion se repère à l'œil nu ; la direction de la tangente est en général assez claire. Pour déterminer sa position, on place la règle dans la direction de la tangente, et on la fait glisser jusqu'à ce qu'elle affleure la courbe ; on trace ainsi la tangente.
Si la dérivée évolue lentement (la valeur absolue de la dérivée seconde est faible), la courbe présente une partie quasiment droite ce qui permet de déterminer facilement la direction de la tangente ; mais alors, il est plus difficile de placer précisément le point d'intersection entre la tangente et la courbe, puisqu'un petit écart sur la position de la tangente entraîne un grand écart sur la position du point.
Dérivée et tangente
La tangente en un point peut être déterminée par la droite passant par le point précédent et le point suivant (corde de la courbe) : on trace la corde entre le point et le point , et on trace la parallèle à cette droite au point . Cette technique est d'autant plus juste que les points sont équitablement espacés sur la courbe (en abscisse curviligne). On prend pour dérivée la pente de la droite.
On peut justifier cette approximation par le théorème des accroissements finis, disant que
- Si une fonction est dérivable sur l'intervalle , il existe un point entre et tel que la dérivée est égale au taux de variation entre et .
On suppose donc que ledit point est proche du point .
On voit également que cela revient assimiler la dérivée au taux de variation, ce qui est justifié par la définition de la dérivée (limite du taux de variation lorsque les points se rapprochent).
Si les points présentent une dispersion importante (voir les articles Erreur (métrologie) et Rapport signal sur bruit), on a tout intérêt à lisser la courbe avant de déterminer la dérivée.
Travail sur les pics
Dans un certain nombre de cas, la courbe présente des pics, des « courbes en cloche ». L'information pertinente peut provenir de la position, de la hauteur, de la largeur ou de la surface du pic.
En théorie, un pic est une courbe s'étendant à l'infini des deux côtés, mais se rapprochant « assez vite » de la ligne de fond. Dans la pratique, on ne considère souvent que les points se détachant notablement de la ligne de fond (voir l'article Limite de détection).
Un des grands problèmes est celui de la superposition de deux pics, lorsque la distance entre deux pics est faible par rapport à leur largeur.
Sommet d'un pic
Le pic se superpose en général à une courbe que l'on appelle le fond.
Au sens strict, le sommet du pic est le point le plus haut. Si l'on a la liste de valeurs, il suffit de prendre la plus élevée. Toutefois, lorsque les points présentent des oscillations importantes (bruit), le point maximal n'est pas forcément représentatif du pic. On peut alors faire un lissage, ou bien faire une régression avec une fonction courbe, par exemple une parabole, avec quelques points autour du point maximum, on prend alors le sommet de la parabole.
Lorsque l'on a une courbe tracée, on utilise le fait qu'au maximum, la tangente est horizontale. On fait alors glisser la règle parallèlement à l'axe des abscisses, et on regarde le moment où la règle atteint le sommet.
Si le pic est symétrique (que le fond soit horizontal ou pas), on peut aussi utiliser le milieu du segment joignant les points d'inflexion sur les flancs du pic, ce que l'on appelle le « milieu de la corde ».
Graphiquement, on signale le sommet par une double-flèche tangente à la courbe.
Le sommet déterminé indique donc la position du pic, mais aussi sa hauteur. On distingue :
- la hauteur brute : c'est l'ordonnée du point ;
- la hauteur nette : c'est l'ordonnée du point moins l'ordonnée de la ligne de fond à la même abscisse.
C'est souvent la hauteur nette qui est intéressante
Largeur d'un pic
Pour déterminer la largeur d'un pic, on utilise en général la largeur à mi-hauteur (en anglais : full width at half maximum, FWHM).
Pour cela,
- on trace une droite verticale passant par le sommet du pic,
- on détermine le milieu du segment entre le sommet et le fond ;
- on trace une droite parallèle au fond.
La largeur à mi-hauteur est la largeur du segment que forme l'intersection de cette droite avec la courbe.
On peut également définir la largeur du pic par la longueur du segment joignant les points d'inflexion des flancs.
Enfin, si l'on dispose des valeurs des points, on peut utiliser l'écart type expérimental s, c'est-à-dire la racine carrée de la variance empirique des points du pic
où est la position du sommet.
Surface d'un pic
Si l'on veut juste comparer les surfaces des pics entre eux, on peut se contenter d'estimer la surface par le produit hauteur × largeur, en supposant que les formes des pics suivent une même fonction mathématique.
La surface du pic peut être déterminée, si l'on dispose des valeurs des points, à l'aide d'une méthode d'intégration numérique telle que la méthode des trapèzes ou de Simpson par exemple.
Une ancienne méthode consiste à découper le pic avec des ciseaux et à le peser avec une balance suffisamment précise. L'unité de surface est le produit des unités des axes. Pour avoir la surface dans cette unité, il faut diviser la masse par le grammage du papier (masse surfacique, en général indiquée en g/m²), puis de convertir cette valeur (en m²) avec les échelles des axes.On distingue :
- la surface brute : on découpe le pic jusqu'à l'axe des abscisses (ou on multiplie la hauteur brute par la largeur) ;
- la surface nette : on découpe le pic jusqu'à la ligne de fond (ou on multiplie la hauteur nette par la largeur).
Traitement automatisé
Lorsque les points sont relevés sous forme de valeur, il est alors intéressant de faire les traitements par informatique.
Régression
La régression, appelée en anglais profile fitting (ajustement de profil), peut s'effectuer avec tout type de fonction.
La régression permet de résoudre de manière efficace les problèmes de superposition de pics.
Travail sur les pics
On peut, comme pour le traitement manuel, prendre un fond linéaire en définissant des positions fixes. Mais on peut aussi ajuster un polynôme sur la courbe que l'on obtient lorsque l'on enlève les pics.
On peut ajuster le pic par régression (par exemple fonction gaussienne, pseudo-fonction de Voigt…) ; dans ce cas-là, les paramètres du pic peuvent être déduits des paramètres de la fonction.
Position et hauteur du pic
La position du sommet peut être déterminée en ajustant une parabole aux points situés autour du point le plus haut.
Si le pic est symétrique, on peut aussi utiliser la moyenne pondérée m des points :
pour les N points constituant le pic.
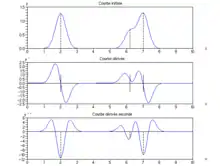
On peut également déterminer la position du sommet par la dérivée, qui présente une forme caractéristique pic positif-pic négatif et passe par zéro à l'endroit du sommet, ou bien par la dérivée seconde qui présente alors un minimum local. L'utilisation de la dérivée seconde permet de prendre en compte la superposition de deux pics, lorsqu'un des pics apparaît comme un épaulement de l'autre : à cet endroit, la dérivée ne s'annule pas puisque la tangente n'est pas horizontale ; cela revient à détecter les extrema de courbure. Les inversions de courbure, les points d'inflexion, se détectent également très bien : ce sont les intersections de la dérivée seconde avec l'axe y'' = 0.
La dérivation a intérêt à se faire sur la courbe lissée : en effet, le bruit aléatoire consistant en des variations d'un point sur l'autre, il introduit une forte perturbation de la dérivation (le δx étant petit, le taux de variation est très grand). Si l'on utilise l'algorithme de Savitzky-Golay, on peut utiliser la dérivée du polynôme au milieu du segment glissant.
Surface et largeur du pic
La surface, nette ou brute, peut être déterminée par intégration numérique.
On peut alors définir une autre largeur : la largeur intégrale, qui est le rapport de la surface nette sur la hauteur nette. C'est la largeur d'un rectangle qui aurait la même surface nette et la même hauteur nette que le pic.
Déconvolution de pics
Un pic correspond à un phénomène physique. Lorsque des phénomènes génèrent des pics proches, ceux-ci peuvent se recouvrir ; on parle parfois d'interférence. Voir aussi l'article Résolution (optique).
Si l'on a un modèle mathématique pour la forme des pics, on peut les séparer. On parle de désommation, ou encore de déconvolution.
Dans d'autre cas, la forme du pic dépend de plusieurs paramètres. Le pic est alors la somme ou le produit de convolution de fonctions élémentaires, la forme de chaque fonction dépendant des paramètres. L'opération permettant de décomposer les pics en fonctions élémentaires porte aussi le nom de déconvolution.
Voir aussi
Bibliographie
- (en) Chao Yang, Zengyou He et Weichuan Yu, « Comparison of public peak detection algorithms for MALDI mass spectrometry data analysis », BMC Bioinformatics, vol. 10, no 4, (DOI 10.1186/1471-2105-10-4, lire en ligne)







![{\displaystyle ]a;b[}](https://img.franco.wiki/i/5876eb751b77c77759e1cd71ccc0cf532d76b025.svg)




